1.实验目的：

比较同一问题，采用不同策略设计不同算法，分析和比较算法的性能。

2.实验内容：

自学第10章的10.1.1至10.1.3, 总结分析编程实现简单算法、分治法和动态规划算法的理论复杂度，编程实现这些算法。

3.实验要求：

并对一组数据测试实际运行时间，算法实际运行时间检测实际运行时间与理论分析是否一致。

$\square$ 基础性实验 $\square$ 综合性实验 $⊠$ 设计性实验

---

实验报告正文

---

实验报告正文

一、问题分析（模型、算法设计和正确性证明等）

​ 简单算法（暴力枚举）

枚举序列子段起点，延长该子段直到序列末尾，在所有子段的求和的结果中取最大值即为所求。

​ 分治算法

从序列中间将序列分为两个子序列，则所求子段有以下三种情形：

1. 和最大子段是左子序列的子段；
2. 和最大子段是右子序列的子段；
3. 和最大子段的左子段是左子序列的子段，右子段是右子序列的子段。

对于情形1和2，可由递归求得，对于情形3，从左右子序列的分割点开始分别往左右遍历，取最大值求和即为和最大子段。

​ 动态规划

设$f[i]$表示前$i$个元素的最大子段和且一定取第$i$个元素a[i]，换而言之，$f[i]$是以a[i]结尾的子段能取到的最大值，对于$a[i]$：

当$f[i-1]\le 0$时，若把$a[i]$加入到当前和最大子段中有$f[i]=a[i]+f[i-1]\le a[i]$，故此时应把$a[i]$作为新的子段开端（此时子段中只有$a[i]$），即令f[i]=a[i]；

当$f[i-1]>0$时，有$f[i-1]+a[i]>a[i]$，故$f[i]=f[i-1]+a[i]$.

最后只需遍历所有$f[i]$取最大值即可。

二、算法设计复杂度分析（伪代码，不要粘贴源码）

时间复杂度：$T(n)\in \theta (n^2)$

空间复杂度：$S(n)\in \theta (n)$

时间复杂度：$T(n)\in \theta (n\log (n))$

空间复杂度：$S(n)\in \theta (n)$

时间复杂度：$T(n)\in O(n)$

空间复杂度：$S(n)\in O(n)$

三、实验结果记录和分析（测试向量上的测试结果、运行时间）

问题规模	计算结果	BF用时	DC用时	DP用时
50	49975	0.0066ms	0.0033ms	0.0008ms
100	91590	0.012ms	0.0058ms	0.0005ms
500	155389	0.269ms	0.0277ms	0.0016ms
1000	414102	1.0693ms	0.0566ms	0.0033ms
5000	838211	26.5556ms	0.2922ms	0.0127ms
10000	500018	107.681ms	0.886ms	0.0407ms
50000	985444	2715.4ms	3.6782ms	0.1141ms
100000	4312292	10654ms	6.7081ms	0.4336ms
500000	4545027	268872ms	35.0238ms	1.1395ms
1000000	14407453	1.1011e+06ms	74.0568ms	2.302ms

简单算法用时曲线：

分治算法用时曲线：

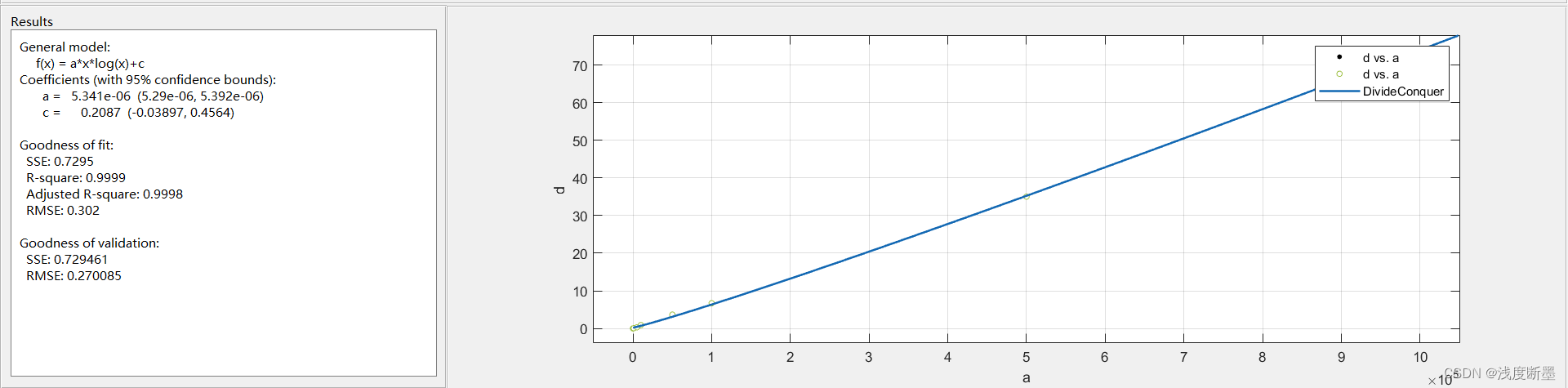
动态规划算法用时曲线：

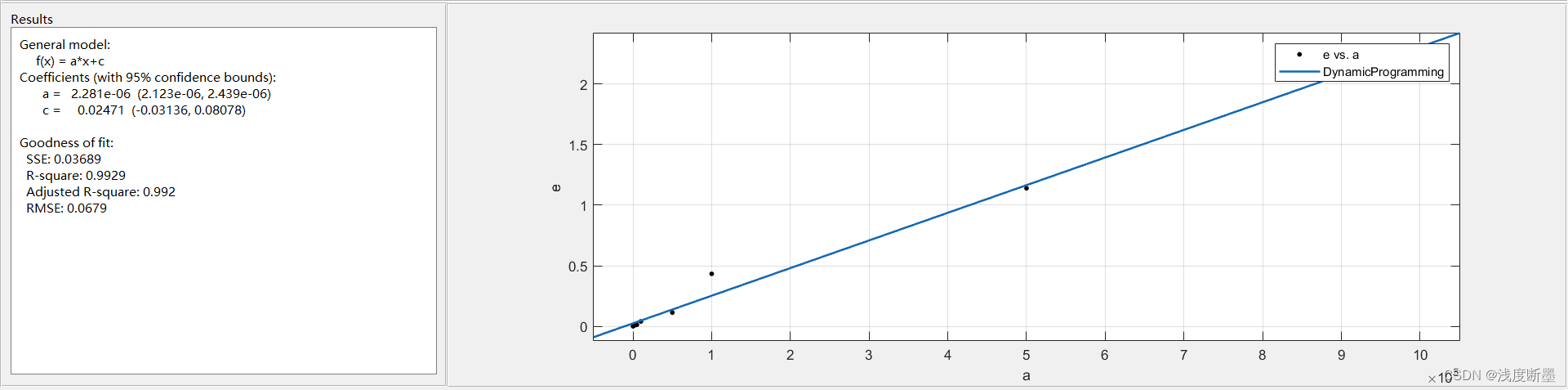
四、总结（可描述出现的问题和解决方法、经验和反思等）

三种算法在解决这个问题时都考虑到固定某一元素一定在和最大子段中，然后通过遍历、分治、动态规划的方法求解最大值。在BF算法中，固定了和最大子段的起点，分支算法固定了子段的中点，而DP算法固定了子段末尾。区别在于BF算法枚举$n$次起点，每次需要$n-i$次求和，分治算法枚举$\log n$次固定点，每次遍历加和需要$n$次，动态规划算法枚举$n$次固定点，但是每次枚举时根据之前的结果就可立刻判断最大值。