6.1.1 欧拉方法

欧拉方法是一种数值解常微分方程（ODE）的方法，可以用于近似求解给定的初值问题。它是以欧拉命名的瑞士数学家莱昂哈德·欧拉所发明的，因此得名。

欧拉方法的基本思路是将连续的常微分方程转化为离散的形式。具体而言，我们将自变量$t$的区间[t_0,t_n]等分成n个子区间，每个子区间长度为h=\frac{t_n-t_0}{n}。然后，我们选择一个起始点t_0和对应的初值y_0，并从t_0开始，使用欧拉方法逐步计算出t_1,t_2,\ldots,t_n处的近似解y_1,y_2,\ldots,y_n，直到达到目标终点t_n为止。

欧拉方法的具体实现是基于以下公式：

其中，f(t,y)是给定的常微分方程，y_i是在t_i处的近似解，h是步长，通常设置为常数。这个公式表示的是，通过使用f(t_i,y_i)来估计在t_i处的斜率，我们可以得到下一个近似解y_{i+1}，即将当前近似解y_i沿着斜率方向向前推进一个步长h。

欧拉方法是一种比较简单和直观的数值求解方法，但它也有一些缺点。例如，欧拉方法的误差通常会随着步长h的减小而减小，但这种减小速度是线性的，而不是二次或更高阶的。此外，欧拉方法在求解具有较大振荡或非线性的问题时，可能会导致数值解的不稳定性。因此，有时候需要使用更高阶的数值求解方法，例如改进欧拉方法或龙格-库塔方法，以提高求解精度和稳定性。

我的理解：

可以通过一个具体的例子来理解欧拉方法。

假设我们有一个简单的常微分方程：

其中，k是一个常数，y是未知函数。

我们希望使用欧拉方法求解这个方程。首先，我们需要将自变量t的区间[t_0,t_n]等分成n个子区间，每个子区间长度为h=\frac{t_n-t_0}{n}。然后，我们选择一个起始点$t_0$和对应的初值$y_0$。在这个例子中，我们可以选择t_0=0，y_0=1。

接下来，我们可以使用欧拉方法逐步计算出t_1,t_2,\ldots,t_n处的近似解y_1,y_2,\ldots,y_n。具体而言，我们可以使用欧拉方法的公式：

将它应用于我们的例子中，得到：

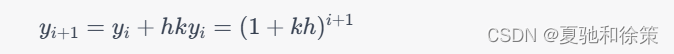
其中，i=0,1,2,\ldots,n-1。这个公式表示的是，通过使用f(t_i,y_i)=ky_i来估计在t_i处的斜率，我们可以得到下一个近似解y_{i+1}，即将当前近似解y_i沿着斜率方向向前推进一个步长h。

通过计算，我们可以得到以下结果：

i	t_i	y_i
0	0	1
1	h	1+kh
2	2h	(1+kh)^2
\cdots	\cdots	\cdots
n	nh	(1+kh)^n

这个表格显示了在$n$个子区间中，每个子区间的近似解。我们可以看到，在每个子区间内，近似解按指数级别增长。这是因为我们的方程是一个指数增长的函数，欧拉方法使用常数斜率估计了这个增长，因此在每个子区间内的近似解也呈指数增长。

当然，这个例子是非常简单的。在实际的应用中，我们通常会遇到更加复杂的常微分方程，需要使用更加高级的数值方法来求解。但是，欧拉方法作为最基础、最简单的数值方法，可以为我们提供一个初步的了解。

1.2 欧拉公式的局部截断误差与精度分析

欧拉方法的局部截断误差是指在每个步骤中，欧拉方法计算得到的数值解与真实解之间的差距。具体而言，如果我们使用欧拉方法计算出的数值解为$y_i$，而真实解为$y(t_i)$，那么局部截断误差为：

也就是说，局部截断误差是在每个步骤中欧拉方法未能精确计算出下一个点的误差。

欧拉方法的精度分析可以通过比较局部截断误差与步长$h$的关系来进行。具体而言，我们可以使用泰勒展开式将真实解表示为：

这里$O(h^3)$表示高阶无穷小，即在$h$趋近于0时，比$h^3$更小的项。将欧拉方法的数值解代入上式，并使用欧拉方法的定义，我们可以得到：

将上式代入局部截断误差的定义，我们可以得到：

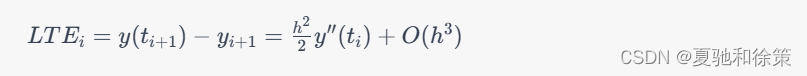
也就是说，欧拉方法的局部截断误差是二阶无穷小，与步长$h^2$成正比。因此，欧拉方法的全局误差与步长$h$成线性关系，即：

这表明欧拉方法是一种一阶精度的数值方法。如果我们想要提高数值解的精度，可以选择使用更高阶的数值方法，如改进欧拉方法或龙格-库塔方法等。

定义2 我的理解：

在数值求解常微分方程的过程中，我们希望得到一个与真实解足够接近的数值解。一般来说，我们认为一个数值方法的精度与其阶数有关。p阶方法是指一种数值方法，它在每个步骤中的误差与步长$h$的p次方成正比，也就是说，它的全局误差与步长$h^{p+1}$成正比。

具体来说，假设我们使用一个p阶方法来求解方程$y'=f(t,y)$，在第$i$个步骤中，我们使用这个方法计算得到数值解$y_{i}$，真实解为$y(t_i)$。那么这个方法在当前步骤中的局部截断误差为$LTE_i = O(h^{p+1})$。因此，该方法在整个时间区间上的全局误差为$O(h^p)$，即：