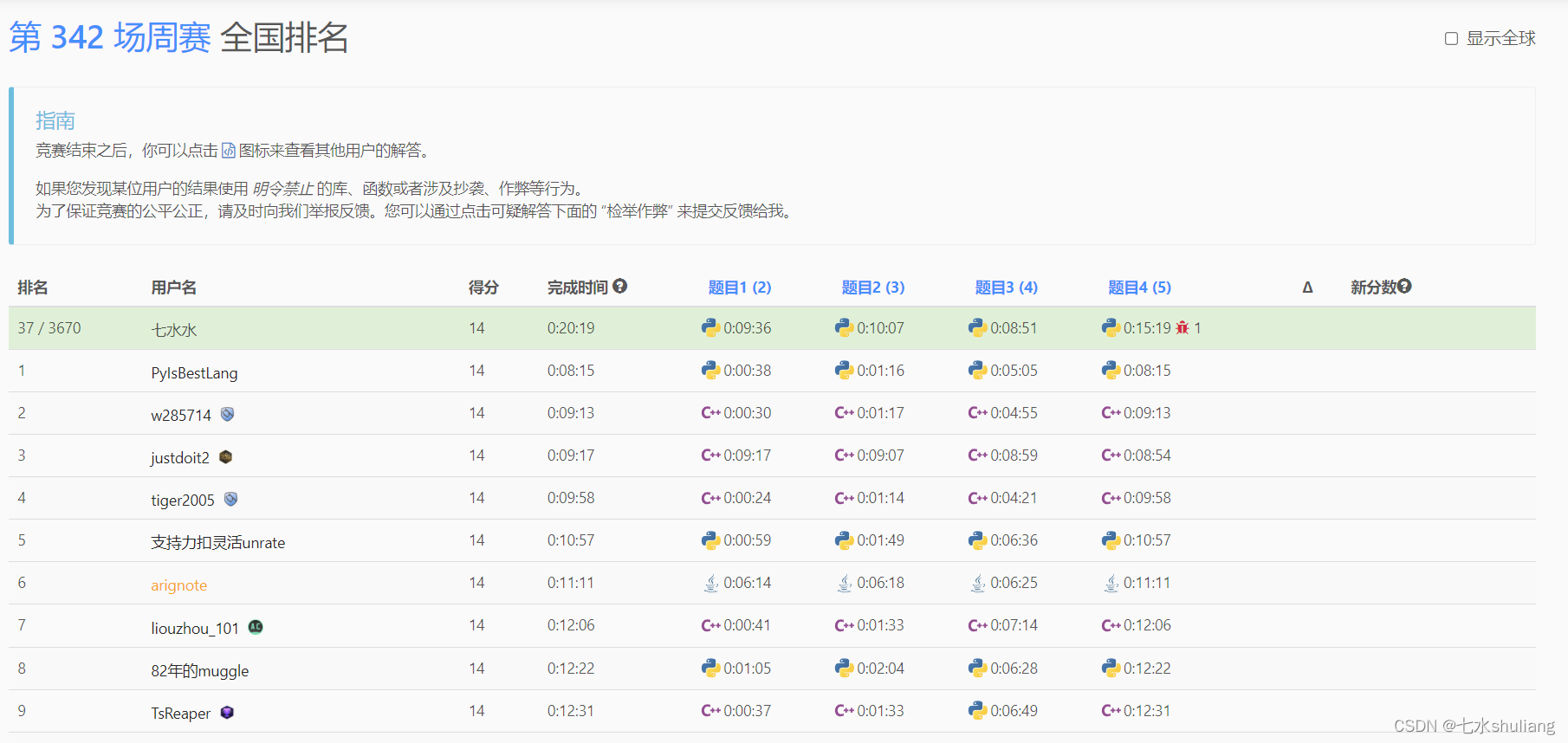
一、本周周赛总结

• easy局。
• T1 模拟。
• T2 模拟。
• T3 SortedList爽题。
• T4 暴力gcd/st+二分。
  

二、 6387. 计算列车到站时间

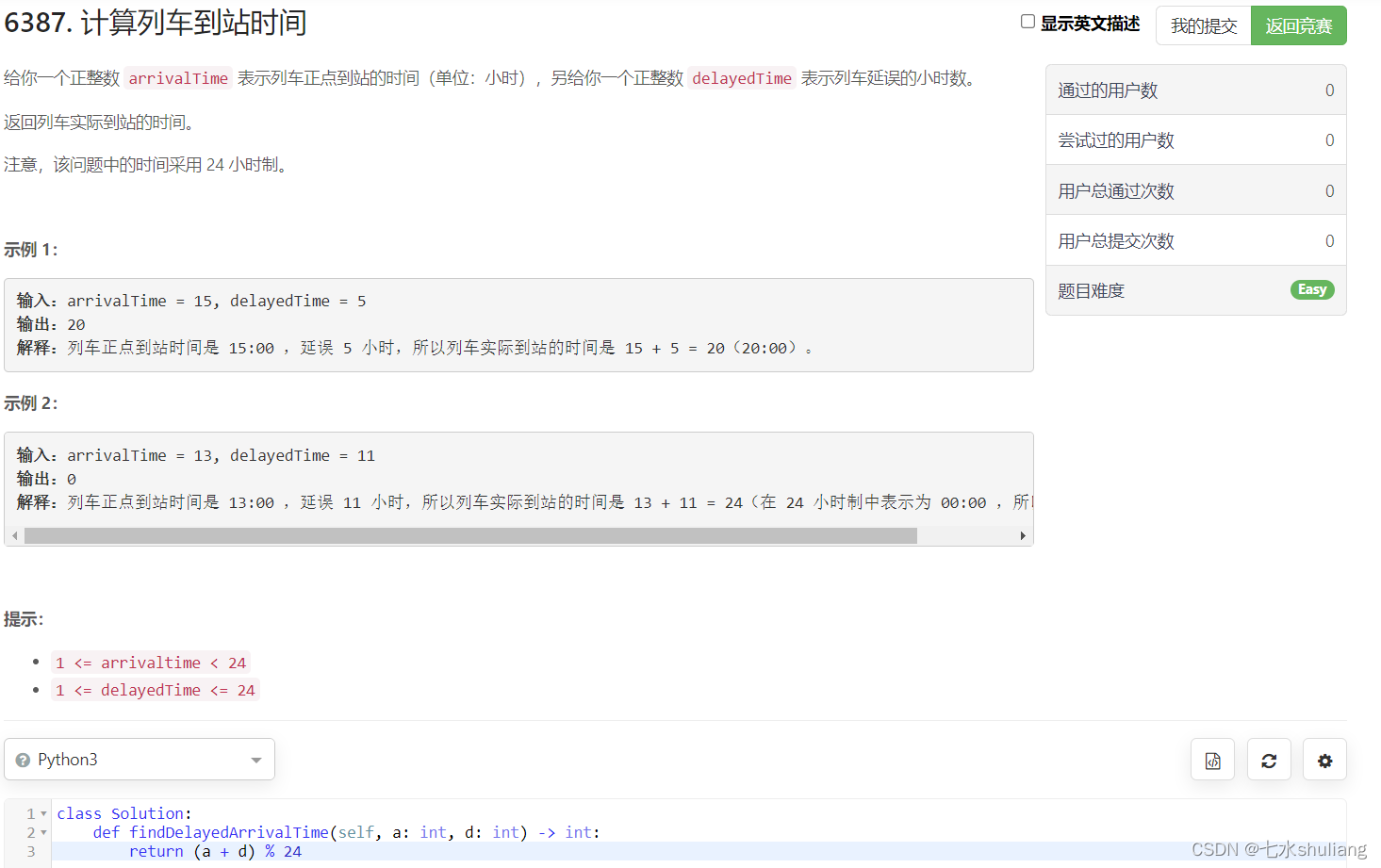
链接: 6387. 计算列车到站时间

1. 题目描述

2. 思路分析

按题意模拟即可。

3. 代码实现

class Solution:
    def findDelayedArrivalTime(self, a: int, d: int) -> int:
        return (a + d) % 24 

三、6391. 倍数求和

链接: 6391. 倍数求和

1. 题目描述

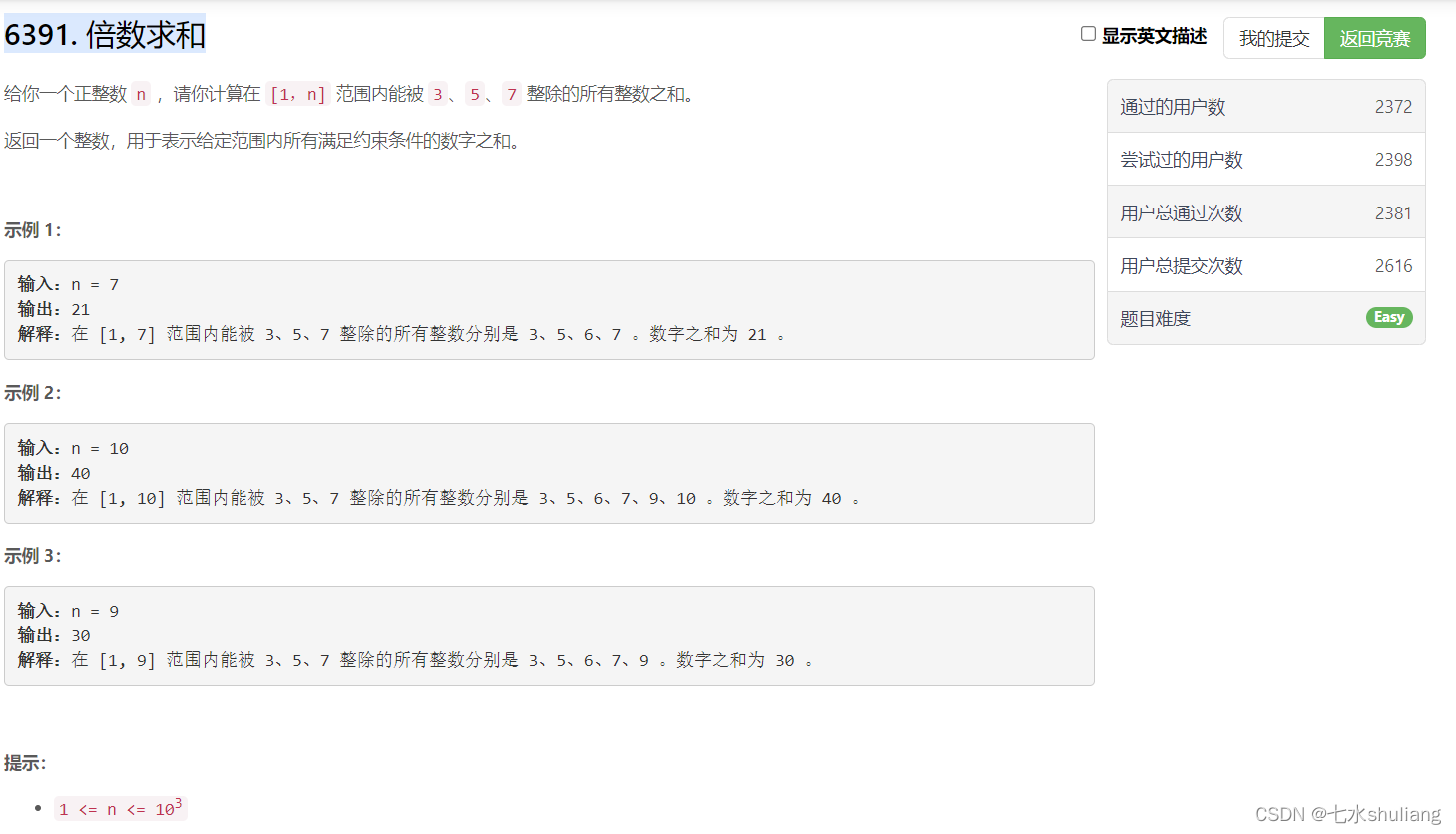
2. 思路分析

贴模板。

• 都乘到一起找质因数就是分别找质因数然后去重，因此用set记录并集即可。

3. 代码实现

class Solution:
    def sumOfMultiples(self, p: int) -> int:
        ans = 0  # 
        for i in range(1, p + 1):
            if i % 3 == 0 or    i % 5 == 0 or i % 7 == 0:
                ans += i
        return ans

四、6390. 滑动子数组的美丽值

链接: 6390. 滑动子数组的美丽值

1. 题目描述

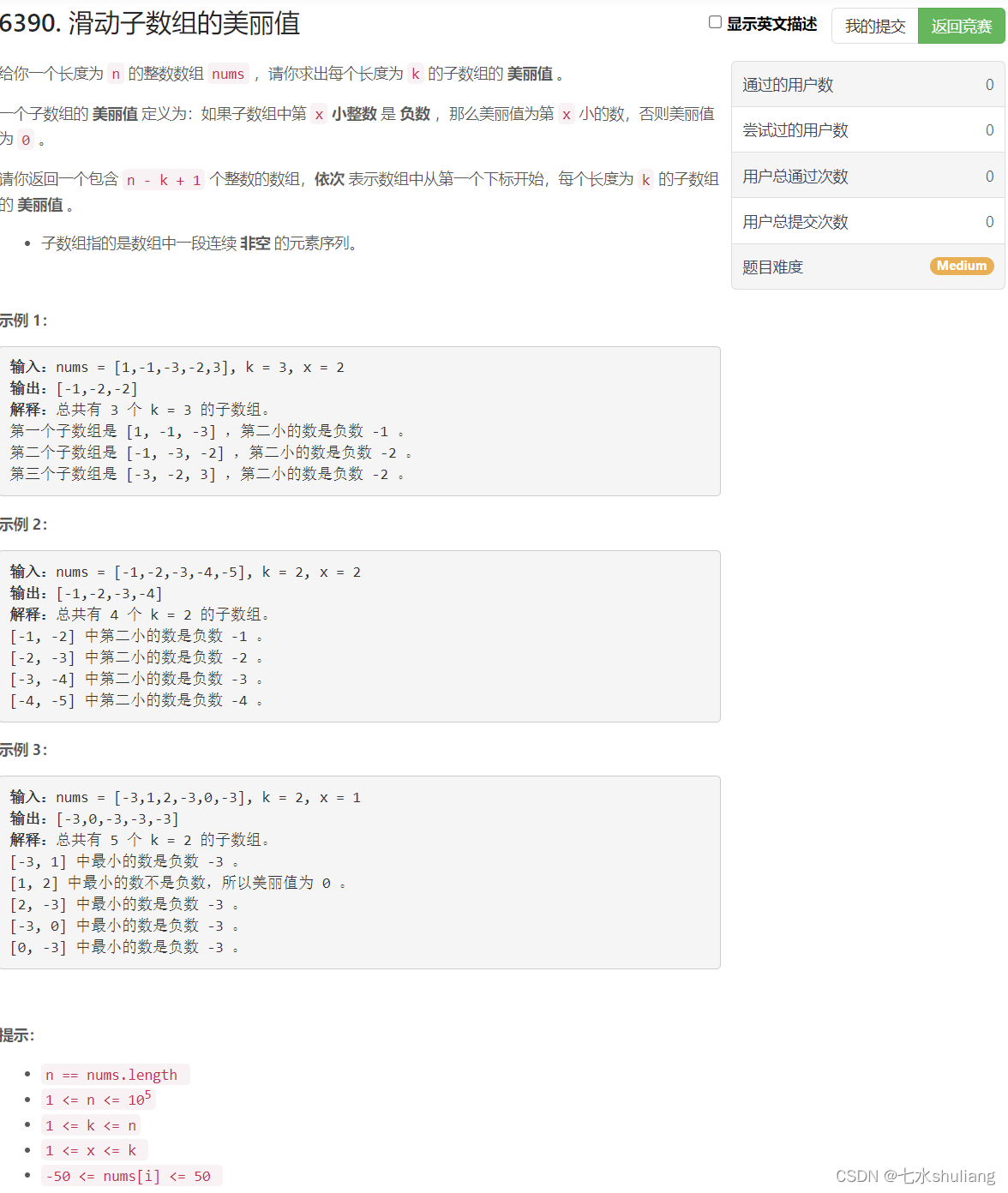
2. 思路分析

• 直接拿名次树滑窗即可。。

---

• 没有名次树可以直接开101数组，桶排序暴力计数。

3. 代码实现

class Solution:
    def getSubarrayBeauty(self, nums: List[int], k: int, x: int) -> List[int]:
        n = len(nums)
        from sortedcontainers import SortedList
        q = deque()
        s = SortedList()
        ans = []
        for r,v in enumerate(nums):
            q.append(v)
            s.add(v)
            if len(q)>k:
                s.remove(q.popleft())
            if len(q) == k:
                p = s[x-1]
                ans.append(min(p,0))
        return ans 

五、 6392. 使数组所有元素变成 1 的最少操作次数

链接: 6392. 使数组所有元素变成 1 的最少操作次数

1. 题目描述

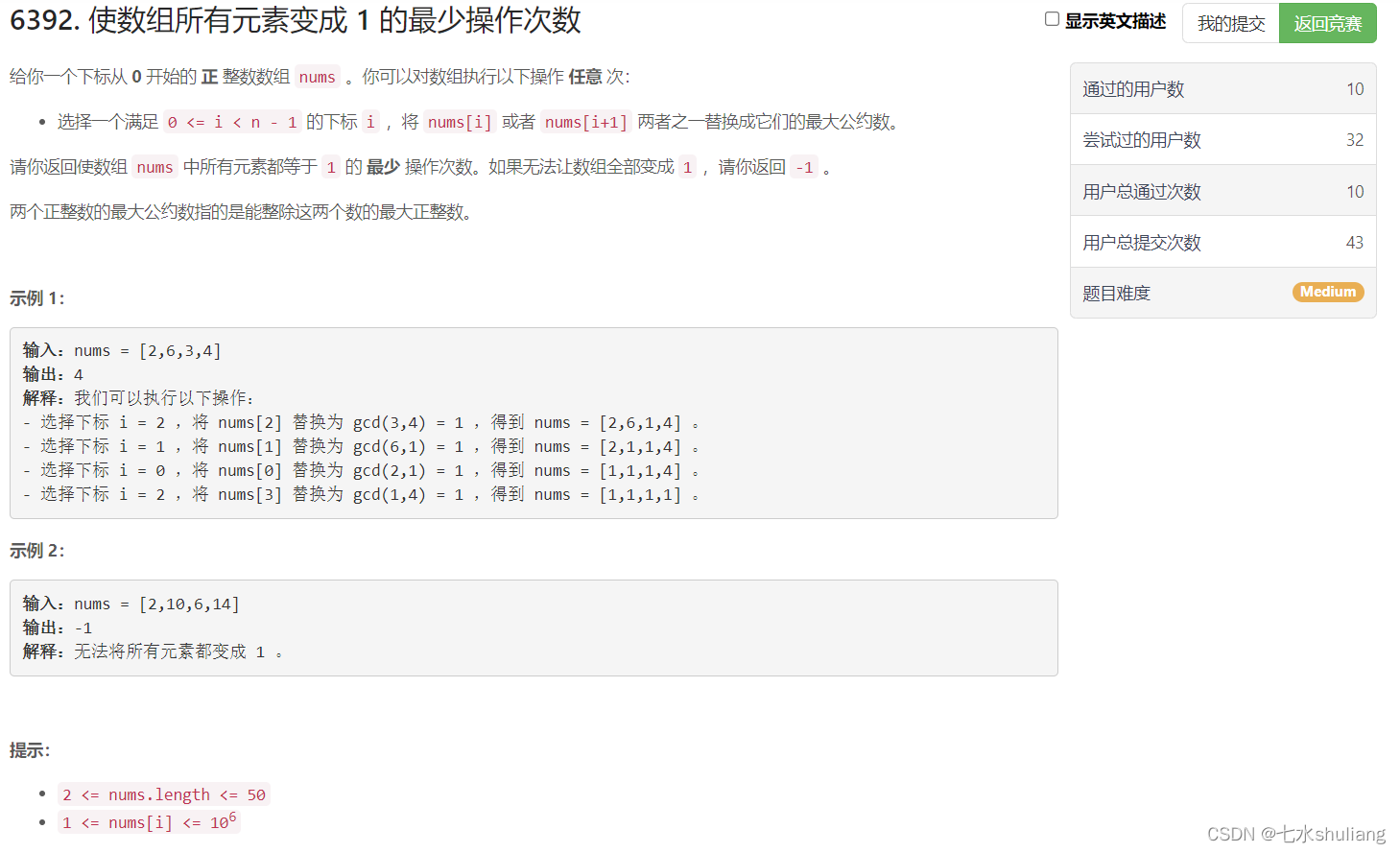
2. 思路分析

蓝桥杯原题n<=1e5。需要st+二分。

• 分析题意可以先贪一下，最优方案是先用最小的代价拼一个1出来，然后用这个1感染其余位置。
• 最小代价一定是相邻的几个数gcd到一起变成1。如果这个长度是d，那么需要操作d-1次变1，最后操作n-1次。答案就是d+n-2。
• 由于数据量小，直接暴力gcd即可，复杂度n方（忽略gcd）
• 如果数据量大，预处理st表，可以计算每段的gcd，由于以某个端点向右的gcd一定是递减的，因此可以二分。枚举左端点，找到最小的为1的段即可。

---

• 暴力写法就不放了，直接放st.

3. 代码实现

class SparseTable:
    def __init__(self, data: list, func=or_):
        # 稀疏表，O(nlgn)预处理，O(1)查询区间最值/或和/gcd
        # 下标从0开始
        self.func = func
        self.st = st = [list(data)]
        i, N = 1, len(st[0])
        while 2 * i <= N+1:
            pre = st[-1]
            st.append([func(pre[j], pre[j + i]) for j in range(N - 2 * i + 1)])
            i <<= 1

    def query(self, begin: int, end: int):  # 查询闭区间[begin, end]的最大值
        lg = (end - begin+1).bit_length() - 1
        # print(lg)
        return self.func(self.st[lg][begin], self.st[lg][end - (1 << lg) + 1])

class Solution:
    def minOperations(self, a: List[int]) -> int:
        n = len(a)
        if gcd(*a) != 1:
            return -1
        c = a.count(1)
        if c:
            return (n-c)
        st = SparseTable(a, gcd)
        ans = inf
        for i in range(n):
            def query(k):
                return st.query(k, i)

            pos = bisect_right(range(i), 1, lo=0, key=query)
            # print(pos,i)
            if pos and query(pos-1) == 1:
                ans = min(ans, i-pos+1)

        return (ans + n - 1)        

六、参考链接