62.不同路径

• 题目链接：代码随想录

• 解题思路：
  1.dp(i)(j)：表示从（0 ，0）出发，到(i, j) 有dp(i)(j)条不同的路径
  2.确定dp的表达式: dp(i)(j) = dp(i-1)(j) + dp(i)(j - 1);到达dp(i)(j)的路径个数为
  到达dp(i - 1)(j)和dp(i)(j - 1)两个方向而来
  3.初始化数组(即确定常量) 观察而至dp(0)(j)= 0 和 dp(i)(0) = 0
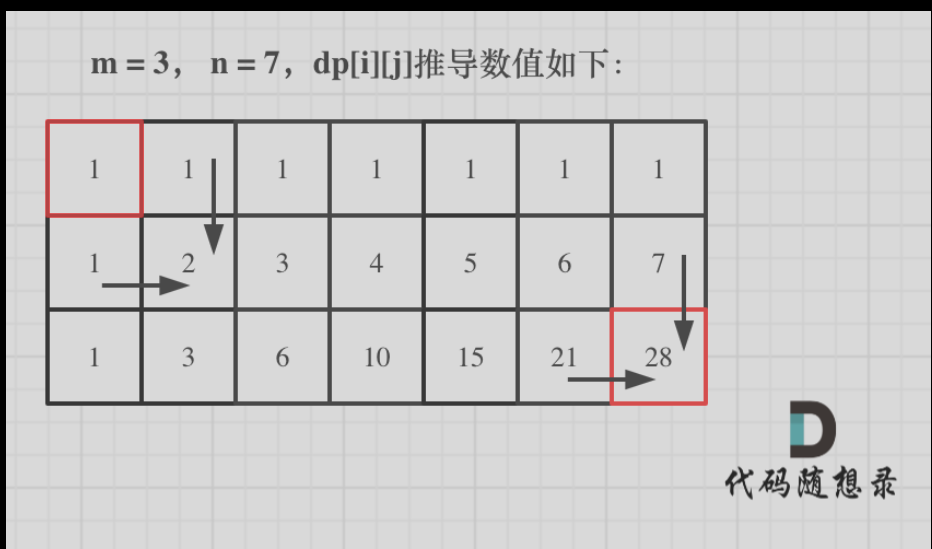
  4.递推公式dp(i)(j) = dp(i-1)(j) + dp(i)(j - 1)都是从其上方和左方推导而来，那么从左到右一层一层遍历就可以了

• 推导过程

  

public int uniquePaths(int m, int n) {
    int[][] dp = new int[m][n];

    for (int i = 0; i < m; i++) {
        dp[i][0] = 1;
    }

    for (int i = 0; i < n; i++) {
        dp[0][i] = 1;
    }

    for (int i = 1; i < m; i++) {
        for (int j = 1; j < n; j++) {
            dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
        }
    }

    return dp[m - 1][n - 1];//注意这里返回值为dp[m - 1][n - 1]
}

63. 不同路径 II

此题与上一题不同是设置了障碍，设置了障碍可以看成障碍处永远到达不了

• 题目链接：代码随想录

• 解题思路：
  1.dp(i)(j) ：表示从（0 ，0）出发，到(i, j) 有dp(i)(j)条不同的路径。
  2.dp(i)(j) = dp(i - 1)(j) + dp(i)(j - 1) 。
  但这里需要注意一点，因为有了障碍，(i, j)如果就是障碍的话应该就保持初始状态（初始状态为0）
  3.dp数组如何初始化
  代码里for循环的终止条件，一旦遇到obstacleGrid(i)(0) == 1的情况就停止dp[i][0]的赋值1的操作
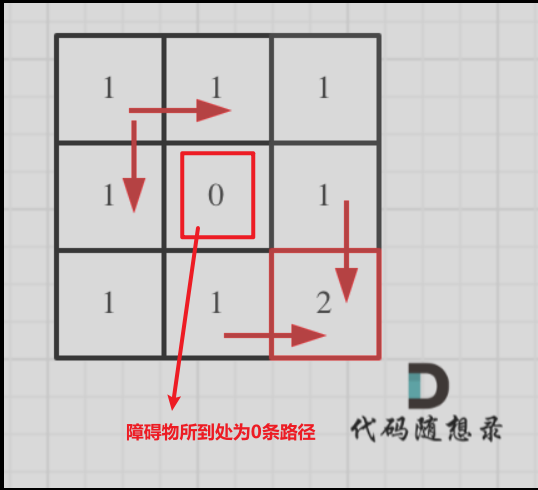
  4.从左到右一层一层遍历，这样保证推导dp(i)(j)的时候，dp(i - 1)(j) 和 dp(i)(j - 1)一定是有数值

• 推导过程

  

public int uniquePathsWithObstacles(int[][] obstacleGrid) {
    //1.m行n列
    int m = obstacleGrid.length;
    int n = obstacleGrid[0].length;

    //2.判断特殊情况
    if(obstacleGrid[0][0] == 1 || obstacleGrid[m - 1][n - 1] == 1){
        return 0;
    }


    int[][] dp = new int[m][n];
    //初始化
    for (int i = 0; i < m; i++) {
        if(obstacleGrid[i][0] == 1){
            break;
        }
        dp[i][0] = 1;
    }

    for (int i = 0; i < n; i++) {
        if(obstacleGrid[0][i] == 1){
            break;
        }
        dp[0][i] = 1;
    }

    for (int i = 1; i < m; i++) {
        for (int j = 1; j < n; j++) {

            if(obstacleGrid[i][j] == 1){
                dp[i][j] = 0;
                continue;
            }

            dp[i][j] = dp[i - 1][j] + dp[i][j - 1];

        }
    }

    return dp[m - 1][n - 1];
}