目录
- 简单的暴力匹配算法
- KMP算法
- next数组
- next数组的优化
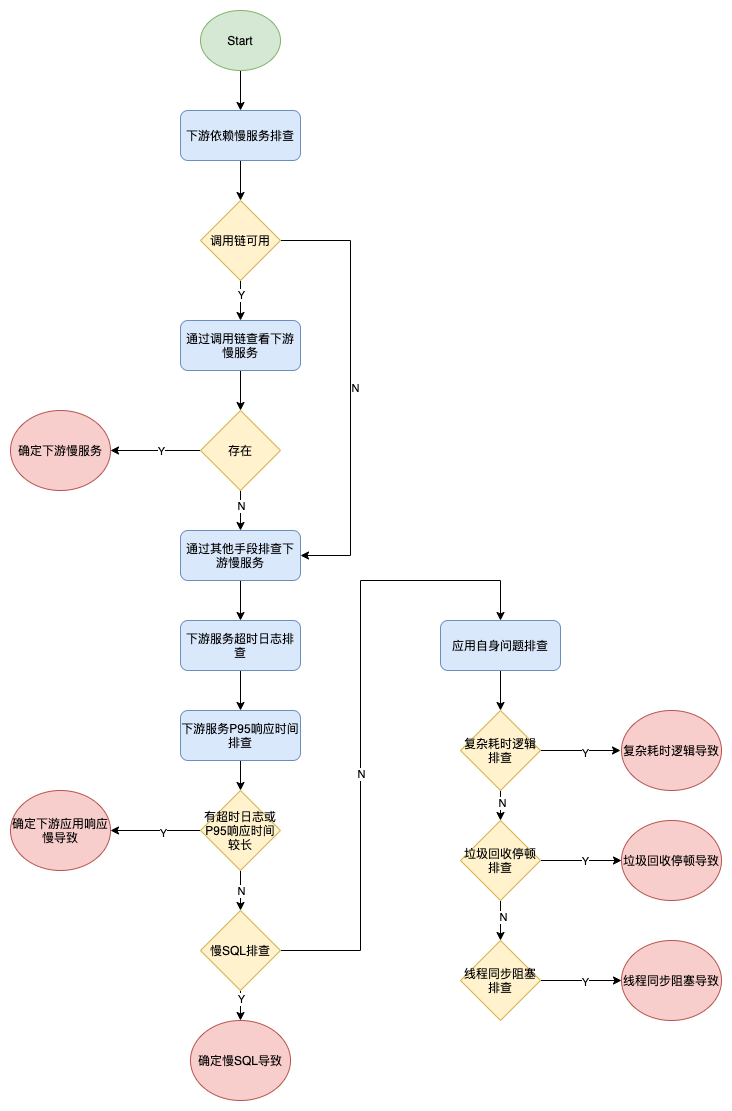
简单的暴力匹配算法
对于字符串的匹配通常是给出一个主串str和一个模式串sub,然后在主串pos位置开始匹配,如果能在str中找到sub那么就返回sub在str中首次出现的首个字符的下标,否则返回-1。我们能想到的最直接的方法就是用三个指针p,i,j 这里我们就以pos=0 为例子讲解,先让p=0,i=p,j=0,开始匹配
如果str[i]==sub[j] 那么++i,++j 如果不相等那么j回到初始位置即j=0,然后p++ ,i=p,也就是i又从上一轮往后一个位置开始匹配,最后如果j能走到末尾就匹配成功返回 i-j; 否则返回-1,这种暴力算法时间复杂度是O(n^2)。
int strStr(string str, string sub,int pos) {
int i=pos;
int j=0;
int m=str.size(),n=sub.size();
if(m==0||n==0) return -1;
while(i<m&&j<n)
{
if(str[i]==sub[j])
{
++i;
++j;
}
else
{
++pos;
i=pos;
j=0;
}
}
if(j>=n)
return i-j;
return -1;
}
KMP算法
KMP算法是一种改进的字符串匹配算法,其核心就是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next函数实现,函数本身包含了模式串的局部匹配信息,KMP算法的时间复杂度O(m+n)。
KMP和BF唯一不一样的地方在,主串的i不管匹配成功与否都不会回退,j也不一定每次都回退到0位置,j该回退的位置我们都记录在next数组中。

比如上图,i和j从0位置开始匹配,在5位置匹配失败,这是j可以只要回退到2位置继续和i匹配
可以知道,i能走到5位置自然是前面有一部分匹配上了,这里 str 3 4 位置就跟sub 0 1位置匹配上l
所以i不回退,j从2位置继续匹配。我们把每次匹配失败对于该回退到那个位置记录在next[j]中
next数组
KMP的精髓就是next数组用next[j]=K 来表示,sub在j位置匹配失败,应该回退到k位置取,求next数组的规则是
1.找到匹配成功部分的两个相等的真子串,不能是同一个,一个以下标0字符开始,另一个以j-1下标字符结尾。
2.就是初始化next数组,不管什么数据next[0]=-1,next[1]=0,
next[j]=k就是说找到了两个相等的真子串 sub[0]…sub[k-1] 和sub[x]…sub[j-1] 长度就是k,找不到就是0
比如求”ababcabcdabcde”的next数组

求对”abcabcabcabcdabcde”
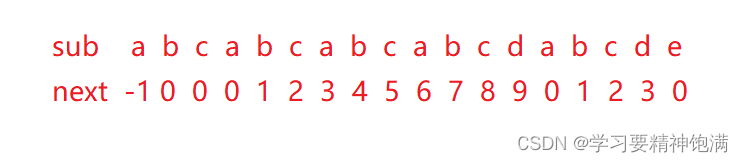
所以通过目测可以算出next[j],接下来就要思考,如果已经知道了next[i]的值,如果求next[i+1]的值
通过上面连个例子可以看出,相邻位置的k值增加大方式只能是+1,不会跳跃式增加,实际上,减少的方式不一定是直接到0,如果next[i]=k 那就是sub[0]…sub[k-1] 和sub[x]…sub[i-1]相等,现在要计算next[i+1] 应该判断sub[k]==next[i] 是否为真,如果为真就有sub[0]…sub[k-1] sub[k] 和
sub[x]…sub[i-1] sub[i] 是连个相等的真字串了,长度就是k+1 也就是next[i+1]=k+1,如果不相等k
就要回退到next[k] 即 k=next[k] 所以我们就可以通过sub 计算出next数组了
void getnext(const string&sub,vector<int>&next)
{
int n=next.size();
next[0]=-1;
if(n>1) // 防止越界 ,后面有 i<n判断不会越界
next[1]=0;
int k=0; //完成了 0 1 位置的初始化,就开始计算下面next位置的值了,这里k就是1位置的值
int i=2;
while(i<n)
{
if(k==-1||sub[i-1]==needle[k]) //如果回退到了-1 那么i位置就应该退到0 所以也进入然后设置为0
{
next[i]=k+1;
++k; //设置完i位置 后面i+1,的值我们要用i位置的k值 所以也是k++
++i;
}
else
{
k=next[k]; //回退
}
}
}
int KMP(const string&str,const string&sub,int pos)
{
int i=pos;
int j=0;
int m=str.size();
int n=sub.size();
if(m==0||n==0) return -1; //前期的判断
vector<int>next(n),nextval(n);
getnext(sub, next); // 有优化后的next数组,即nextval数组,用其中任意一个都行
getnextval(sub, next,nextval);
while(i<m&&j<n)
{
if(j==-1||str[i]==sub[j]) //同样如果j在初始时就匹配失败了,跳到-1了同样可以进入让i++ ,j从0开始匹配
{
++i;
++j;
}
else
{
// j=next[j];
j=nextval[j];
}
}
if(j>=n)
return i-j;
return -1;
}
next数组的优化
我们在一个位置匹配失败j是回退的,因为str[i]!=sub[j] 回退有j=next[j] 如果回退位置的字符和没回退位置的字符时相同的那么还是会匹配失败,继续回退,所有我们优化,然后回退一步到位
比如 sub aaaaaaaab

nextval数组的求法就是,首先nextval[0]自然是-1 后面i>0, 如果当前要回退到的位置的字符正好等于当前字符,那么i处的nextval值就是回退位置的nextval值,否则就是自己的next值
void getnextval(const string&sub,const vector<int>&next,vector<int>&nextval)
{
nextval[0]=-1;
int n=nextval.size();
for(int i=1;i<n;++i)
{
if(sub[i]==sub[next[i]])
nextval[i]=nextval[next[i]];
else
nextval[i]=next[i];
}
}