目录
一、前言
二、BF 算法
三、KMP 算法
3.2.1 - KMP 算法的原理
3.2.2 - KMP 算法的实现
3.2.3 - KMP 算法的优化
创作不易,可以点点赞,如果能关注一下博主就更好了~
一、前言
子串的定位运算通常称为串的模式匹配或串匹配。此运算的应用非常广泛,比如在搜索引擎、拼写检查、语言翻译、数据压缩等应用中,都需要进行串匹配。
串的模式匹配设有两个字符串 S 和 T,设 S 为主串,也称正文串;设 T 为子串,也称为模式。在主串 S 中查找与模式 T 相匹配的子串,如果匹配成功,确定相匹配的子串中的第一个字符在主串 S 中出现的位置。
著名的模式匹配算法有 BF 算法和 KMP 算法。
二、BF 算法
BF 算法,即暴力(Brute Force)算法,是最简单直观的模式匹配算法。
int IndexBF(const char* S, const char* T)
{
if (S == NULL || T == NULL) // 判断是否为空指针
return -1;
int i = 0; // 主串指针
int j = 0; // 模式串指针
int slen = strlen(S);
int tlen = strlen(T);
while (i < slen && j < tlen)
{
if (S[i] == T[j])
{
++i;
++j;
}
else
{
// 回溯
i = i - j + 1; // i = i - (j - 1) = i - j + 1
j = 0;
}
}
if (j == tlen)
return i - j; // 匹配成功
else
return -1; // 匹配失败
}
三、KMP 算法
3.2.1 - KMP 算法的原理
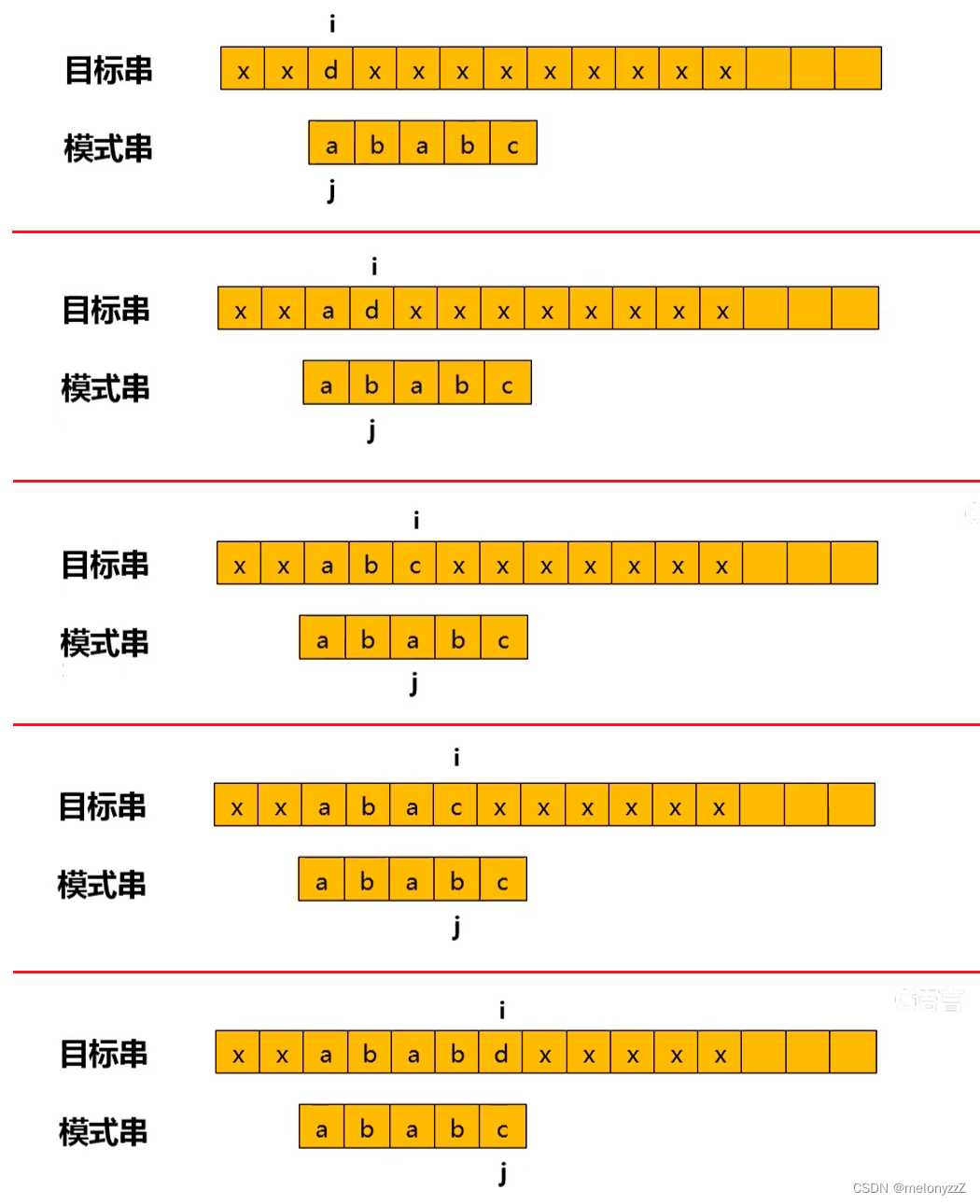
KMP 是对 BF 改进后的算法,它由 Knuth、Morris 和 Pratt 同时设计实现,因此简称 KMP 算法。
在 BF 算法中,每当一趟匹配过程中出现字符不相等的情况,主串指针 i 回溯到下标为 i - j + 1 的位置,这是因为在模式匹配中,我们并不知道主串的具体内容,但是在不匹配的字符之前,主串 S 中的一个连续的字符序列与模式串相等,KMP 算法正是利用了已经得到的 "部分匹配" 结果对算法进行了改进。
KMP 算法的原理:
-
在匹配的过程中,主串的指针
i不需要回溯,只回溯模式串的指针j。 -
当
S[i] != T[j]时,模式串指针j回溯的下标位置由模式串的内容决定。
假设主串为
,模式串为
,在匹配过程中,当
时,模式串指针
j回溯到下标为k (k < j)的位置,则有①。
而已得到的 "部分匹配" 的结果是
②。
由 ① 和 ② 推得
③,它们是模式串匹配失败位置前的内容中的最长公共前后缀。
例如:
j
前缀 后缀 最长公共前后缀 k 0 无 无 无 无 -1 1 a 无 无 无 0 2 ab a b 无 0 3 aba a、ab a、ba a 1 4 abab a、ab、aba b、ab、bab ab 2 令
next[j] = k,则next[j]表示在匹配过程中,当 时,模式串指针
j回溯的下标位置。
3.2.2 - KMP 算法的实现
void GetNext(const char* T, int* next)
{
int tlen = strlen(T);
if (tlen == 0) { return; }
if (tlen == 1) { next[0] = -1; return; }
if (tlen == 2) { next[0] = -1; next[1] = 0; return; }
// 计算 next[j]
next[0] = -1;
next[1] = 0;
for (int j = 2; j < tlen; ++j)
{
int maxlen = 0; // 最长公共前后缀的长度
for (int i = 1; i < j; ++i)
{
char* prefix = (char*)calloc(i + 1, sizeof(char));
char* suffix = (char*)calloc(i + 1, sizeof(char));
assert(prefix && suffix);
strncpy(prefix, T, i); // 取前缀
strncpy(suffix, T + j - i, i); // 取后缀
// 判断是否为公共前后缀
if (strcmp(prefix, suffix) == 0)
{
maxlen = i;
}
}
next[j] = maxlen;
}
}
int IndexKMP(const char* S, const char* T)
{
if (S == NULL || T == NULL) // 判断是否为空指针
return -1;
int i = 0; // 主串指针
int j = 0; // 模式串指针
int slen = strlen(S);
int tlen = strlen(T);
// 获取 next 数组
int* next = (int*)calloc(tlen, sizeof(int));
assert(next);
GetNext(T, next);
while (i < slen && j < tlen)
{
if (S[i] == T[j] || j == -1)
{
++i;
++j;
}
else
{
j = next[j]; // 根据 next 数组回溯模式串指针
}
}
if (j == tlen)
return i - j; // 匹配成功
else
return -1; // 匹配失败
return 0;
}
3.2.3 - KMP 算法的优化
前面定义的 next 数组在某些情况下尚有缺陷。例如模式串 和主串 匹配时,当 S[3] != T[4] 时,由 next[j] 的指示还需要进行 i = 3、j = 2; i = 3、j = 1; i = 3、j = 0 这三次比较。实际上,因为模式串中下标分别为 2、1、0 的三个字符和下标为 3 的字符相等,因此不需要再和主串中下标为 3 的字符相比较,而可以直接进行 i = 4、j = 0 的字符比较。
这就是说,若按上述定义得到 next[j] = k,而模式串中 ,则当 时,不需要再和 进行比较,而直接和 比较,换句话说,此时的 next[j] 应该和 next[k] 相同。
void GetNext(const char* T, int* next)
{
int tlen = strlen(T);
if (tlen == 0) { return; }
if (tlen == 1) { next[0] = -1; return; }
if (tlen == 2) { next[0] = -1; next[1] = 0; return; }
// 计算 next[j]
next[0] = -1;
next[1] = 0;
for (int j = 2; j < tlen; ++j)
{
int maxlen = 0; // 最长公共前后缀的长度
for (int i = 1; i < j; ++i)
{
char* prefix = (char*)calloc(i + 1, sizeof(char));
char* suffix = (char*)calloc(i + 1, sizeof(char));
assert(prefix && suffix);
strncpy(prefix, T, i); // 取前缀
strncpy(suffix, T + j - i, i); // 取后缀
// 判断是否为公共前后缀
if (strcmp(prefix, suffix) == 0)
{
maxlen = i;
}
}
next[j] = maxlen;
}
}
void GetNextval(const char* T, int* next, int* nextval)
{
int tlen = strlen(T);
nextval[0] = -1;
for (int j = 1; j < tlen; ++j)
{
if (T[j] == T[next[j]])
{
nextval[j] = nextval[next[j]];
}
else
{
nextval[j] = next[j];
}
}
}
int IndexKMP(const char* S, const char* T)
{
if (S == NULL || T == NULL) // 判断是否为空指针
return -1;
int i = 0; // 主串指针
int j = 0; // 模式串指针
int slen = strlen(S);
int tlen = strlen(T);
// 获取 next 数组
int* next = (int*)calloc(tlen, sizeof(int));
assert(next);
GetNext(T, next);
// 获取 nextval 数组
int* nextval = (int*)calloc(tlen, sizeof(int));
assert(nextval);
GetNextval(T, next, nextval);
while (i < slen && j < tlen)
{
if (S[i] == T[j] || j == -1)
{
++i;
++j;
}
else
{
j = nextval[j]; // 根据 nextval 数组回溯模式串指针
}
}
if (j == tlen)
return i - j; // 匹配成功
else
return -1; // 匹配失败
return 0;
}