基于用户的协同过滤算法userCF
1.1 相似度计算
通过计算用户之间的相似度。这里的相似度指的是两个用户的兴趣相似度。
假设对于用户u uu和v vv,N ( u ) N(u)N(u)指的是用户u uu喜欢的物品集合,N ( v ) N(v)N(v)指的是用户v vv喜欢的物品集合,可以通过Jaccard公式计算u uu和v vv的相似度:
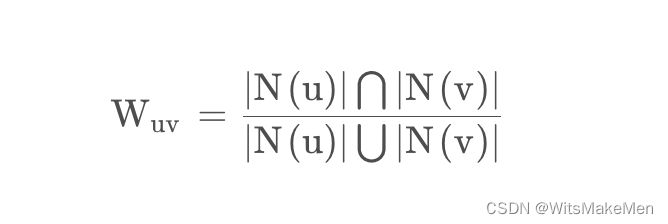
或者通过余弦相似度来计算:

这种方法需要计算两两用户之间的相似度,复杂度为O ( ∣ U ∣ 2 ) O(|U|^2)O(∣U∣
2
),这种方法非常耗时,特别是大量的用户之间没有相关性时,即∣ N ( u ) ∣ ⋂ ∣ N ( v ) ∣ |N(u)|\bigcap|N(v)|∣N(u)∣⋂∣N(v)∣为0,对这些用户的计算是完全不需要的。因此,只需先判断∣ N ( u ) ∣ ⋂ ∣ N ( v ) ∣ |N(u)|\bigcap|N(v)|∣N(u)∣⋂∣N(v)∣是否为0,为0的用户之间计算相似度即可。

对于矩阵1.1,首先建立从物品到用户的二维倒排表,每一个物品都在表中占据一行。对于表的每一行,首个元素是一个物品,如果某用户u对该物品产生过行为,则将u加入到该行中。对于每一行的用户列表,里面的用户两两之间都存在着相似性。

然后,建立|U| X |U|的稀疏矩阵C,首先,初始化C的各个元素为0,
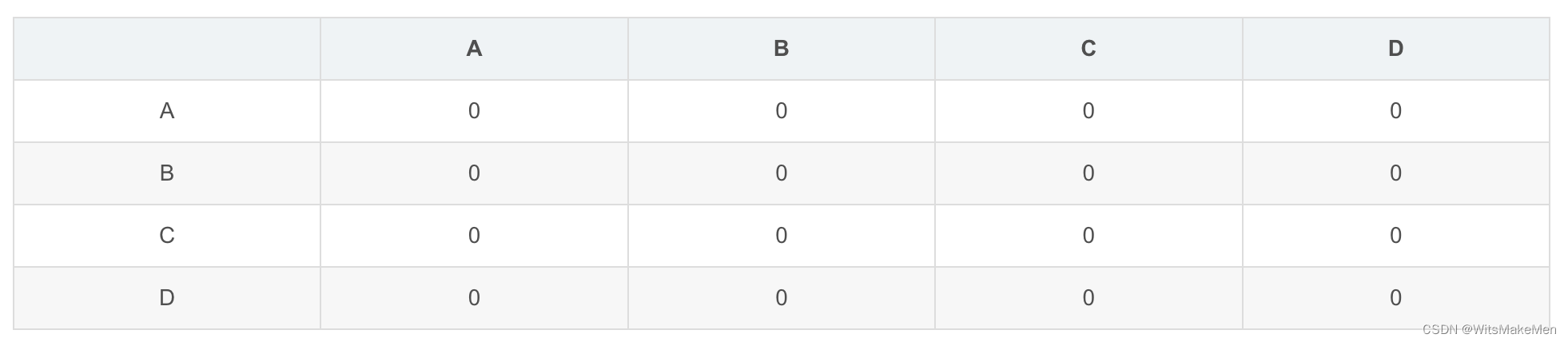
如果用户u和用户v同时在倒排表的k行中出现过,那么说明u和v共同对这k个物品产生过行为,遍历二维倒排表的每一行中的用户列表,对于其中的任意两个用户u和v,将C[u][v]和C[v][u]加1。这样,遍历完成之后,C[u][v]的值就等于:
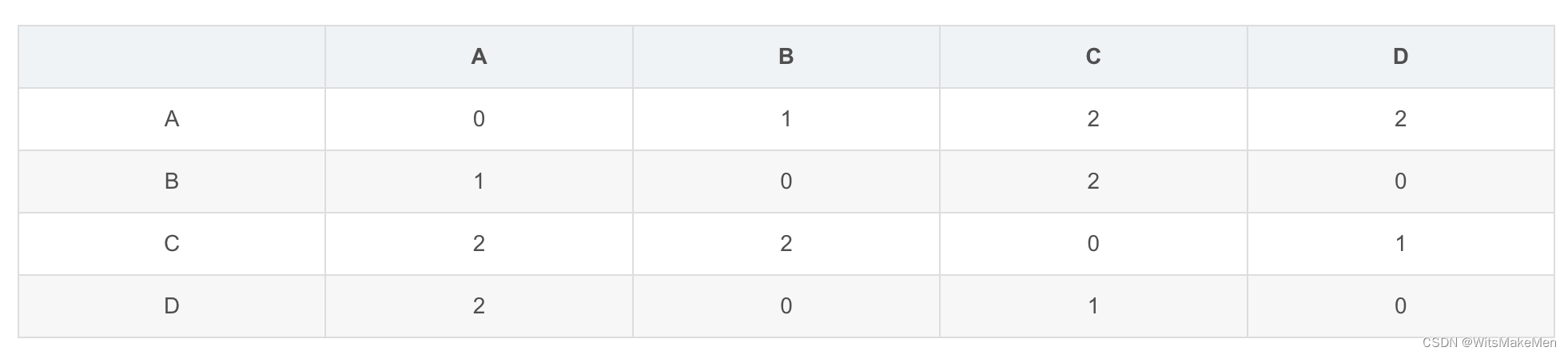
可知,上述矩阵是一个对称矩阵。
1.2 topN推荐
在计算出了所有用户两两之间的相似度后,userCF算法会向用户推荐与它兴趣相近的k个用户最喜欢的物品,如下公式度量了用户u对物品i的感兴趣程度:
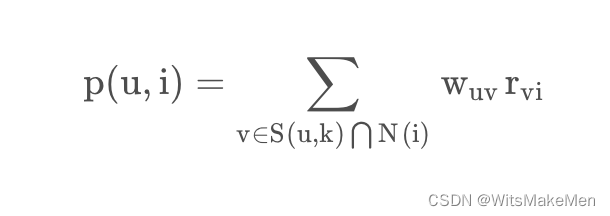

1.3 算法参数
参数k是UserCF算法的重要参数,它对推荐算法的各种指标都会产生一些列的影响:
精度(准确率和召回率):准确率和召回率与参数k并不呈线性关系,但是选择合适的k对于获得推荐系统高的精度比较重要。
流行度:k越大,则UserCF推荐的物品就越热门。
覆盖率:k越大,流行度就越大,而覆盖率会相应地越小。
参考链接:
https://www.zybuluo.com/xtccc/note/200979
仅为笔记记录使用,侵删。