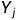Faster RCNN系列3——RPN的真值详解与损失值计算

news2024/9/20 6:37:49

Faster RCNN系列：

Faster RCNN系列1——Anchor生成过程
Faster RCNN系列2——RPN的真值与预测值概述
Faster RCNN系列3——RPN的真值详解与损失值计算
Faster RCNN系列4——生成Proposal与RoI
Faster RCNN系列5——RoI Pooling与全连接层

一、RPN真值详解

RPN的真值分为类别真值和偏移量真值，即每一个Anchor是否对应着真实物体，以及每一个Anchor对应物体的真实偏移值，这两种真值的具体求解过程如下图所示：

在这里插入图片描述

Anchor生成

Anchor生成的具体过程可参考Faster RCNN系列——Anchor生成过程，可生成 $37 \times 50 \times 9 = 16650$ 个Anchors，这种方法对于靠近图像边缘的点来说，可能生成超出图像范围的Anchor，需要把这部分超过图像范围的Anchor过滤掉。

def forward(self, input):
	# 利用NumPy首先得到原图上的中心点坐标，并利用contiguous保证内存连续
	shifts = torch. from_numpy(np.vstack((shift_x.ravel(), shift__y.ravel(),
										  shift_x.rave1(), shift_y.rave1())).transpose())
	shifts = shifts.contiguous().type_as(rpn_cls_score) .float ()
	# 调用基础Anchor生成所有Anchors
	self.anchors = self.anchors.type_as(gt_boxes)
	all_ anchors = self. anchors.view(1, A, 4) + shifts.view(K, 1, 4)
	# 保留边框内的Anchors
	inds_inside = torch.nonzero(keep).view(-1)
	anchors = all_ anchors[inds_inside, :]

类别真值求解

类别真值求解的详细过程可参考Faster RCNN系列——RPN的真值与预测值概述中类别真值的部分，需要注意的是，求解过程中的三个步骤的顺序不能变动，原因：

保证一个Anchor既符合正样本，也符合负样本时，才会被赋予正样本。
为了保证召回率，允许一个标签对应多个Anchor，不允许一个Anchor对应多个标签。

def forward(self, input):
	# 生成标签向量，对应每一个Anchor的状态，1为正，0为负，初始化为-1
	labels = gt_boxes.new(batch_size, inds_inside.size(0)).fill_(-1)
	# 生成IoU矩阵，每一行代表一个Anchor, 每一列代表一个标签
	overlaps = bbox_overlaps_batch(anchors, gt_boxes)
	# 对每一行求最大值，返回的第一个为最大值，第二个为最大值的位置
	max_overlaps, argmax_overlaps = torch.max(overlaps, 2)
	# 对每一列取最大值，返回的是每一个标签对应的IoU最大值
	gt_max_overlaps, _ = torch.max(overlaps, 1)
	# 如果一个Anchor最大的IoU小于0.3, 视为负样本
	labels[max_overlaps < 0.3] = 0
	#与所有Anchors的最大IoU为0的标签要过滤掉
	gt_ max_overlaps[gt_max_overlaps==0] = 1e-5
	# 将与标签有最大IoU的Anchor赋予正样本
	keep = torch.sum(overlaps.eq(gt_max_overlaps.view(batch_size, 1, -1).expand_as(overlaps)), 2)
	if torch.sum(keep)>0:
		labels[keep>0] = 1
	#  如果一个 Anchor最大的IoU大于0.7,视为正样本
	labels[max_overlaps >= 0.7] = 1

Anchor的筛选

由于Anchor的总数量接近于2万，并且大部分Anchor的标签都是背景，如果都计算损失的话则正、负样本失去了均衡，不利于网络的收敛。因此，RPN默认选择256个Anchors进行损失的计算，其中最多不超过128个的正样本。如果数量超过了限定值，则进行随机选取。当然，这里的256与128都可以根据实际情况进行调整，而不是固定死的。

def forward(self, input):
	......
	for i in range(batch_size):
	#如果正样本数量太多，则进行下采样随机选取
		if sum_fg[i] > 128 :
			fg_inds = torch.nonzero(labels[i] == 1).view(-1)
			rand_num = torch.from_numpy(np.random.permutation
			(fg_ inds.size(0))).type_as(gt_boxes).long()
			disable_inds = fg_inds[rand_num[:fg_inds.size(0)-num_fg]]
			labels[i][disable_inds] = -1
			# 负样本同上
			......

偏移量真值求解

偏移量真值的求解过程可参考Faster RCNN系列——RPN的真值与预测值概述中偏移量真值的部分。

得到偏移量的真值后，将其保存在bbox_ targets 中。与此同时，还需要求解两个权值矩阵bbox_inside_weights 和bbox_outside_weights，前者是用来设置正样本回归的权重，正样本设置为1，负样本设置为0，因为负样本对应的是背景，不需要进行回归；后者的作用则是平衡RPN分类损失与回归损失的权重，在此设置为1/256。

def forward(self, input):
	......
	# 选择每一个Anchor对应最大Iou的标签进行偏移计算
	bbox_targets = _compute_targets_batch(anchors, gt_ boxes.view(-1, 5)[argmax_overlaps.view(-1), :].view(batch_size, -1, 5))
	#设置两个权重向量
	bbox_inside_weights[labels==1] = 1
	num_examples = torch.sum(labels[i] >=0)
	bbox_outside_weights[labels == 1] = 1.0 / examples.item()
	bbox_outside_weights[labels == 0]=1.0 / examples.item()

二、RPN预测值

RPN的预测值分为类别预测值和偏移量预测值，计算过程可参考Faster RCNN系列——RPN的真值与预测值概述，通过卷积神经网络的分类分支求得类别预测值、通过回归分支求得偏移量预测值。

三、损失值计算

有了类别真值、偏移量真值、类别预测值、偏移量预测值，就可以计算RPN网络的损失函数了。RPN网络的损失函数包含类别损失和回归损失，公式如下：

$L(P_{i},t_{i})=\frac{1}{N_{cls}}\sum L_{cls}(p_{i},p_{i}^{*})+\lambda \frac{1}{N_{reg}}\sum p_{i}^{*}L_{reg}(t_{i},t_{i}^{*})$

$\sum L_{cls}(p_{i},p_{i}^{*})$ 表示筛选出的256个Anchor的类别损失， $p_{i}$ 为每一个Anchor的类别真值， $p_{i}^{*}$ 为每一个Anchor的类别预测值。这里的类别只有前景和背景之分，为二分类，因此类别损失函数 $L_{cls}$ 使用交叉熵损失函数，公式如下：

$L_{cls}(p_{i},p_{i}^{*})=-\sum p_{i}logp_{i}^{*}$

$\sum p_{i}^{*}L_{reg}(t_{i},t_{i}^{*})$ 表示回归损失， $t_{i}$ 为每一个Anchor的偏移量真值， $t_{i}^{*}$ 为每一个Anchor的偏移量预测值。这里的 $p_{i}^{*}$ 对应上文中的bbox_inside_weights，用来筛选正负样本，这里的 $\lambda \frac{1}{N_{reg}}$ 对应上文中的bbox_outside_weights，用来平衡类别损失和回归损失。回归损失函数 $L_{reg}$ 使用 $smooth_{L1}$ 函数，公式如下：