C++语法（20）---- 模拟红黑树

news2024/9/20 8:11:28

C++语法（19）---- 模拟AVL树_哈里沃克的博客-CSDN博客https://blog.csdn.net/m0_63488627/article/details/130229501?spm=1001.2014.3001.5501

目录

1.红黑树介绍

2.模拟实现

1.枚举红黑颜色

2.节点的定义

3.树类框架

4.插入

5.检查

3.代码实现

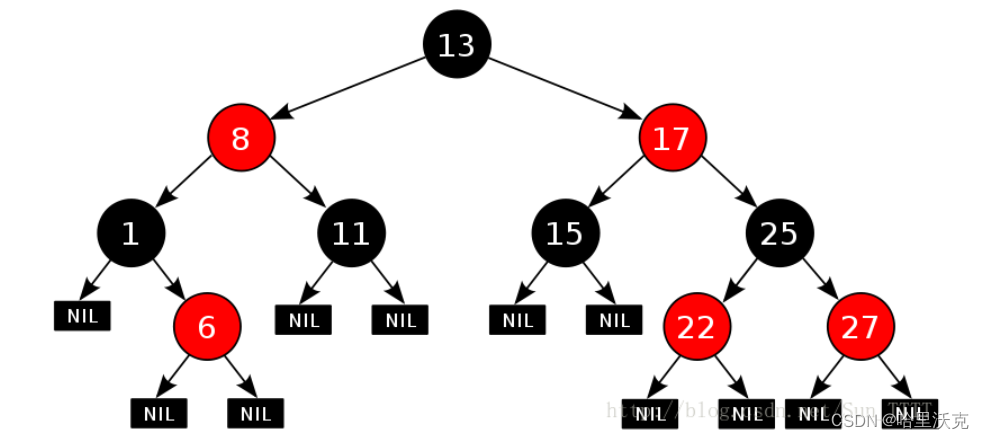
1.红黑树介绍

最长路径不超过最短路径的两倍，近似平衡

最短：全黑

最长：一半黑一半红

1.每个节点不是红色就是黑色

2.根节点是黑色

3.如果一个节点是红色，它的两个孩子节点是黑色

4.每条路径都有相同数量的黑色节点

5.叶子节点(NIL节点)是黑的

满二叉树：全黑，或者每条路径一黑一红

较优情况：越均衡即越平衡

最差红黑树：左边全黑，右边一黑一红

较差情况：越不均衡

对比起AVL树，其实红黑树没有那么的较劲平衡，AVL的平衡得益于它不断的旋转。但是红黑树为了一些性能牺牲了平衡，减少了旋转的情况。

2.模拟实现

1.枚举红黑颜色

enum Color
{
	Black,
	Red,
};

2.节点的定义

template<class K, class V>
struct BRTreeNode
{
	pair<K, V> _kv;
	BRTreeNode* _left;
	BRTreeNode* _right;
	BRTreeNode* _parent;
	Color _col;

	BRTreeNode(const pair<K, V>& kv)
		:_kv(kv)
		, _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _col(Red)
	{}
};

定义一个节点时要注意其颜色：不过黑红的地位有所不同，选择决定后续的执行是否简单

选择红色：违背红色不能连续出现

选择黑色：违背整体路径黑色数量一致

我们认为选择红色更好，因为红色调节节点即可，黑色调节整个路径

3.树类框架

template<class K, class V>
class BRTree
{
private:
	Node* _root = nullptr;
};

4.插入

1.插入的头节点为根节点，根节点的颜色为黑色

2.普通插入的逻辑和搜索二叉树的逻辑一致

3.到这里就需判断是否两个红色节点连续，下面的问题就是调节双红色问题

调节双红色问题

情况一

 插入红色节点其父节点和叔叔节点都是红色，那么我们要调整父节点和叔叔节点为黑色，不过如果只是调整这一步，那么这条树的分支就比别的树黑色节点多一个，所以我们还要更新祖父节点为红色，但是祖父为红不能保证它的父节点是黑的，所以我们仍然要往上判断

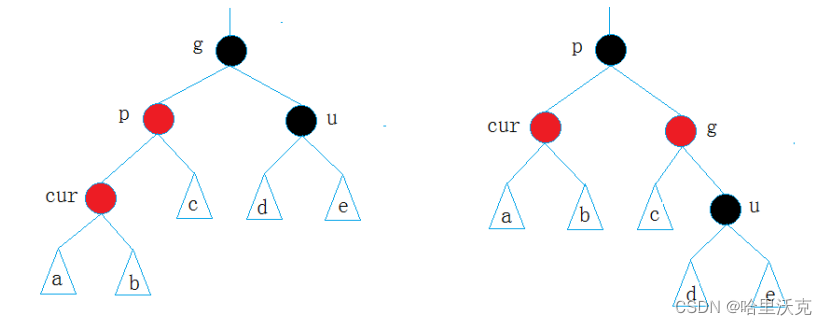
情况二

单旋加变色

叔叔节点是黑色或者不存在，如果只是把父节点变黑是不够的，因为高度超了，所以我们要用到左右旋。 

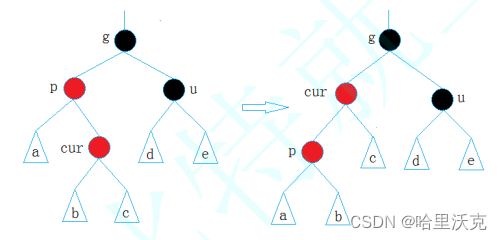
情况三

双旋加变色

这样就变成了情况二 

bool Insert(const pair<K, V>& kv)
{
	if (_root == nullptr)
	{
		_root = new Node(kv);
		_root->_col = Black;
		return true;
	}

	//父子节点确定插入的位置
	Node* parent = nullptr;
	Node* cur = _root;
	while (cur)
	{
		if (cur->_kv.first > kv.first)
		{
			parent = cur;
		    cur = cur->_left;
		}
		else if (cur->_kv.first < kv.first)
		{
			parent = cur;
			cur = cur->_right;
		}
		else
			return false;
	}

	//走到这cur就是要插入的位置
	//cur要连接parent，parent也要连接cur---判断靠kv的大小
	cur = new Node(kv);
	if (parent->_kv.first > cur->_kv.first)
	{
		parent->_left = cur;
		cur->_parent = parent;
	}
	else
	{
		parent->_right = cur;
		cur->_parent = parent;
	}

	while (parent && parent->_col == Red)
	{
		Node* grandparent = parent->_parent;
		//parent分在grandparent左右
		if (grandparent->_left == parent)
		{
			//关键是看uncle节点不存在/红色/黑色的情况
			Node* uncle = grandparent->_right;
			//1.uncle红
			//parent和uncle变黑，grandparent变红
			//grandparent变红需要往上判断
			if (uncle && uncle->_col == Red)
			{
				grandparent->_col = Red;
				parent->_col = uncle->_col = Black;

				cur = grandparent;
				parent = cur->_parent;
			}
            else  //uncle不存在/黑色
			{
				//2.cur也是parent的左边，uncle不存在/黑色
				//右旋grandparents，parent变黑，
				if (cur == parent->_left)
				{
					_RotateR(grandparent);
					parent->_col = Black;
					grandparent->_col = Red;
				}
				//3.cur是parent的右边，uncle不存在/黑色
				//左旋parent再右旋grandparents,cur变黑，grandparents变红
				else
				{
					_RotateL(parent);
					_RotateR(grandparent);
					cur->_col = Black;
					grandparent->_col = Red;
				}

				//抽象树的头被设置为黑色，对上面没有影响，所以不需要进行循环
				break;
			}
				
		}
        else
		{
		Node* uncle = grandparent->_left;

		    //1.uncle红
		    //parent和uncle变黑，grandparent变红
		    //grandparent变红需要往上判断
		    if (uncle && uncle->_col == Red)
		    {
			    grandparent->_col = Red;
			    parent->_col = uncle->_col = Black;

			    cur = grandparent;
			    parent = cur->_parent;
		    }
			else  //uncle不存在/黑色
			{
				//2.cur也是parent的右边，uncle不存在/黑色
				//左旋grandparents，parent变黑，
				if (cur == parent->_right)
				{
					_RotateL(grandparent);
					parent->_col = Black;
					grandparent->_col = Red;
				}
				//3.cur是parent的右边，uncle不存在/黑色
				//右旋parent再左旋grandparents,cur变黑，grandparents变红
				else
				{
					_RotateR(parent);
					_RotateL(grandparent);
					cur->_col = Black;
					grandparent->_col = Red;
				}

				//抽象树的头被设置为黑色，对上面没有影响，所以不需要进行循环
				break;
			}
		}
	}
	_root->_col = Black;
	return true;
}

5.检查

inspect函数

1.空树返回true

2.根节点是否是红的

3.先遍历最左边，得到这个分支的黑色节点数作为参考

check函数

1.传入参考黑色节点个数

2.计数每一分支的黑色节点数，递归到底部，可对照节点数是否满足

3.递归遍历看看有没有连续的红色节点

private: 
bool check(Node* root, size_t& reference, size_t num)
{
	if (root == nullptr)
	{
		if (num != reference)
		{
			cout << "路径长度有问题" << endl;
			return false;
		}

		return true;
	}
			

	if (root->_col == Red && root->_parent && root->_parent->_col == Red)
	{
		cout << "节点连续红色" << endl;
		return false;
	}
	
	if (root->_col == Black)
		num++;

	return check(root->_left, reference, num) && check(root->_right, reference, num);
}

bool _Inspect(Node* root)
{
	//空树也是红黑树
	if (_root == nullptr)
		return true;

	//检测根节点是否为黑色
	if (_root->_col != Black)
	{
		cout << "根节点是红色的" << endl;
		return false;
	}
			
	size_t leftNum = 0;
	Node* cur = _root;
	while (cur)
	{
		if (cur->_col == Black)
				leftNum++;
			cur = cur->_left;
	}
	//检测所有路径黑色节点的数量是否一样
	//检测相邻节点是不是都是红色的
	return check(_root, leftNum, 0);
}

3.代码实现

#pragma once
#include<iostream>
#include<assert.h>
#include <stdlib.h>
#include<time.h>
using namespace std;

enum Color
{
	Black,
	Red,
};

template<class K, class V>
struct BRTreeNode
{
	pair<K, V> _kv;
	BRTreeNode* _left;
	BRTreeNode* _right;
	BRTreeNode* _parent;
	Color _col;

	BRTreeNode(const pair<K, V>& kv)
		:_kv(kv)
		, _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _col(Red)
	{}
};

template<class K, class V>
class BRTree
{
public:
	typedef BRTreeNode<K, V> Node;
	bool Insert(const pair<K, V>& kv)
	{
		if (_root == nullptr)
		{
			_root = new Node(kv);
			_root->_col = Black;
			return true;
		}

		//父子节点确定插入的位置
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_kv.first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
				return false;
		}

		//走到这cur就是要插入的位置
		//cur要连接parent，parent也要连接cur---判断靠kv的大小
		cur = new Node(kv);
		if (parent->_kv.first > cur->_kv.first)
		{
			parent->_left = cur;
			cur->_parent = parent;
		}
		else
		{
			parent->_right = cur;
			cur->_parent = parent;
		}

		while (parent && parent->_col == Red)
		{
			Node* grandparent = parent->_parent;
			//parent分在grandparent左右
			if (grandparent->_left == parent)
			{
				//关键是看uncle节点不存在/红色/黑色的情况
				Node* uncle = grandparent->_right;
				//1.uncle红
				//parent和uncle变黑，grandparent变红
				//grandparent变红需要往上判断
				if (uncle && uncle->_col == Red)
				{
					grandparent->_col = Red;
					parent->_col = uncle->_col = Black;

					cur = grandparent;
					parent = cur->_parent;
				}
				else  //uncle不存在/黑色
				{
					//2.cur也是parent的左边，uncle不存在/黑色
					//右旋grandparents，parent变黑，
					if (cur == parent->_left)
					{
						_RotateR(grandparent);
						parent->_col = Black;
						grandparent->_col = Red;
					}
					//3.cur是parent的右边，uncle不存在/黑色
					//左旋parent再右旋grandparents,cur变黑，grandparents变红
					else
					{
						_RotateL(parent);
						_RotateR(grandparent);
						cur->_col = Black;
						grandparent->_col = Red;
					}

					//抽象树的头被设置为黑色，对上面没有影响，所以不需要进行循环
					break;
				}
				
			}
			else
			{
				Node* uncle = grandparent->_left;

				//1.uncle红
				//parent和uncle变黑，grandparent变红
				//grandparent变红需要往上判断
				if (uncle && uncle->_col == Red)
				{
					grandparent->_col = Red;
					parent->_col = uncle->_col = Black;

					cur = grandparent;
					parent = cur->_parent;
				}
				else  //uncle不存在/黑色
				{
					//2.cur也是parent的右边，uncle不存在/黑色
					//左旋grandparents，parent变黑，
					if (cur == parent->_right)
					{
						_RotateL(grandparent);
						parent->_col = Black;
						grandparent->_col = Red;
					}
					//3.cur是parent的右边，uncle不存在/黑色
					//右旋parent再左旋grandparents,cur变黑，grandparents变红
					else
					{
						_RotateR(parent);
						_RotateL(grandparent);
						cur->_col = Black;
						grandparent->_col = Red;
					}

					//抽象树的头被设置为黑色，对上面没有影响，所以不需要进行循环
					break;
				}
			}
		}
		_root->_col = Black;
		return true;
	}

	void Print()
	{
		_Print(_root);
		cout << endl;
	}

	bool Inspect()
	{
		return _Inspect(_root);
	}

private: 
	bool check(Node* root, size_t& reference, size_t num)
	{
		if (root == nullptr)
		{
			if (num != reference)
			{
				cout << "路径长度有问题" << endl;
				return false;
			}

			return true;
		}
			

		if (root->_col == Red && root->_parent && root->_parent->_col == Red)
		{
			cout << "节点连续红色" << endl;
			return false;
		}
		
		if (root->_col == Black)
			num++;

		return check(root->_left, reference, num) && check(root->_right, reference, num);
	}

	bool _Inspect(Node* root)
	{
		//空树也是红黑树
		if (_root == nullptr)
			return true;

		//检测根节点是否为黑色
		if (_root->_col != Black)
		{
			cout << "根节点是红色的" << endl;
			return false;
		}
			
		size_t leftNum = 0;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_col == Black)
				leftNum++;
			cur = cur->_left;
		}
		//检测所有路径黑色节点的数量是否一样
		//检测相邻节点是不是都是红色的
		return check(_root, leftNum, 0);
	}

	void _Print(Node*& cur)
	{
		if (cur == nullptr)
			return;
		_Print(cur->_left);
		cout << cur->_kv.first << " ";
		_Print(cur->_right);
	}

	void _RotateL(Node*& parent)
	{
		Node* pparent = parent->_parent;
		Node* SubR = parent->_right;
		Node* SubRL = SubR->_left;
		if (pparent == nullptr)
		{
			_root = SubR;
			SubR->_parent = nullptr;
		}
		else
		{
			if (pparent->_left == parent)
				pparent->_left = SubR;
			else
				pparent->_right = SubR;
			SubR->_parent = pparent;
		}
		parent->_parent = SubR;
		SubR->_left = parent;
		parent->_right = SubRL;
		if (SubRL != nullptr)
			SubRL->_parent = parent;
	}

	void _RotateR(Node*& parent)
	{
		Node* pparent = parent->_parent;
		Node* SubL = parent->_left;
		Node* SubLR = SubL->_right;
		if (pparent == nullptr)
		{
			_root = SubL;
			SubL->_parent = nullptr;
		}
		else
		{
			if (pparent->_left == parent)
				pparent->_left = SubL;
			else
				pparent->_right = SubL;
			SubL->_parent = pparent;
		}
		parent->_parent = SubL;
		SubL->_right = parent;
		parent->_left = SubLR;
		if (SubLR != nullptr)
			SubLR->_parent = parent;
	}

	Node* _root = nullptr;
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/449303.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【开发经验】spring事件监听机制关心的同步、异步、事务问题

【开发经验】spring事件监听机制关心的同步、异步、事务问题

文章目录 spring发布订阅示例同步核心源码分析如何配置异步事务问题 观察者模式又称为发布订阅模式&#xff0c;定义为&#xff1a;对象间的一种一对多的依赖关系&#xff0c;当一个对象的状态发生改变时&#xff0c;所有依赖它的对象都得到通知并被自动更新。 如下图所示&…
阅读更多...
【Go】六、并发编程

【Go】六、并发编程

文章目录 并发编程1、并发介绍2、Goroutine3、runtime包 3、Channel3.1、channel相关信息 4、Goroutine池&#xff08;❌&#xff09;5、定时器6、select多路复用7、并发安全和锁8、Sync9、原子操作&#xff08;atomic包&#xff09; 并发编程 1、并发介绍 1、进程和线程 ​…
阅读更多...
心塞，被面试官在朋友圈吐槽了

心塞，被面试官在朋友圈吐槽了

​前阵子一个后辈小学弟向我诉苦&#xff0c;说自己在参加某大厂测试的时候被面试官怼得哑口无言&#xff0c;场面让他一度十分尴尬。 印象最深的就是下面几个问题&#xff1a; 自动化测试中&#xff0c;如何解决Case依赖&#xff1f;你们公司业务中&#xff0c;自动化和手工分…
阅读更多...
“五一”预订量创5年新高！如何制定营销活动引爆门店客流？

“五一”预订量创5年新高！如何制定营销活动引爆门店客流？

作为疫情3年经济复苏后&#xff0c;2023年的第一个长假&#xff0c;今年“五一”的消费需求将全面集中释放&#xff0c;带动全国各地线下实体生意全面复苏。 根据官方平台发布的数据显示&#xff0c;今年五一的旅游订单比疫情前的2019年增长了200%&#xff0c;是近5年预订量最多…
阅读更多...
Spring Security 整体架构

Spring Security 整体架构

Spring Security 整体架构 整体架构 在的架构设计中&#xff0c;认证 和 授权 是分开的&#xff0c;无论使用什么样的认证方式。都不会影响授权&#xff0c;这是两个独立的存在&#xff0c;这种独立带来的好处之一&#xff0c;就是可以非常方便地整合一些外部的解决方案。 认…
阅读更多...
（数字图像处理MATLAB+Python）第五章图像增强-第三节：基于照度反射模型的图像增强

（数字图像处理MATLAB+Python）第五章图像增强-第三节：基于照度反射模型的图像增强

文章目录 一&#xff1a;基于同态滤波的增强&#xff08;1&#xff09;概述&#xff08;2&#xff09;程序 二&#xff1a;Retinex理论&#xff08;1&#xff09;Retinex理论概述&#xff08;1&#xff09;SSR&#xff08;单尺度Retinex 算法&#xff09;&#xff08;2&#xf…
阅读更多...
Oracle的学习心得和知识总结（二十二）|Oracle数据库Real Application Testing之Database Replay实操(二)

Oracle的学习心得和知识总结（二十二）|Oracle数据库Real Application Testing之Database Replay实操(二)

目录结构 注&#xff1a;提前言明 本文借鉴了以下博主、书籍或网站的内容&#xff0c;其列表如下&#xff1a; 1、参考书籍&#xff1a;《Oracle Database SQL Language Reference》 2、参考书籍&#xff1a;《PostgreSQL中文手册》 3、EDB Postgres Advanced Server User Gui…
阅读更多...
操作系统概述及Linux基本指令（1）

操作系统概述及Linux基本指令（1）

目录 一. 操作系统 1.1 什么是操作系统 1.2 操作系统的核心工作 二. Linux的基本指令 2.1 ls指令 -- 打印文件名 2.2 pwd指令 -- 显示路径 2.3 cd指令 -- 进入特定目录 2.4 touch指令 -- 创建普通文件 2.5 mkdir指令 -- 创建路径 2.6 rmdir/rm指令 -- 删除路径或普通…
阅读更多...
【GeoDjango框架解析】空间方法的ORM查询

【GeoDjango框架解析】空间方法的ORM查询

原文作者&#xff1a;我辈理想 版权声明&#xff1a;文章原创&#xff0c;转载时请务必加上原文超链接、作者信息和本声明。 Django数据操作-ORM 第一章 【Django开发入门】ORM的增删改查和批量操作 第二章 【Django开发入门】ORM查询分页以及返回Json格式 文章目录 Django数据…
阅读更多...
中国人民大学与加拿大女王大学金融硕士——在职读研该如何平衡学习与工作呢

中国人民大学与加拿大女王大学金融硕士——在职读研该如何平衡学习与工作呢

边工作边考研&#xff0c;对于所有人来说都是个不小的挑战&#xff0c;每年都有大量在职生因为焦躁、压力而中途离场。学习时间碎片化&#xff0c;复习进度特别容易被工作上的事情所打断&#xff0c;再想“重新启动”就会很难。想要节省备考时间建议你读免联考的中外合作办学项…
阅读更多...
基于Canvas实现图片的上传和渲染

基于Canvas实现图片的上传和渲染

1 Canvas 1.1 什么是Canvas 是一个可以使用脚本 (通常为JavaScript) 来绘制图形的 HTML 元素。例如&#xff0c;它可以用于绘制图表、制作图片构图或者制作简单的动画。 1.2 基本使用 宽高&#xff1a; <canvas id"tutorial" width"150" height&qu…
阅读更多...
＜C++＞C++入门

＜C++＞C++入门

目录 前言 一、C关键字&#xff08;C98&#xff09; 二、命名空间 1. 命名空间定义 2. 命名空间的使用 3. 命名空间的使用有三种方式&#xff1a; 三、C输入&输出 四、缺省参数 1. 缺省参数概念 2. 缺省参数的分类 3. 缺省参数的应用 五、函数重载 六、引用 1. 引用的概念…
阅读更多...
web实验（2）

web实验（2）

&#xff08;1&#xff09; 应用html标签和css完成如下所示页面效果&#xff0c;图片见附件。 说明&#xff1a; 内容相对于浏览器居中,宽860px鼠标移动至列表项上&#xff0c;显示背景色#F8F8F8分割线2px solid #ccc&#xff0c;每项高130px第一行文字&#xff1a;20px 黑体…
阅读更多...
4.功能权限

4.功能权限

基于角色的权限控制&#xff0c;用户分配角色&#xff0c;角色分配菜单。 1. 权限注解 1.基于【权限标识】的权限控制 权限标识&#xff0c;对应 system_menu 表的 permission 字段&#xff0c;推荐格式为 {系统}:{模块}:{操作}&#xff0c;例如说 system:admin:add 标识 sy…
阅读更多...
chatgpt智能提效职场办公-ppt怎么做才好看又快

chatgpt智能提效职场办公-ppt怎么做才好看又快

作者&#xff1a;虚坏叔叔 博客&#xff1a;https://xuhss.com 早餐店不会开到晚上&#xff0c;想吃的人早就来了&#xff01;&#x1f604; 制作ppt有几个方面可以考虑&#xff0c;以实现既好看又快速的目的&#xff1a; 使用模板&#xff1a;使用ppt模板可以更快速地制作出一…
阅读更多...
JavaScript概述二(Date+正则表达式+Math+函数+面向对象)

JavaScript概述二(Date+正则表达式+Math+函数+面向对象)

1.Date 1.1 new一个Date对象表示当前系统时间 var nownew Date(); console.log(now);1.2 根据传入的时间格式表示时间 var date1new Date(2023-4-20 00:16:40); console.log(date1); 1.3 传入时间毫秒数&#xff0c;返回从1900年1月1日8时&#xff08;东八区&#xff09;X分X…
阅读更多...
C语言入门篇——操作符篇

C语言入门篇——操作符篇

目录 1、操作符分类 2、操作符的属性 3、算术操作符 4、移位操作符 5、位操作符 6、赋值操作符 7、单目操作符 8、关系操作符 9、逻辑操作符 10、条件操作符 11、逗号操作符 12、下标引用、函数调用和结构成员 1、操作符分类 算术操作符&#xff08;&#xff0c;-&…
阅读更多...
办公必备！不再被格式问题困扰，轻松搞定文档转换！

办公必备！不再被格式问题困扰，轻松搞定文档转换！

大家平时在工作中会需要将文档转换为其他格式吗&#xff1f; 日常工作中&#xff0c;经常碰到需要文件格式转换的情况&#xff0c;对于掌握了一些转换技能的朋友说&#xff0c;文件格式转换自然不在话下 对于不熟练的朋友来说&#xff0c;想要轻松转换文件格式&#xff0c;就…
阅读更多...
c++ std::enable_shared_from_this作用

c++ std::enable_shared_from_this作用

enable_shared_from_this 是什么 std::enable_shared_from_this 是一个类模板&#xff0c;用来返回指向当前对象的shared_ptr智能指针。在说明它的作用前我们可以看一下如下代码&#xff1a; demo.cpp #include <memory> #include <iostream>class A { public:A…
阅读更多...
web实验（3）

web实验（3）

应用JavaScript编写留言的功能&#xff0c;在文本中输入文字提交后&#xff0c;在下方进行显示。 提示&#xff1a;可将下方内容以列表体现&#xff0c;提交时动态创建列表的项。可使用以下两种方式之一的方法&#xff1a; 使用CreateElenment动态创建li标签及li中的文本 在列…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023