一、最长公共子序列问题
1、问题概念
一个序列的子序列是在该序列中删去若干元素后得 到的序列。
例如:"ABCD”和“BDF”都是“ABCDEFG”的子序列。
最长公共子序列(LCS) 问题: 给定两个序列X和Y,求X和Y长度最大的公共子字列。
例:X="ABBCBDE”Y="DBBCDB”LCS(XY)="BBCD"
应用场景:字符串相似度比对
2、问题求解思路
(1)问题思考
思考: 暴力穷举法的时间复杂度是多少?
序列中的每一个值都有两种选择,被选择或者不被选择,因此一个长度为n的序列,其子序列为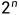 种。求解长度为n和长度为m的序列的公共子序列,对比
种。求解长度为n和长度为m的序列的公共子序列,对比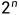 和
和 个子序列之间的关系,是否相同,因此时间复杂度为O(
个子序列之间的关系,是否相同,因此时间复杂度为O( )。
)。
思考: 最长公共子序列是否具有最优子结构性质?
有,见解最优子结构
(2)最优子结构
(LCS的最优子结构):令X=(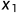 ,
,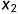 ,......,
,......,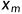 )和Y=(
)和Y=( ,
, ,......,
,......,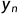 )为两个序列,Z=(
)为两个序列,Z=(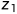 ,
,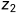 ,......,
,......,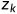 )为X和Y的任意 LCS。
)为X和Y的任意 LCS。
如果
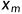 =
= 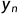 ,则
,则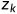 =
= 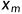 =
= 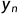 且
且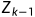 是
是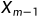 和
和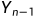 的一个LCS。
的一个LCS。
例如:序列ABCD和ABD,其LCS为ABD,此时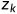 =
= 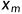 =
= 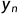 =D,可见,AB是ABC和AB的LCS。
=D,可见,AB是ABC和AB的LCS。
如果
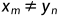 ,且
,且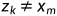 意味着Z是
意味着Z是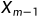 和Y的一个LCS。
和Y的一个LCS。
例如:序列ABCD和ABC,其LCS为ABC,此时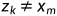 ,即D与C不相等,则
,即D与C不相等,则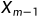 为ABC,可见,ABC是ABC和ABC的LCS。
为ABC,可见,ABC是ABC和ABC的LCS。
如果
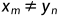 ,且
,且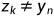 意味着Z是X和
意味着Z是X和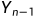 的一个LCS。
的一个LCS。
例如:序列ABC和ACD,其LCS为AC,此时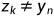 ,即D与C不相等,则
,即D与C不相等,则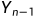 为AC,可见,AC是ABC和AC的LCS。
为AC,可见,AC是ABC和AC的LCS。
示例如下:
要求a="ABCBDAB"与b="BDCABA"的LCS:
由于最后一位"B“≠"A”:
因此LCS(a,b)应该来源于LCS(a[:-1],b)与LCS(a,b[:-1])中更大的那一个
(3)问题递推式
1)递推式推理说明
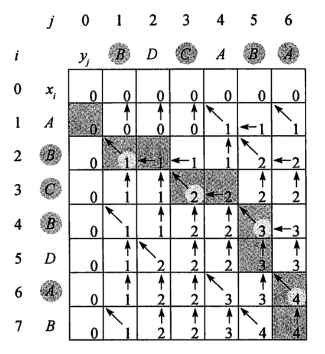
结合最优子结构的定理,可以得到以上的图。
举例解析:
x0都是空列表,y0也是空列表,因此与x0或者y0的LCS一定是0。
序列BDC和序列A:C != A,则LCS来源与LCS([BDC],[ ])和LCS([BD],[A])中,图中可看出,两者都为0,即LCS([BDC], [A])的左边和上边的位置。
序列BDCA和序列A:A = A,则A一定是两个序列的LCS中的一个元素,且LCS([BDC], [A])加上元素A就是LCS([BDCA], [A])。查看可知,LCS([BDC], [A]) = 0,所以LCS([BDCA], [A]) = 0 + 1(元素A)。
剩余的同理。
2)递推式
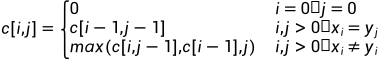
c[i,j]表示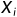 和
和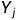 的LCS长度
的LCS长度
二、最长公共子序问题代码实现
1、最长公共子序长度求解
def lcs_length(x,y): # 公共子序列长度,x,y: 字符串、列表等序列
m = len(x) # x序列长度
n = len(y) # y序列长度
c = [[0 for i in range(n + 1)] for _ in range(m+1)] # 创建m行n列二维数组,初始值为0
for i in range(1, m+1): # 按数组的行求,x0都为0不用求,所以从1开始
for j in range(1, n+1): # 数组每行中的遍历,y0都为0,不用求
if x[i - 1] == y[j - 1]: # x[i-1]其实是字符串的i,因为i=0在二维列表中都是0,不求解,但是在字符串中仍需要从索引0遍历
c[i][j] = c[i-1][j-1] + 1 # 递推式
else: # xi!=yi
c[i][j] = max(c[i-1][j],c[i][j-1]) # 递推式
return c[m][n] # x和y的最后一个元素对比完,二维数组的最后一位
print(lcs_length('ABCBDAB', 'BDCABA'))输出结果
42、最长公共子序的序列求解
动态规划+ 回溯算法搭配使用,动态规划求解最优值,回溯法推算出过程的解。
(1)动态规划求解并存储解-代码实现
# 动态规划求解,存储解及解的计算过程
def lcs(x,y): # 求解并存储箭头方向,x,y为字符串、列表等序列
m = len(x) # x的长度
n = len(y) # y的长度
c = [[0 for i in range(n+1)] for _ in range(m+1)] # 二维数组,初始值为0,用于存储长度结果
d = [[0 for i in range(n+1)] for _ in range(m+1)] # 二维数组,初始值为0,用于存储箭头方向,1表示左上,2表示上,3表示左
for i in range(1,m+1): # 按行遍历二维数组
for j in range(1,n+1): # 每行的各数值遍历, c0j和ci0相关的值都为0,所以均从1开始
if x[i - 1] == y[j - 1]: # xi=yi的情况,二维数组中i,j=0时,都为0已经确定,但字符串x,y仍需从0开始遍历
c[i][j] = c[i - 1][j - 1] + 1 # 递推式
d[i][j] = 1 # 箭头方向左上方
elif c[i][j - 1] > c[i - 1][j]: # 递推式,选择更大的
c[i][j] = c[i][j - 1]
d[i][j] = 3 # 箭头左边
else: # c[i-1][j] >= c[i][j-1]
c[i][j] = c[i - 1][j]
d[i][j] = 2 # 箭头上方
return c[m][n], d
c, d = lcs("ABCBDAB", "BDCABA")
for _ in d:
print(_)输出结果:
[0, 0, 0, 0, 0, 0, 0]
[0, 2, 2, 2, 1, 3, 1]
[0, 1, 3, 3, 2, 1, 3]
[0, 2, 2, 1, 3, 2, 2]
[0, 1, 2, 2, 2, 1, 3]
[0, 2, 1, 2, 2, 2, 2]
[0, 2, 2, 2, 1, 2, 1]
[0, 1, 2, 2, 2, 1, 2](2)回溯算法的应用-代码实现
# 动态规划求解,存储解及解的计算过程
def lcs(x,y): # 求解并存储箭头方向,x,y为字符串、列表等序列
m = len(x) # x的长度
n = len(y) # y的长度
c = [[0 for i in range(n+1)] for _ in range(m+1)] # 二维数组,初始值为0,用于存储长度结果
d = [[0 for i in range(n+1)] for _ in range(m+1)] # 二维数组,初始值为0,用于存储箭头方向,1表示左上,2表示上,3表示左
for i in range(1,m+1): # 按行遍历二维数组
for j in range(1,n+1): # 每行的各数值遍历, c0j和ci0相关的值都为0,所以均从1开始
if x[i - 1] == y[j - 1]: # xi=yi的情况,二维数组中i,j=0时,都为0已经确定,但字符串x,y仍需从0开始遍历
c[i][j] = c[i - 1][j - 1] + 1 # 递推式
d[i][j] = 1 # 箭头方向左上方
elif c[i][j - 1] > c[i - 1][j]: # 递推式,选择更大的
c[i][j] = c[i][j - 1]
d[i][j] = 3 # 箭头左边
else: # c[i-1][j] >= c[i][j-1]
c[i][j] = c[i - 1][j]
d[i][j] = 2 # 箭头上方
return c[m][n], d
# 回溯算法
def lcs_trackback(x,y): # 最长公共子序列的序列
c, d = lcs(x, y) # c长度,d箭头方向
i = len(x) # x的长度
j = len(y) # y的长度
res = [] # 结果列表
while i > 0 and j > 0 : # 序列x和y还有值未比对,任何一个序列为0了都不再继续
if d[i][j] == 1: # 箭头左上方 ——> 匹配
res.append(x[i - 1]) # 二维列表中i=0时,值为0,但是序列x的值是从0开始遍历的
i = i - 1 # 位置移到左上位置
j = j - 1
elif d[i][j] == 2: # 箭头上方->不匹配
i = i - 1 # 位置往上移一格
else: # dij = 3 ,箭头左向
j = j - 1 # 位置往左移一格
return "".join(reversed(res)) # 列表翻转,并将列表用''连接成字符串
print(lcs_trackback("ABCBDAB", "BDCABA"))结果输出
BCBA