文章目录
- 一:基于同态滤波的增强
- (1)概述
- (2)程序
- 二:Retinex理论
- (1)Retinex理论概述
- (1)SSR(单尺度Retinex 算法)
- (2)MSR(多尺度Retinex算法)
基于照度反射模型的图像增强:基于照度反射模型的图像增强方法是通过对图像中的亮度和对比度进行调整来改善图像质量。该方法假设图像的亮度可以分解为照度和反射两个部分,其中照度是由光源产生的光照强度分布,而反射是由物体表面的反射率和光照强度共同决定的
- i ( x , y ) i (x, y) i(x,y) 描述景物照明的缓慢变换,近似为低频分量
- r ( x , y ) r (x, y) r(x,y)描述景物内容的快速变化,近似为高频分量
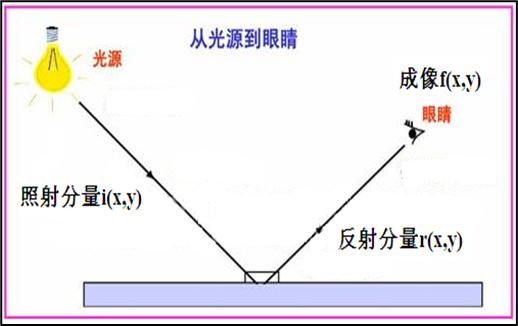
基于照度反射模型的图像增强方法主要包括以下步骤
- 估计图像的照度分布:这一步骤旨在将图像中的照度分离出来,以便后续对反射分布进行调整。常用的方法包括基于直方图均衡化的方法、基于高斯模型的方法、以及基于Retinex理论的方法等
- 计算图像的反射分布:在得到照度分布后,可以通过将原始图像除以照度分布得到反射分布,反射分布代表了物体表面的反射率信息
- 调整图像的反射分布:可以通过对反射分布进行线性或非线性变换来调整图像的对比度和亮度,以改善图像的质量。常用的方法包括伽马校正、对数变换、以及直方图匹配等
- 将调整后的反射分布与照度分布相乘,得到增强后的图像
一:基于同态滤波的增强
(1)概述
- 背景:若物体受到照度明暗不匀的时候,图像上对应照度暗的部分,其细节就较难辨别
- 主要目的:消除不均匀照度的影响,增强图像细节
基于同态滤波的增强:是一种可以有效提高图像质量的方法,其主要思想是将图像转换到频域进行处理,通过调整图像在频域中的幅度和相位信息来实现增强。具体来说,基于同态滤波的图像增强可以通过以下公式表示:
g ( x , y ) = H ( u , v ) F ( u , v ) g(x,y) = H(u,v)F(u,v) g(x,y)=H(u,v)F(u,v)
其中, g ( x , y ) g(x,y) g(x,y) 表示增强后的图像, F ( u , v ) F(u,v) F(u,v) 表示原始图像在频域中的傅里叶变换, H ( u , v ) H(u,v) H(u,v) 是滤波器函数,用于调整图像在频域中的幅度和相位信息, u u u 和 v v v 分别表示频域中的横向和纵向坐标
同态滤波器的具体形式可以表示为:
H ( u , v ) = H l p ( u , v ) H h p ( u , v ) H(u,v) = H_{lp}(u,v)H_{hp}(u,v) H(u,v)=Hlp(u,v)Hhp(u,v)
其中, H l p ( u , v ) H_{lp}(u,v) Hlp(u,v) 和 H h p ( u , v ) H_{hp}(u,v) Hhp(u,v) 分别表示低通和高通滤波器,用于调整图像在频域中的低频和高频信息。一般情况下, H l p ( u , v ) H_{lp}(u,v) Hlp(u,v) 采用高斯滤波器, H h p ( u , v ) H_{hp}(u,v) Hhp(u,v) 采用巴特沃斯滤波器。在进行同态滤波时,可以将图像进行对数变换,将乘法操作转换为加法操作,从而简化计算。最后,通过将增强后的图像进行反变换,即可得到在空域中增强后的图像
(2)程序

matlab实现:
Image=double(rgb2gray(imread('gugong1.jpg'))); %打开图像并转换为double数据
imshow(uint8(Image)),title('故宫');
logI=log(Image+1); %对数运算
sigma=1.414; filtersize=[7 7]; %高斯滤波器参数
lowfilter=fspecial('gaussian',filtersize,sigma); %构造高斯低通滤波器
highfilter=zeros(filtersize);
highpara=1; lowpara=0.4; %控制滤波器幅度范围的系数
highfilter(ceil(filtersize(1,1)/2),ceil(filtersize(1,2)/2))=1;
highfilter=highpara*highfilter-(highpara-lowpara)*lowfilter; %高斯低通滤波器转换为高斯高通滤波器
highpart=imfilter(logI,highfilter,'replicate','conv'); %时域卷积实现滤波
NewImage=exp(highpart); %指数变换恢复图像
top=max(NewImage(:)); bottom=min(NewImage(:));
NewImage=(NewImage-bottom)/(top-bottom); %数据的映射处理,符合人眼视觉特性
NewImage=1.5.*(NewImage);
figure,imshow((NewImage));title('基于同态滤波的增强图像');
imwrite(NewImage,'tongtai.bmp');
python实现:
import cv2
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
# 读取图像并转换为double数据类型
img = cv2.imread('gugong1.jpg')
img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY).astype(np.float64)
# 显示原始图像
plt.imshow(img, cmap='gray')
plt.title('故宫')
plt.show()
# 对图像进行对数变换
log_img = np.log(img + 1)
# 构造高斯低通滤波器
sigma = 1.414
filter_size = (7, 7)
low_filter = cv2.getGaussianKernel(filter_size[0], sigma)
low_filter = low_filter @ low_filter.T
# 构造高斯高通滤波器
high_filter = np.zeros(filter_size)
high_para = 1
low_para = 0.4
high_filter[filter_size[0] // 2, filter_size[1] // 2] = 1
high_filter = high_para * high_filter - (high_para - low_para) * low_filter
# 对图像进行高斯高通滤波
high_part = cv2.filter2D(log_img, -1, high_filter, borderType=cv2.BORDER_REPLICATE)
# 进行指数变换并进行数据映射
new_img = np.exp(high_part)
new_img = (new_img - np.min(new_img)) / (np.max(new_img) - np.min(new_img))
new_img = 1.5 * new_img
# 显示增强后的图像并保存
plt.imshow(new_img, cmap='gray')
plt.title('基于同态滤波的增强图像')
plt.show()
cv2.imwrite('tongtai.bmp', new_img * 255)
二:Retinex理论
(1)Retinex理论概述
Retinex理论:是由美国斯坦福大学的Edwin H. Land教授于1971年提出的一种图像处理理论。Retinex是一个合成词,它的构成是retina(视网膜)+cortex(皮层)→ Retinex。多年来Retinex算法,从单尺度Retinex算法( SSR)改进成多尺度加权平均的Retinex算法(MSR),再发展成带彩色恢复的多尺度Retinex算法( MSRCR)。 尽管这些算法不尽相同,但其基本原理都非常相似,都是通过对原始图像进行高斯滤波来获取照度图像,并尽量准确的获取照度图像,最后将照度图像从原始图像中分离出来,从而获得反射图像。Retinex模型的理论基础是三色理论和颜色恒常性,即物体的颜色是由物体对长波(红色)、中波(绿色)、短波(蓝色)光线的反射能力来决定的,而不是由反射光强度的绝对值来决定的,物体的色彩不受光照非均匀性的影响,具有一致性,即Retinex是以色感一致性(颜色恒常性)为基础的。该理论的核心论点如下
- 人眼对物体颜色的感知与物体表面的反射性质有着密切关系,即反射率低的物体看上去较暗,反射率高的物体看上去是较亮
- 人眼对物体色彩的感知具有一致性,不受光照变化的影响
Retinex理论认为图像 I ( x , y ) I(x,y) I(x,y)是由照度图像与反射图像组成,如下,根据照度-反射模型,Retinex理论中的核心方程式为
- R ( x , y ) R(x,y) R(x,y)表示物体反射信息
- L ( x , y ) L(x,y) L(x,y)表示入射分量信息
I ( x , y ) = R ( x , y ) ∗ L ( x , y ) I(x,y)=R(x,y)*L(x,y) I(x,y)=R(x,y)∗L(x,y)

Retinex理论发展历程如下,大致经历两个阶段
- 基于迭代的Retinex算法(存在很大缺陷)
- 基于中心环绕的Retinex算法
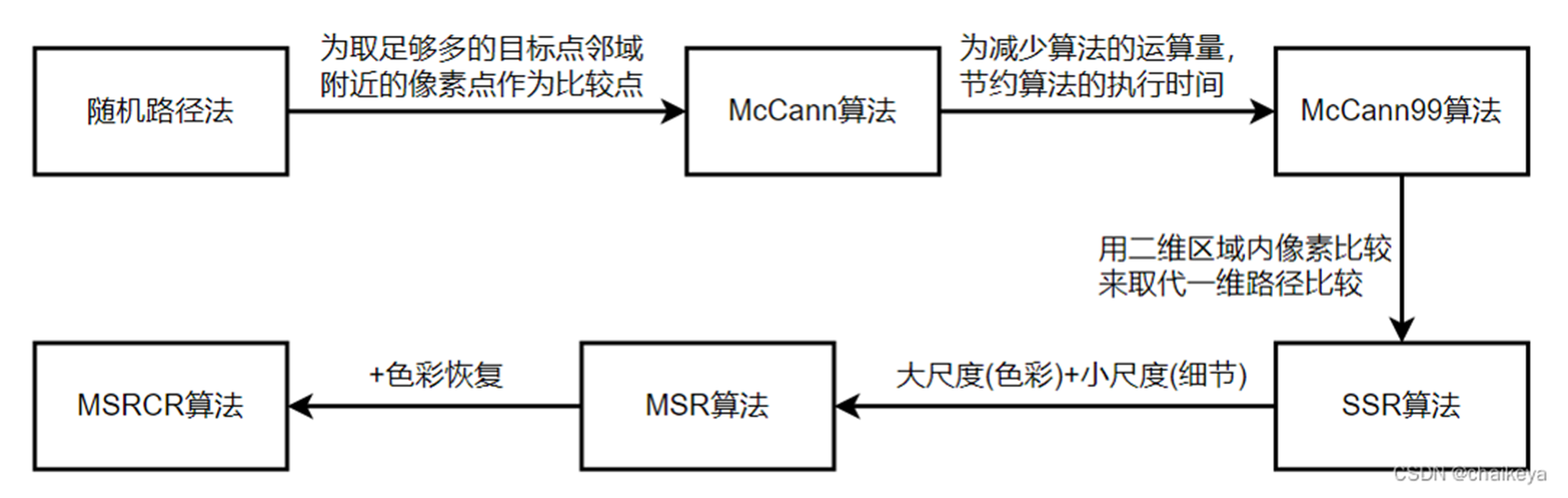
(1)SSR(单尺度Retinex 算法)
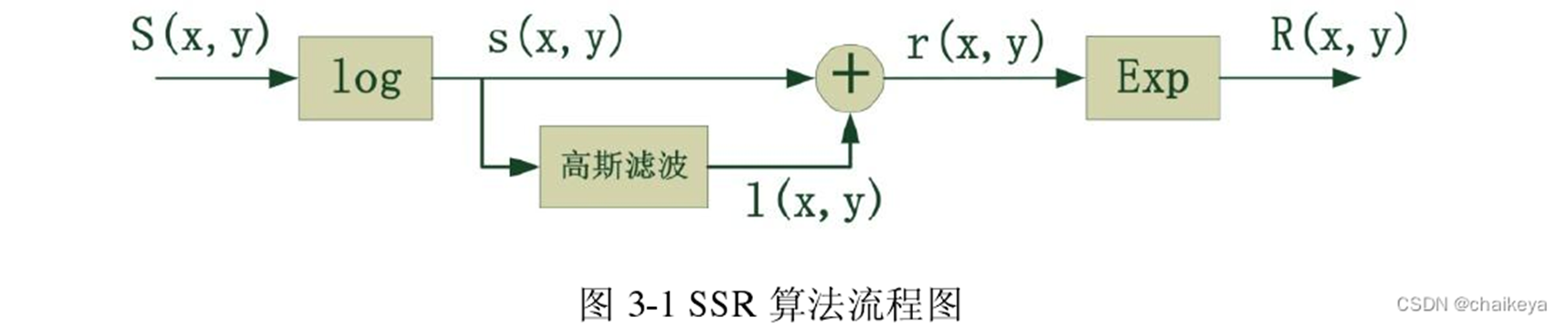
SSR:是一种基于Retinex的图像增强算法,仅针对单一尺度操作,算法步骤如下
- 读取原图像数据 S ( x , y ) S(x,y) S(x,y),并将整形转换为double型
- 确定尺度参数 σ \sigma σ的大小,确定满足条件 ∬ G ( x , y ) d x d y = 1 \iint G(x,y)dxdy=1 ∬G(x,y)dxdy=1的 λ \lambda λ值
- 根据公式 r ( x , y ) = log S ( x , y ) − log [ G ( x , y ) ⋅ S ( x , y ) ] r(x,y)=\log S(x,y)-\log[G(x,y)\cdot S(x,y)] r(x,y)=logS(x,y)−log[G(x,y)⋅S(x,y)]求 r ( x , y ) r(x,y) r(x,y)的值
- 将 r ( x , y ) r(x,y) r(x,y)值由对属于转换为实数域 R ( x , y ) R(x,y) R(x,y)
- 对 R ( x , y ) R(x,y) R(x,y)做线性拉伸处理,并输出显示
对于灰度图像来说,直接对灰度值做上述步骤处理即可;对于彩色图像来说,需要分解为R、G、B三幅灰度图然后作上述步骤处理,最后合成为彩色图像
实现如下效果

matlab实现:
clear all;
close all;
clc;
I = imread('origin.jpg');%读图
% 提取原始图像的红色通道,将其转换为双精度类型,并进行log变换和二维傅里叶变换
R = I(:, :, 1);
[N1, M1] = size(R);
R0 = double(R);
Rlog = log(R0+1);
Rfft2 = fft2(R0);
% 设定高斯核参数sigma,并生成与图像大小相同的高斯核。然后将高斯核进行二维傅里叶变换
sigma = 80;
F = fspecial('gaussian', [N1,M1], sigma);
Efft = fft2(double(F));
% 进行卷积操作,然后将该结果进行傅里叶反变换,得到卷积结果的空域图像
DR0 = Rfft2.* Efft;%卷积
DR = ifft2(DR0);%反变换到空域
% 将卷积结果的空域图像进行log变换,然后将其与原始图像的log变换相减,得到增强后的图像的log变换
DRlog = log(DR +1);
Rr = Rlog - DRlog;
% 将卷积结果的空域图像进行log变换,然后将其与原始图像的log变换相减,得到增强后的图像的log变换
EXPRr = Rr;
MIN = min(min(EXPRr));
MAX = max(max(EXPRr));
EXPRr = 255*(EXPRr - MIN)/(MAX - MIN);%线性拉伸
G = I(:, :, 2);
G0 = double(G);
Glog = log(G0+1);
Gfft2 = fft2(G0);
DG0 = Gfft2.* Efft;
DG = ifft2(DG0);
DGlog = log(DG +1);
Gg = Glog - DGlog;
EXPGg = Gg;
MIN = min(min(EXPGg));
MAX = max(max(EXPGg));
EXPGg = 255*(EXPGg - MIN)/(MAX - MIN);
B = I(:, :, 3);
B0 = double(B);
Blog = log(B0+1);
Bfft2 = fft2(B0);
DB0 = Bfft2.* Efft;
DB = ifft2(DB0);
DBlog = log(DB+1);
Bb = Blog - DBlog;
EXPBb = Bb;
MIN = min(min(EXPBb));
MAX = max(max(EXPBb));
EXPBb = 255*(EXPBb - MIN)/(MAX - MIN);
result = cat(3, EXPRr, EXPGg, EXPBb);
subplot(121), imshow(I);
subplot(122), imshow(uint8(result));
python实现:
import cv2
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
# 读取图像
I = cv2.imread('origin.jpg')
# 提取红色通道,将其转换为双精度类型,并进行log变换和二维傅里叶变换
R = I[:, :, 2]
N1, M1 = R.shape
R0 = np.double(R)
Rlog = np.log(R0+1)
Rfft2 = np.fft.fft2(R0)
# 设定高斯核参数sigma,并生成与图像大小相同的高斯核。然后将高斯核进行二维傅里叶变换
sigma = 80
F = cv2.getGaussianKernel(max(N1,M1),sigma)
F = np.outer(F,F)
Efft = np.fft.fft2(np.double(F),[N1,M1])
# 进行卷积操作,然后将该结果进行傅里叶反变换,得到卷积结果的空域图像
DR0 = Rfft2 * Efft
DR = np.fft.ifft2(DR0)
# 将卷积结果的空域图像进行log变换,然后将其与原始图像的log变换相减,得到增强后的图像的log变换
DRlog = np.log(DR + 1)
Rr = Rlog - DRlog
# 线性拉伸像素值到0-255之间
EXPRr = Rr
MIN = np.min(EXPRr)
MAX = np.max(EXPRr)
EXPRr = 255 * (EXPRr - MIN) / (MAX - MIN)
EXPRr = np.uint8(EXPRr)
G = I[:, :, 1]
G0 = np.double(G)
Glog = np.log(G0+1)
Gfft2 = np.fft.fft2(G0)
DG0 = Gfft2 * Efft
DG = np.fft.ifft2(DG0)
DGlog = np.log(DG+1)
Gg = Glog - DGlog
EXPGg = Gg
MIN = np.min(EXPGg)
MAX = np.max(EXPGg)
EXPGg = 255 * (EXPGg - MIN) / (MAX - MIN)
EXPGg = np.uint8(EXPGg)
B = I[:, :, 0]
B0 = np.double(B)
Blog = np.log(B0+1)
Bfft2 = np.fft.fft2(B0)
DB0 = Bfft2 * Efft
DB = np.fft.ifft2(DB0)
DBlog = np.log(DB+1)
Bb = Blog - DBlog
EXPBb = Bb
MIN = np.min(EXPBb)
MAX = np.max(EXPBb)
EXPBb = 255 * (EXPBb - MIN) / (MAX - MIN)
EXPBb = np.uint8(EXPBb)
# 合并增强后的通道,形成增强后的图像
result = cv2.merge((EXPRr, EXPGg, EXPBb))
# 显示原始图像和增强后的图像
fig, ax = plt.subplots(1, 2)
ax[0].imshow(cv2.cvtColor(I, cv2.COLOR_BGR2RGB))
ax[0].set_title('Original Image
(2)MSR(多尺度Retinex算法)
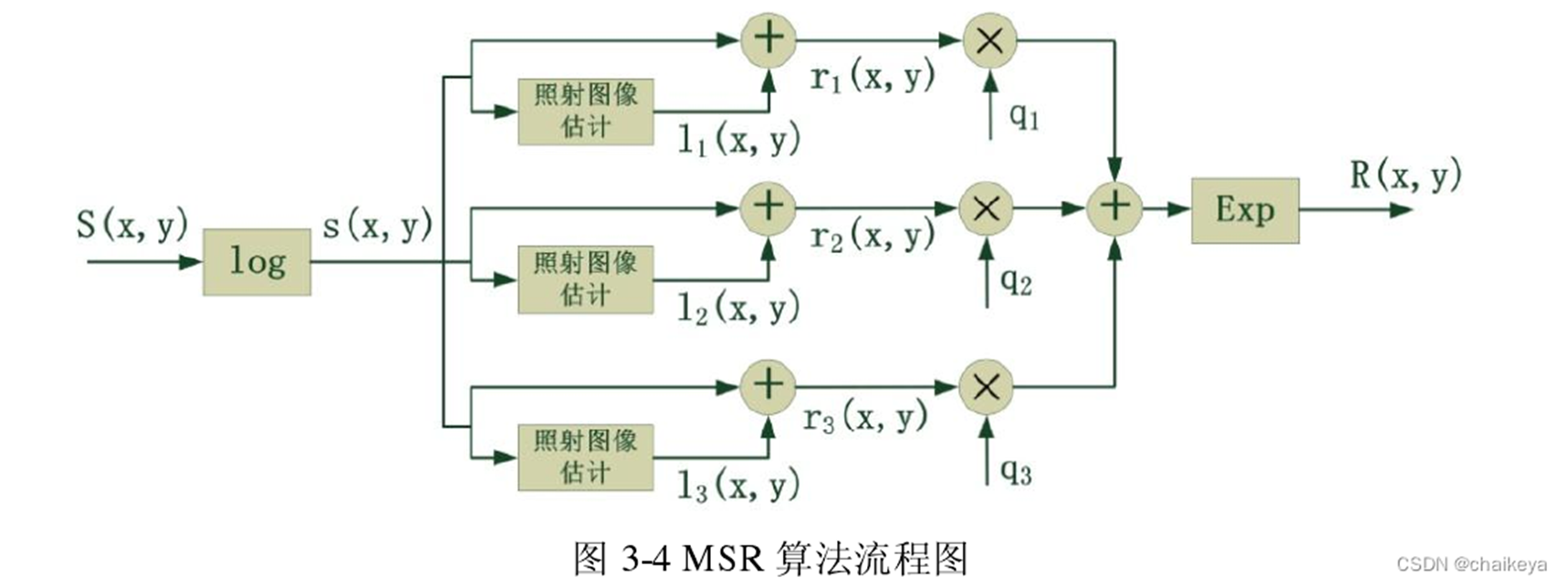
MSR:简单来说,MSR采用几个不同大小的尺度参数对R.G.B三个分量分别单独做滤波后再线性加权归一化就得到了MSR算法。算法步骤如下
- 读取原图像数据 S ( x , y ) S(x,y) S(x,y),并把整型转换为double类型
- 分别确定3个尺度参数 σ 1 , σ 2 . σ 3 \sigma_{1},\sigma_{2}.\sigma_{3} σ1,σ2.σ3大小,确定满足条件 ∬ G k ( x , y ) d x d y = 1 \iint G_{k}(x,y)dxdy=1 ∬Gk(x,y)dxdy=1的 λ 1 , λ 2 , λ 3 \lambda_{1},\lambda_{2},\lambda_{3} λ1,λ2,λ3的值
- 根据公式 r ( x , y ) = ∑ k = 1 K q k { log S ( x , y ) − log [ G k ( x , y ) ∗ S ( x , y ) ] } r(\mathrm{x}, \mathrm{y})=\sum_{k=1}^{K} q_{k}\left\{\log \mathrm{S}(\mathrm{x}, \mathrm{y})-\log \left[\mathrm{G}_{k}(\mathrm{x}, \mathrm{y}) * \mathrm{~S}(\mathrm{x}, \mathrm{y})\right]\right\} r(x,y)=∑k=1Kqk{logS(x,y)−log[Gk(x,y)∗ S(x,y)]}求 r ( x , y ) r(x,y) r(x,y)的值
- 将 r ( x , y ) r(x,y) r(x,y)值由对属于转换为实数域 R ( x , y ) R(x,y) R(x,y)
- 对 R ( x , y ) R(x,y) R(x,y)做线性拉伸处理,并输出显示
实现如下效果

matlab实现:
close all; clear all; clc
I = imread('origin.jpg');
I_r = double(I(:,:,1));
I_g = double(I(:,:,2));
I_b = double(I(:,:,3));
I_r_log = log(I_r+1);
I_g_log = log(I_g+1);
I_b_log = log(I_b+1);
Rfft1 = fft2(I_r);
Gfft1 = fft2(I_g);
Bfft1 = fft2(I_b);[m,n] = size(I_r);
sigma1 = 15;
sigma2 = 80;
sigma3 = 200;
f1 = fspecial('gaussian', [m, n], sigma1);
f2 = fspecial('gaussian', [m, n], sigma2);
f3 = fspecial('gaussian', [m, n], sigma3);
efft1 = fft2(double(f1));
efft2 = fft2(double(f2));
efft3 = fft2(double(f3));
D_r1 = ifft2(Rfft1.*efft1);
D_g1 = ifft2(Gfft1.*efft1);
D_b1 = ifft2(Bfft1.*efft1);
D_r_log1 = log(D_r1 + 1);
D_g_log1 = log(D_g1 + 1);
D_b_log1 = log(D_b1 + 1);
R1 = I_r_log - D_r_log1;
G1 = I_g_log - D_g_log1;
B1 = I_b_log - D_b_log1;
D_r2 = ifft2(Rfft1.*efft2);
D_g2 = ifft2(Gfft1.*efft2);
D_b2 = ifft2(Bfft1.*efft2);
D_r_log2 = log(D_r2 + 1);
D_g_log2 = log(D_g2 + 1);
D_b_log2 = log(D_b2 + 1);
R2 = I_r_log - D_r_log2;
G2 = I_g_log - D_g_log2;
B2 = I_b_log - D_b_log2;
D_r3 = ifft2(Rfft1.*efft3);
D_g3 = ifft2(Gfft1.*efft3);
D_b3 = ifft2(Bfft1.*efft3);
D_r_log3 = log(D_r3 + 1);
D_g_log3 = log(D_g3 + 1);
D_b_log3 = log(D_b3 + 1);
R3 = I_r_log - D_r_log3;
G3 = I_g_log - D_g_log3;
B3 = I_b_log - D_b_log3;
R = 0.1*R1 + 0.4*R2 + 0.5*R3;
G = 0.1*G1 + 0.4*G2 + 0.5*G3;
B = 0.1*B1 + 0.4*B2 + 0.5*B3;
R = exp(R);
MIN = min(min(R));
MAX = max(max(R));
R = (R - MIN)/(MAX - MIN);
R = adapthisteq(R);
G = exp(G);
MIN = min(min(G));
MAX = max(max(G));
G = (G - MIN)/(MAX - MIN);
G = adapthisteq(G);
B = exp(B);
MIN = min(min(B));
MAX = max(max(B));
B = (B - MIN)/(MAX - MIN);
B = adapthisteq(B);
J = cat(3, R, G, B);
figure;
subplot(121);imshow(I);
subplot(122);imshow(J,[]);
python实现:
import cv2
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
# 读取图像
I = cv2.imread('origin.jpg')
# 将图像拆分为R,G,B通道
I_r = I[:, :, 0].astype(float)
I_g = I[:, :, 1].astype(float)
I_b = I[:, :, 2].astype(float)
# 对每个通道进行对数变换
I_r_log = np.log(I_r + 1)
I_g_log = np.log(I_g + 1)
I_b_log = np.log(I_b + 1)
# 获取图像大小
m, n = I_r.shape
# 定义三个不同的高斯滤波核
sigma1 = 15
sigma2 = 80
sigma3 = 200
f1 = cv2.getGaussianKernel(m, sigma1)
f2 = cv2.getGaussianKernel(m, sigma2)
f3 = cv2.getGaussianKernel(m, sigma3)
f1 = f1.dot(f1.T)
f2 = f2.dot(f2.T)
f3 = f3.dot(f3.T)
# 对高斯滤波核进行FFT
efft1 = np.fft.fft2(f1)
efft2 = np.fft.fft2(f2)
efft3 = np.fft.fft2(f3)
# 对R,G,B通道进行FFT
Rfft1 = np.fft.fft2(I_r)
Gfft1 = np.fft.fft2(I_g)
Bfft1 = np.fft.fft2(I_b)
# 对每个通道进行频域滤波
D_r1 = np.fft.ifft2(Rfft1 * efft1)
D_g1 = np.fft.ifft2(Gfft1 * efft1)
D_b1 = np.fft.ifft2(Bfft1 * efft1)
D_r_log1 = np.log(D_r1 + 1)
D_g_log1 = np.log(D_g1 + 1)
D_b_log1 = np.log(D_b1 + 1)
R1 = I_r_log - D_r_log1
G1 = I_g_log - D_g_log1
B1 = I_b_log - D_b_log1
D_r2 = np.fft.ifft2(Rfft1 * efft2)
D_g2 = np.fft.ifft2(Gfft1 * efft2)
D_b2 = np.fft.ifft2(Bfft1 * efft2)
D_r_log2 = np.log(D_r2 + 1)
D_g_log2 = np.log(D_g2 + 1)
D_b_log2 = np.log(D_b2 + 1)
R2 = I_r_log - D_r_log2
G2 = I_g_log - D_g_log2
B2 = I_b_log - D_b_log2
D_r3 = np.fft.ifft2(Rfft1 * efft3)
D_g3 = np.fft.ifft2(Gfft1 * efft3)
D_b3 = np.fft.ifft2(Bfft1 * efft3)
D_r_log3 = np.log(D_r3 + 1)
D_g_log3 = np.log(D_g3 + 1)
D_b_log3 = np.log(D_b3 + 1)
R3 = I_r_log - D_r_log3
G3 = I_g_log - D_g_log3
B3 = I_b_log - D_b_log3
# 对每个通道