算法套路十二——回溯法之排列型回溯
- 该节是在第十节回溯法之子集型回溯的基础上进行描写,组合型回溯会在子集型回溯的基础上判断所选子集是否符合组合要求, 故请首先阅读第十节算法套路十——回溯法之子集型回溯
算法示例一:LeetCode46. 全排列
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
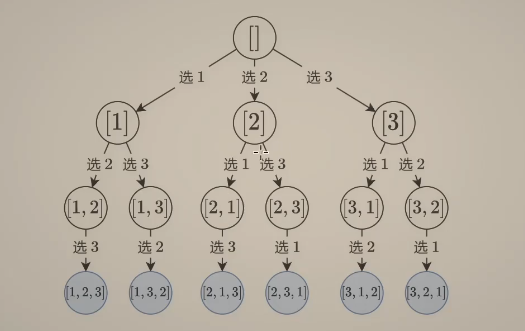
相比子集型回溯,排序型回溯的区别就是在选择相同子集时不会判断为重复,而是不同的排列,因此我们从答案的角度出发,考虑每次选哪一个数,且由于选择顺序不同排列也不同,故在递归时不用考虑要使后选的元素大于当前选的元素,那我们如何判断是否选择,可以使用on_path数组,来记录数组第i个元素是否被选择,且要在递归完成后回溯
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
n=len(nums)
ans=[]
path=[]
on_path=[False]*n
def dfs(i:int)-> None:
if i==n:
ans.append(path.copy())
return
for j in range(0,n):
if on_path[j]==False:
on_path[j]=True
path.append(nums[j])
dfs(i+1)
on_path[j]=False
path.pop()
dfs(0)
return ans
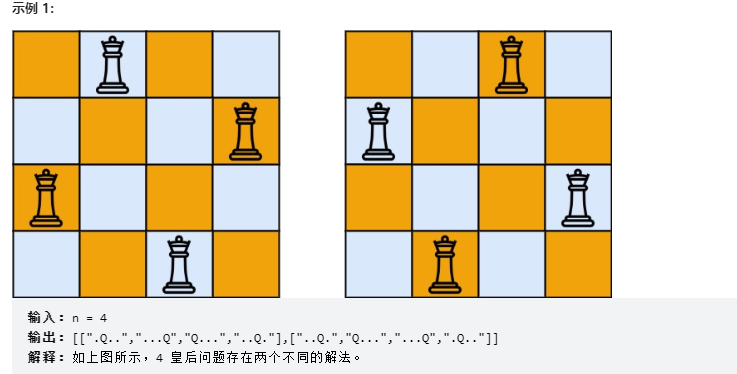
算法示例二:LeetCode51. N 皇后
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。
本题是一道回溯法的经典题,第一次做时可能感觉难,认为要求很多,但如果搞懂题目要求并能使用回溯就会发现很简单。题目即要求行i、列j、左对角线值即i-j,右对角线即i+j不能重复
- 用on_path记录当前列数是否已经被占据,
- 用inclined_left集合来记录i-j的值来判断左对角线是否已经被占据,i-j相同即在同一左对角线
- 用inclined_right集合来记录i-j的值来判断左对角线是否已经被占据,i+j相同即在同一右对角线
之后我们从答案的角度来对每一行应该选择哪一列来放皇后进行枚举,如果满足当前列数、左对角线、右对角线都没有占据,那么就记录、递归、回溯三步直接进行枚举
class Solution:
def solveNQueens(self, n: int) -> List[List[str]]:
path=[]
ans=[]
#列数
on_path=[False]*n
#左对角线,i-j相同即同一左对角线
inclined_left=set()
#右对角线,i+j相同即同一右对角线
inclined_right=set()
def dfs(i:int)->None:
if i==n:
ans.append(['.' * c + 'Q' + '.' * (n - 1 - c) for c in path])
return
#i行j列
for j in range(0,n):
if on_path[j]==False and i-j not in inclined_left and i+j not in inclined_right:
path.append(j)
on_path[j]=True
inclined_left.add(i-j)
inclined_right.add(j+i)
dfs(i+1)
path.pop()
on_path[j]=False
inclined_left.remove(i-j)
inclined_right.remove(j+i)
dfs(0)
return ans