前言:

之前我们初步的讲解了二叉树并且实现了堆这种特殊的二叉树，本次我们将实现链式二叉树的遍历(链式二叉树中非常重要的部分)，查找等功能。

附初识二叉树链接：http://t.csdn.cn/pMOia

一：二叉树的建立

(1)本文采用的二叉树表示方法

①每一个节点都是一个结构体。

②每一个节点除了存储数据，还存储了自己孩子节点的地址(结构体指针)。

③如果节点没有孩子就指向空。

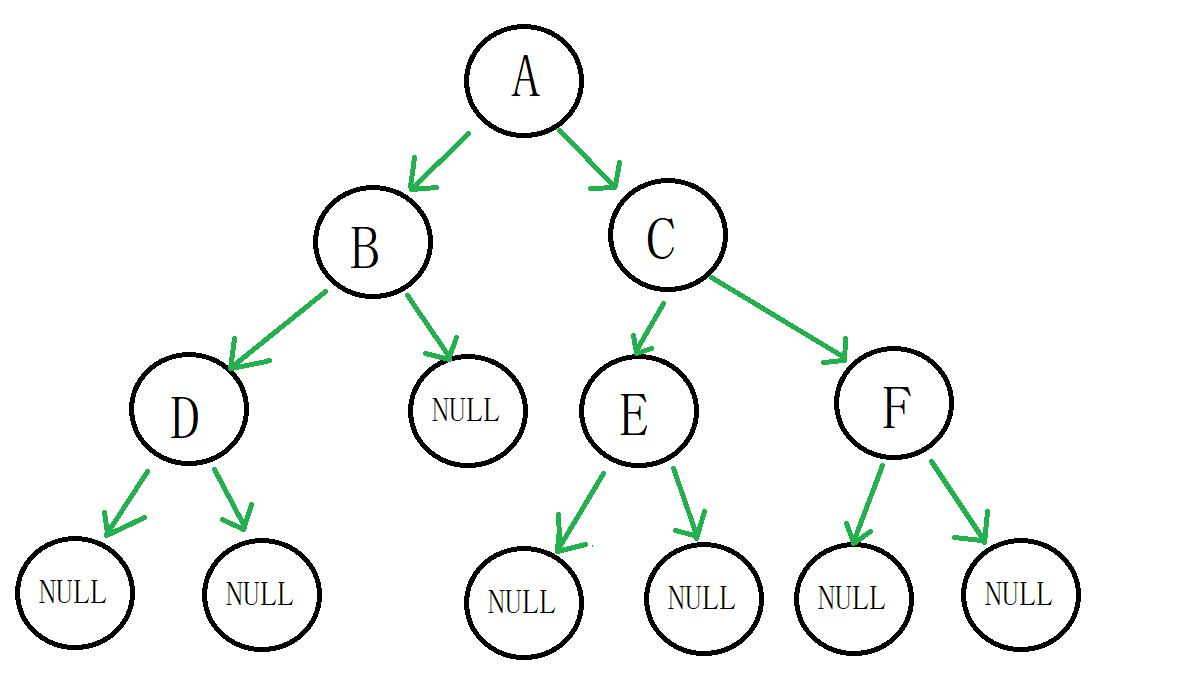
示意图：

代码：
typedef char BTDataType;

typedef struct BinaryTreeNode
{
	//存储左孩子的地址
	struct BinaryTreeNode* left;
	//存储右孩子的地址
	struct BinaryTreeNode* right;
	BTDataType data;
}BTNode;
(2)手动建立一颗二叉树

①调用malloc( )函数申请空间，插入数据。

②将节点依次链接。

③因为需要多次申请空间，插入数据，我们把这个部分封装成函数BuyNewNode( )。

代码：
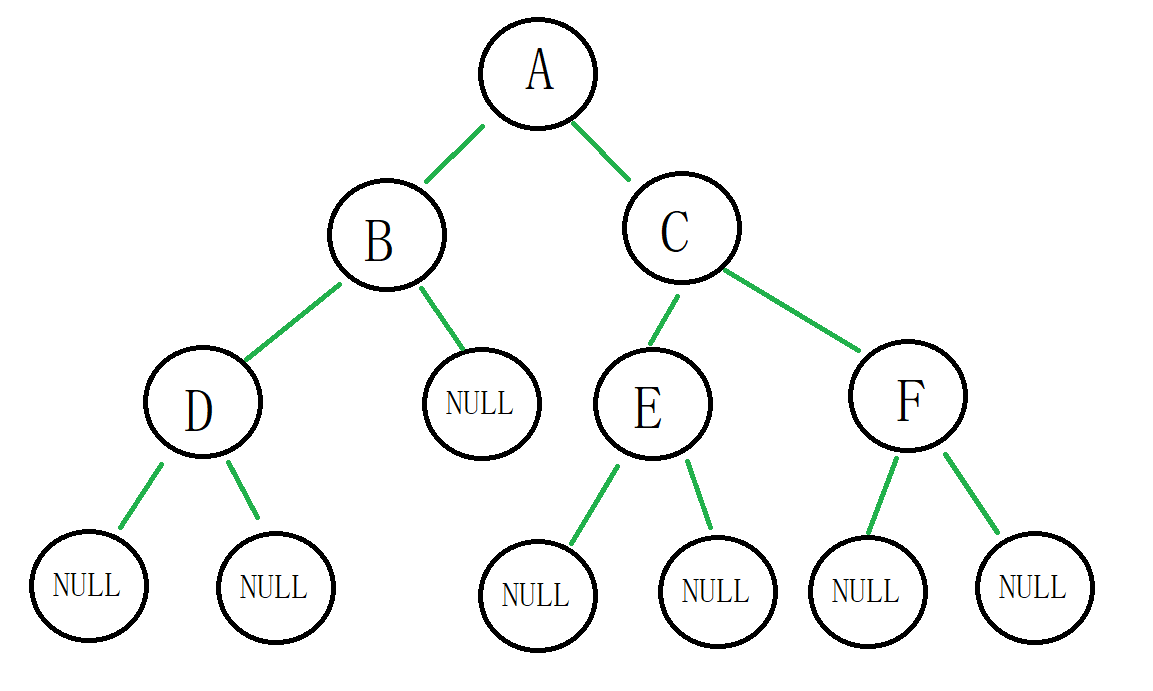
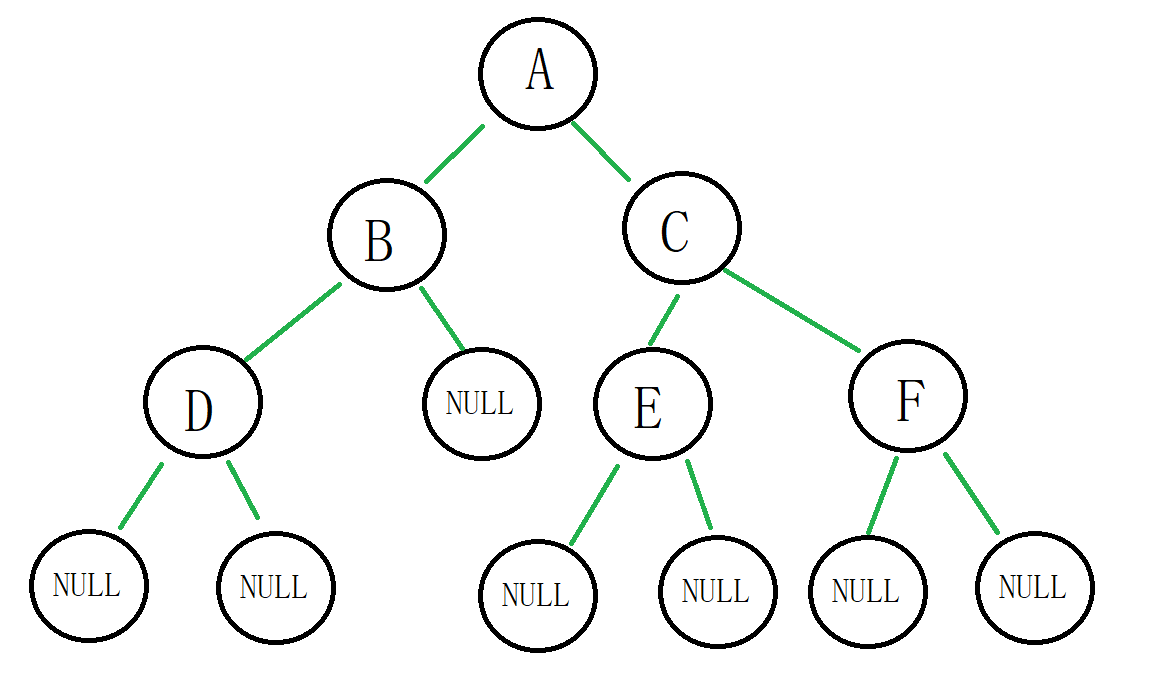
//申请新节点
BTNode* BuyNewNode(BTDataType x)
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	if (newnode == NULL)
	{
		printf("malloc error\n");
		exit(-1);
	}

	newnode->data = x;
	newnode->left = newnode->right = NULL;
	
	return newnode;
}


void test1()
{
    //手动建立一个二叉树
	BTNode* nodeA = BuyNewNode('A');
	BTNode* nodeB = BuyNewNode('B');
	BTNode* nodeC = BuyNewNode('C');
	nodeA->left = nodeB;
	nodeA->right = nodeC;
	BTNode* nodeD = BuyNewNode('D');
	BTNode* nodeE = BuyNewNode('E');
	BTNode* nodeF = BuyNewNode('F');
	nodeB->left = nodeD;
	nodeC->left = nodeE;
	nodeC->right = nodeF;
}
这个二叉树的图：

二：二叉树的遍历

(1)二叉树的三种遍历方式

1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右

子树之前。

2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中

（间）。

3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。

(2)分治思想

分治就是分而治之，大概意思就是将一个看似复杂的问题化成一个个简单的小问题，最后解决问题的思想，也是本文的核心。

好比一个学校要统计学生人数，可以让校长一个个去数，也可以让校长告诉年级主任，主任告诉班主任，班主任告诉宿舍长。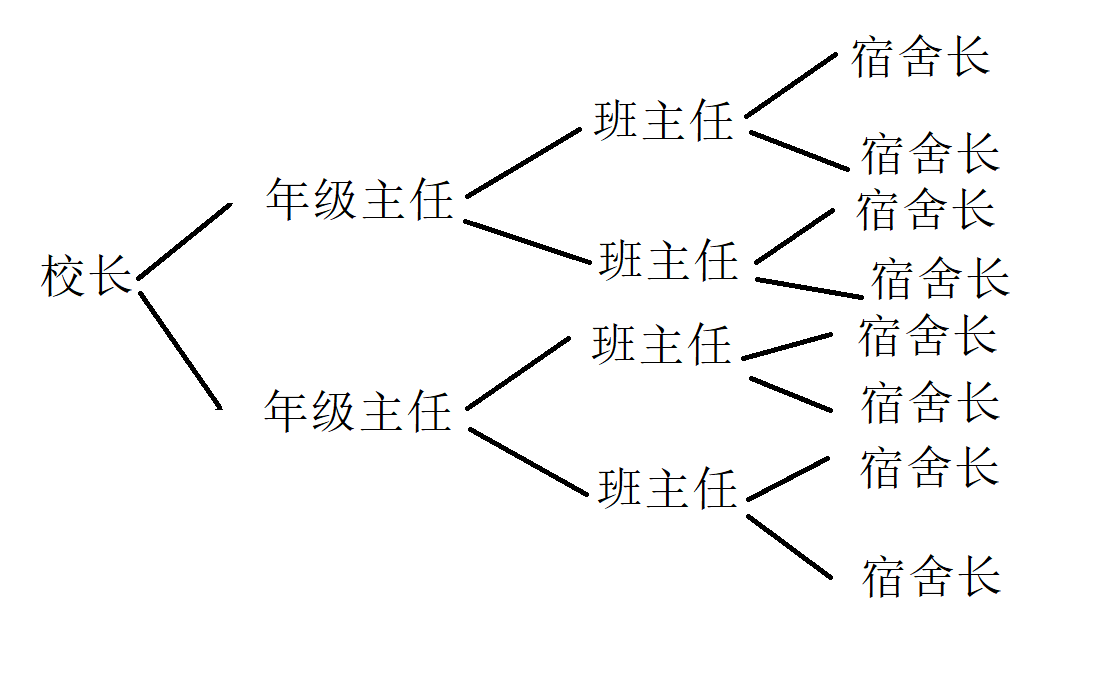

(3)前序遍历

① 我们看这颗二叉树，如果要进行前序遍历。

先打印A，然后遍历A左子树。

打印B，遍历B左子树。

打印D，遍历D左子树。

为空，遍历D右子树。

为空，B的左子树遍历结束，遍历B的右子树。

为空，A的左子树遍历结束，遍历A的右子树。

……………………

②我们不难发现，如果要前序遍历整棵树，

可以转化为先访问A后前序遍历A的左子树和右子树，

前序遍历A的左子树可以转化为先访问B后前序遍历B的左子树和右子树，

前序遍历B的右子树又可以转化为先访问D后前序遍历D的左子树和右子树，这样可以把一个较大的问题转化为一个个极小的问题。

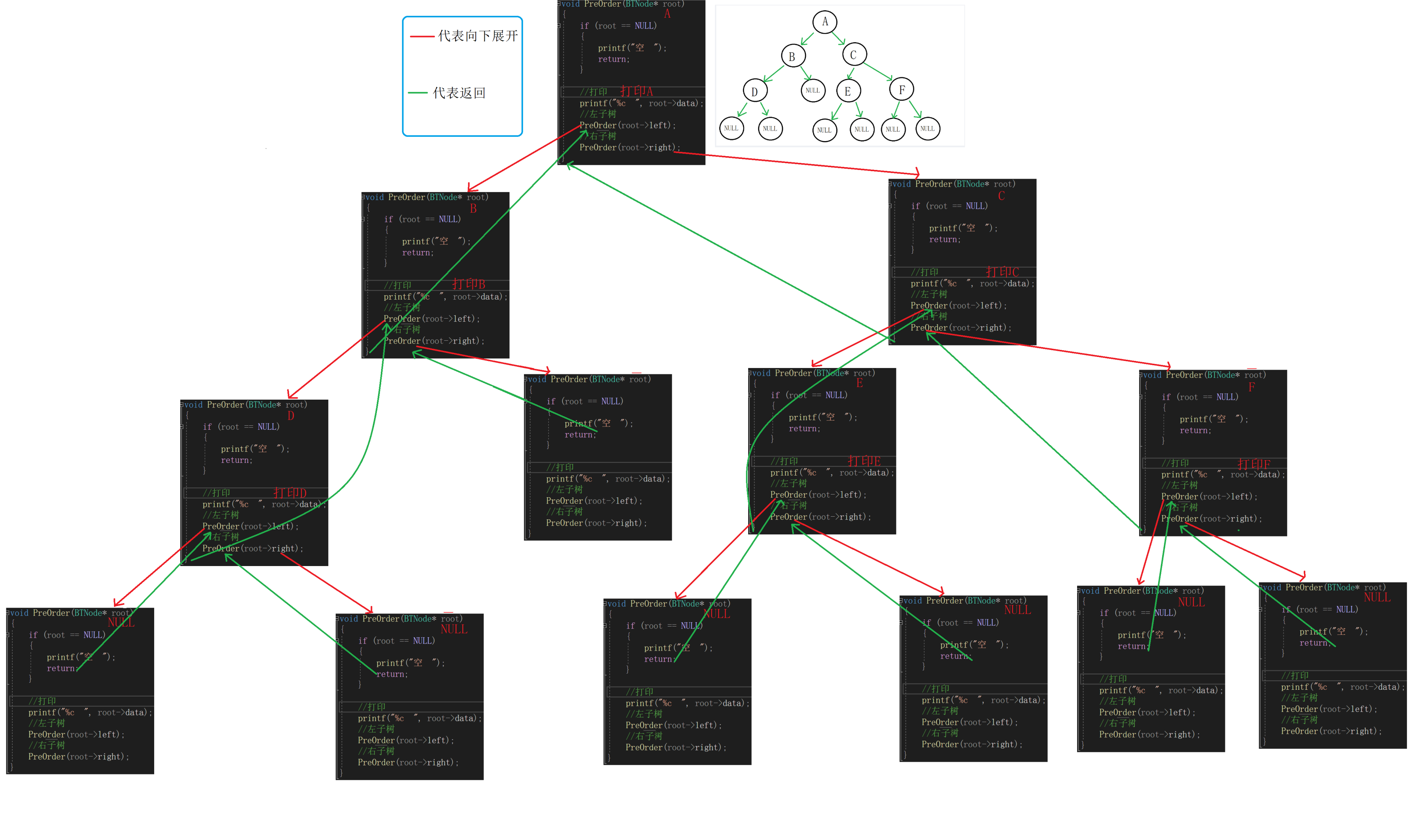
代码：
//前序遍历
void PreOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("空  ");
		return;
	}

	//打印
	printf("%c  ", root->data);
	//左子树
	PreOrder(root->left);
	//右子树
	PreOrder(root->right);
}
大家遇到这种递归不理解的话可以画一下递归展开图：

(4)中序遍历

①如果要对这颗二叉树进行中序遍历。

先遍历A左子树。

遍历B左子树。

遍历D左子树。

空，打印D，遍历D右子树。

空，打印B，遍历B右子树。

空，打印A，遍历A右子树。

………………

②中序遍历整颗树，

可以转化为中序遍历A的左子树后访问A，然后中序遍历右子树，

中序遍历A的左子树可以转化为中序遍历B的左子树后访问B，然后中序遍历右子树，

中序遍历B的右子树又可以转化为中序遍历D的左子树后访问D，然后中序遍历右子树，这样可以把一个较大的问题转化为一个个极小的问题。

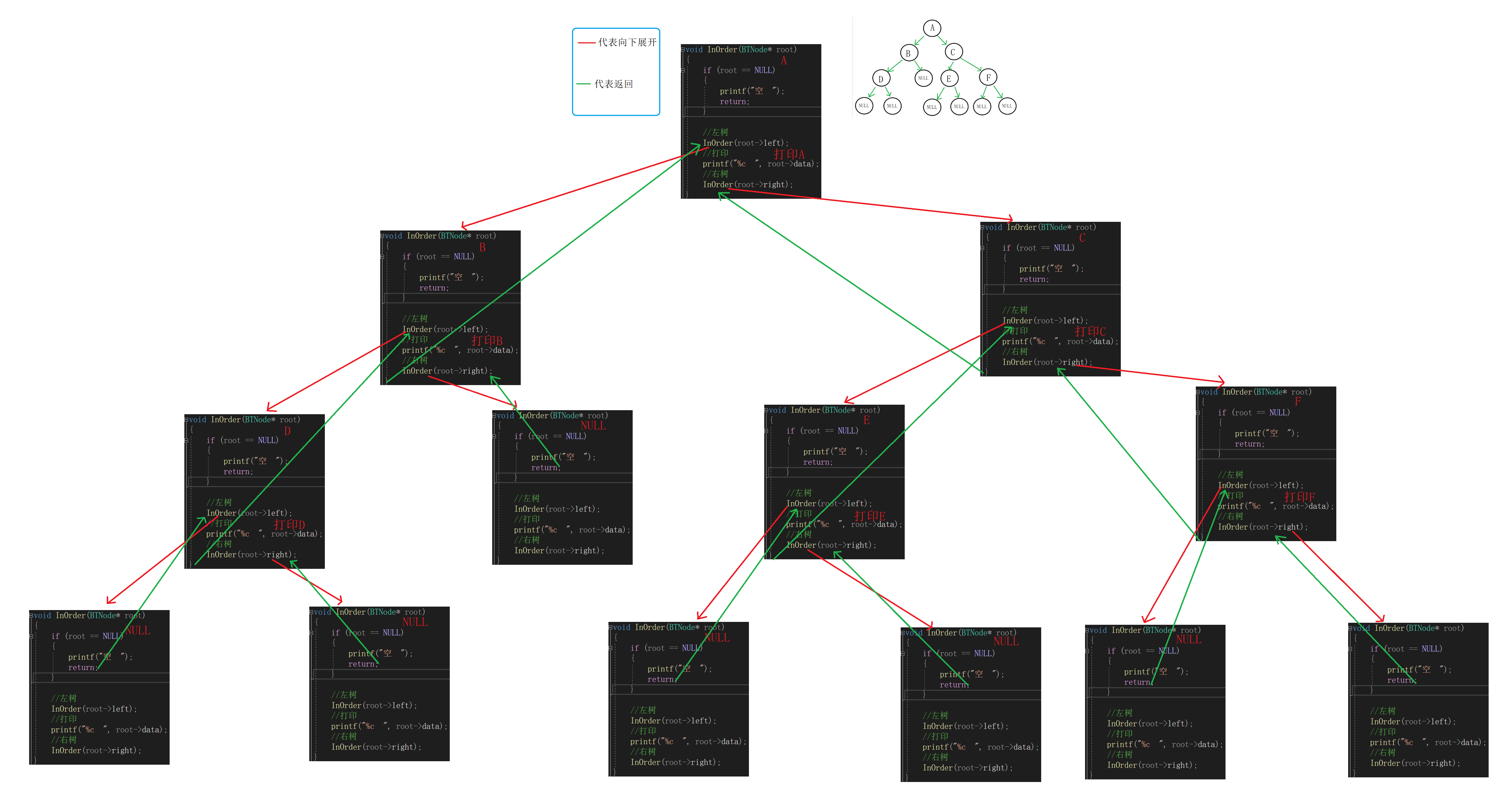
代码：
//中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("空  ");
		return;
	}

	//左树
	InOrder(root->left);
	//打印
	printf("%c  ", root->data);
	//右树
	InOrder(root->right);
}
递归展开图：

(5)后序遍历

①如果要对这颗二叉树进行后序遍历。

先遍历A左子树。

遍历B左子树。

遍历D左子树。

空，遍历D右子树。

空，打印D，遍历B右子树。

空，打印B，遍历A右子树。

……………………

②后序遍历整颗树，

可以转化为后序遍历A的左子树和右子树后访问A，

后序遍历A的左子树可以转化为后序遍历B的左子树和右子树后访问B，

后序遍历B的右子树又可以转化为后序遍历D的左子树和右子树后访问D，这样可以把一个较大的问题转化为一个个极小的问题。

代码：
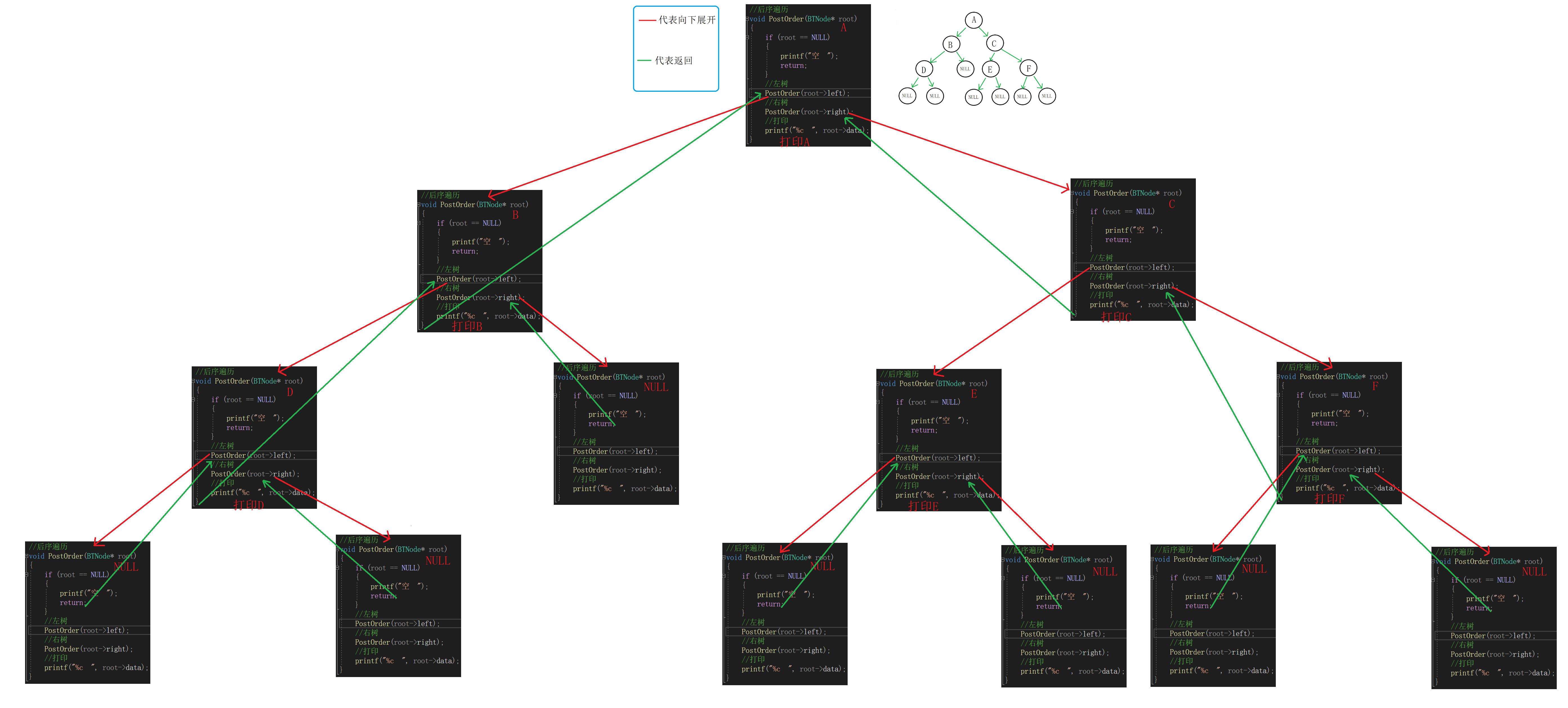
//后序遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("空  ");
		return;
	}
	//左树
	PostOrder(root->left);
	//右树
	PostOrder(root->right);
	//打印
	printf("%c  ", root->data);
}
递归展开图：

三：求二叉树的节点和高度(深度)

(1)求二叉树节点

①求二叉树的全部节点

思路：

①只有节点地址不为空就算一个节点。

②求整颗树节点，可以转化为A的左子树节点数加A的右子树节点数加1。

A的左子树节点数可以转化为B的左子树节点数加B的右子树节点数加1。

B的左子树节点数可以转化为D的左子树节点数加D的右子树节点数加1。

D的左右子树都是空，B的左子树节点数为1。

………………………………

代码：
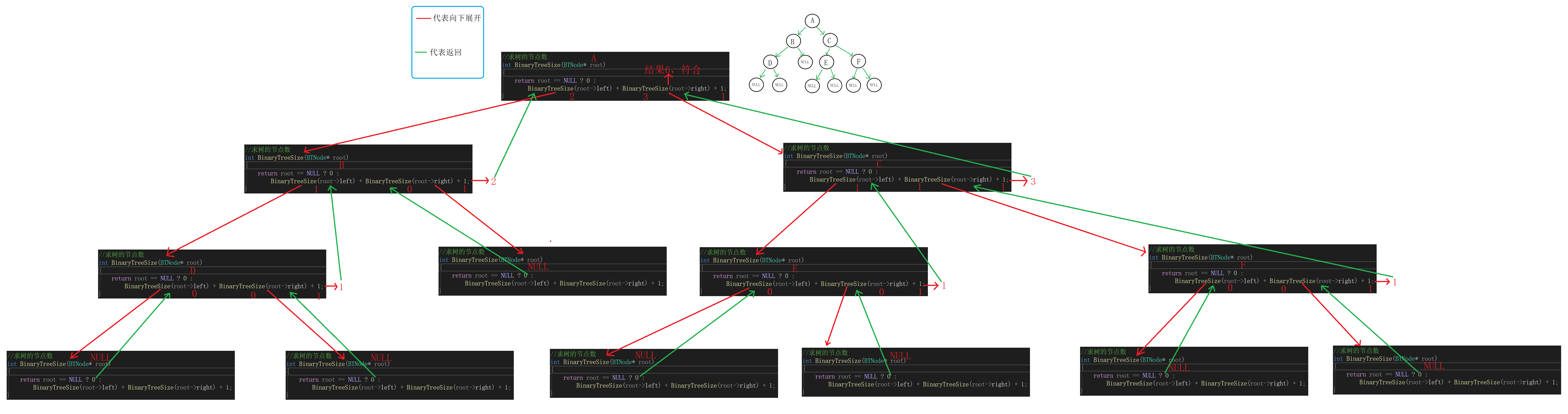
//求树的节点数
int BinaryTreeSize(BTNode* root)
{
	/*if (root == NULL)
	{
		return 0;
	}
	return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;*/
	//更加简洁的写法
	return root == NULL ? 0 :
		BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}
递归展开图：

②求二叉树的叶子节点

思路：

①左右孩子都为空的节点算作一个叶子节点。

②求整颗树的叶子节点，可以转化为求A的左子树叶子节点和A的右子树叶子节点。

求A的左子树叶子节点可以转化为求B的左子树叶子节点加B的右子树叶子节点。

D的左右孩子都为空，B的左子树叶子节点为1。

…………………………

代码：
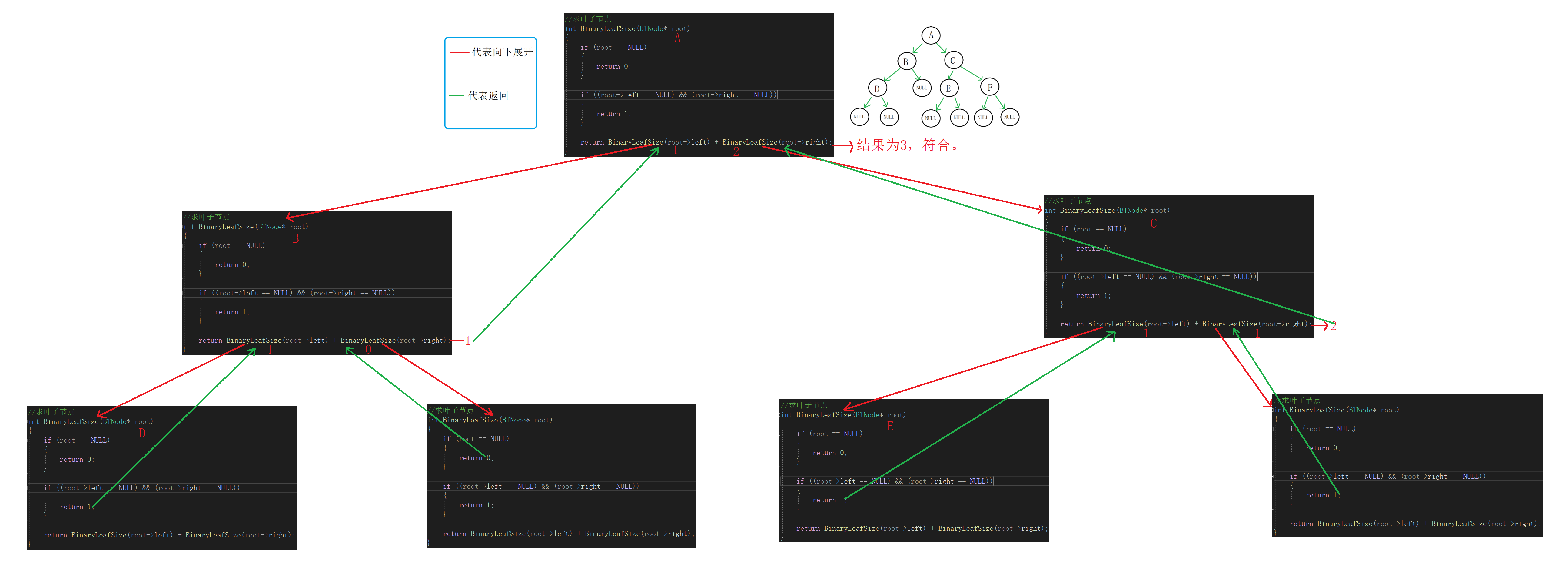
//求叶子节点
int BinaryLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}

	if ((root->left == NULL) && (root->right == NULL))
	{
		return 1;
	}

	return BinaryLeafSize(root->left) + BinaryLeafSize(root->right);
}
递归展开图：

③求二叉树第k层节点的个数

思路：

假设k为3。

①一颗树第一层节点数为1。

②空节点代表节点数为0。

③求整颗树第3层的节点数，可以转化为求A的左子树以及右子树的第2层节点数之和。

求A的左子树第2层节点数，可以转化为求B的左子树以及右子树的第1层节点数之和。

B左子树不为空，层数为1，节点数为1。

B的右子树为空，节点数为0。

………………………………

代码：
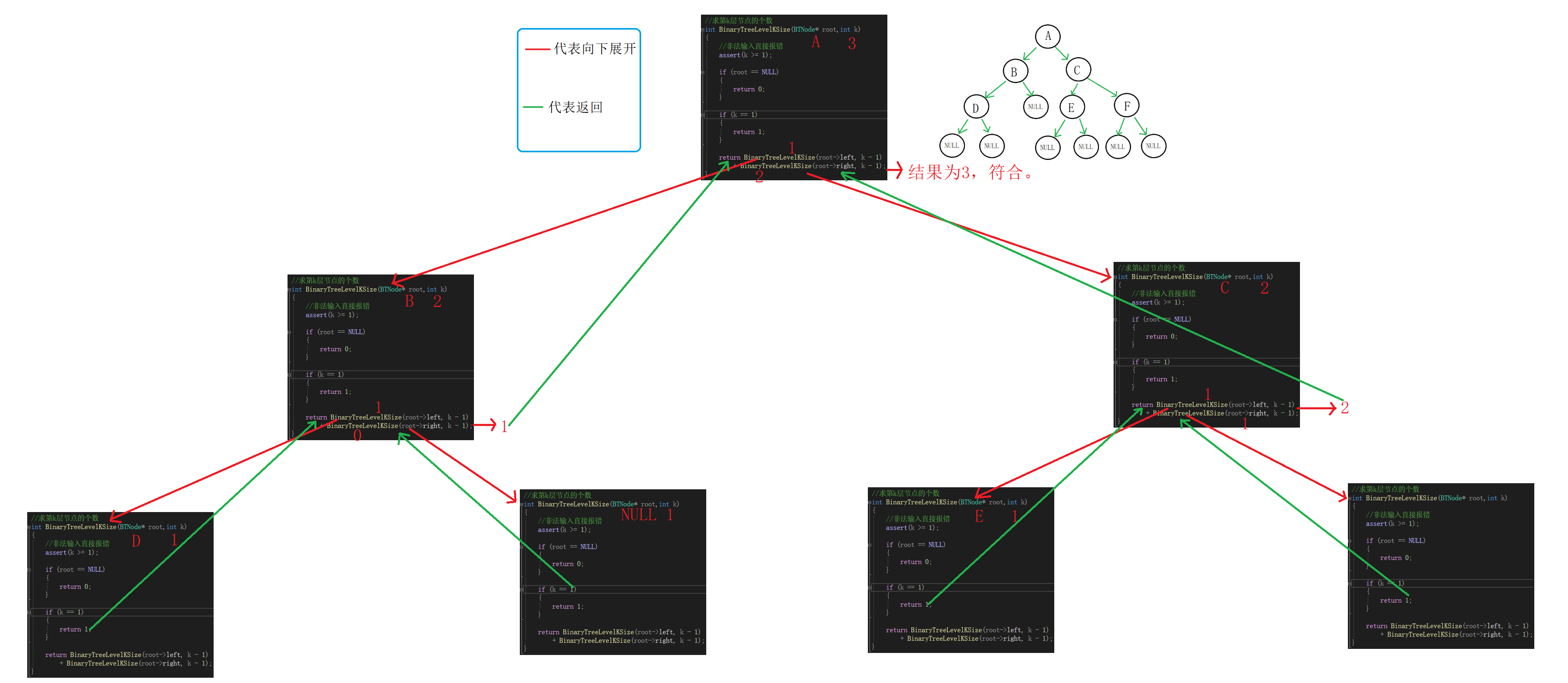
//求第k层节点的个数
int BinaryTreeLevelKSize(BTNode* root,int k)
{
	//非法输入直接报错
	assert(k >= 1);

	if (root == NULL)
	{
		return 0;
	}

	if (k == 1)
	{
		return 1;
	}

	return BinaryTreeLevelKSize(root->left, k - 1)
		+ BinaryTreeLevelKSize(root->right, k - 1);
}
递归展开图：

(2)求二叉树的高度(深度)

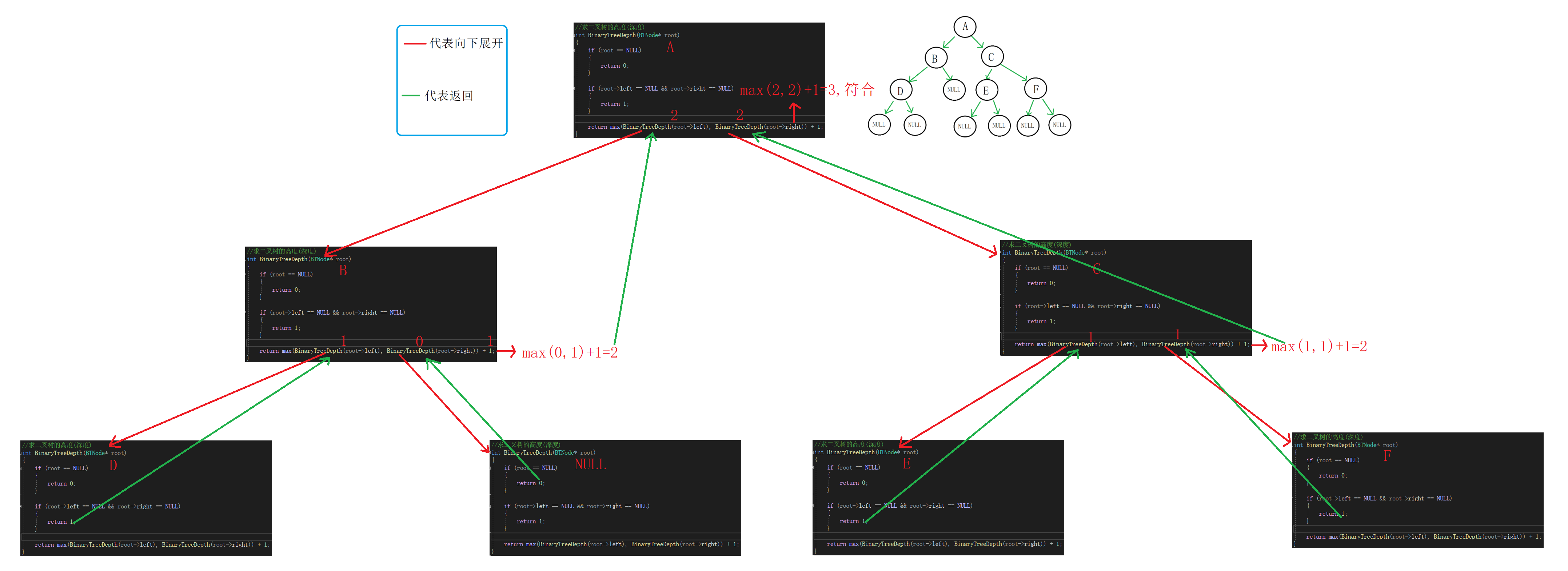
思路：

①空树高度为0。

②一颗树根节点左右孩子均为空，高度为1。

③一颗树最终的高度为左右子树中深度较大的一方加1。

④求整颗树的高度可以转化为A的左右子树中高度较大的一方加1。

求A的左子树高度可以转化为B的左右子树中高度较大的一方加1。

求B的左子树高度可以转化为D的左右子树中高度较大的一方加1。

D的左右孩子均为空，B的左子树高度为1。

B的右子树为空树，B的右子树高度为0。

取大的一方加1，A的左子树高度为2。

代码：
//求二叉树的高度(深度)
int BinaryTreeDepth(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}

	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}

	return max(BinaryTreeDepth(root->left), BinaryTreeDepth(root->right)) + 1;
}
递归展开图：

四：二叉树的查找

功能：输入要查找的数据x，返回节点的地址。

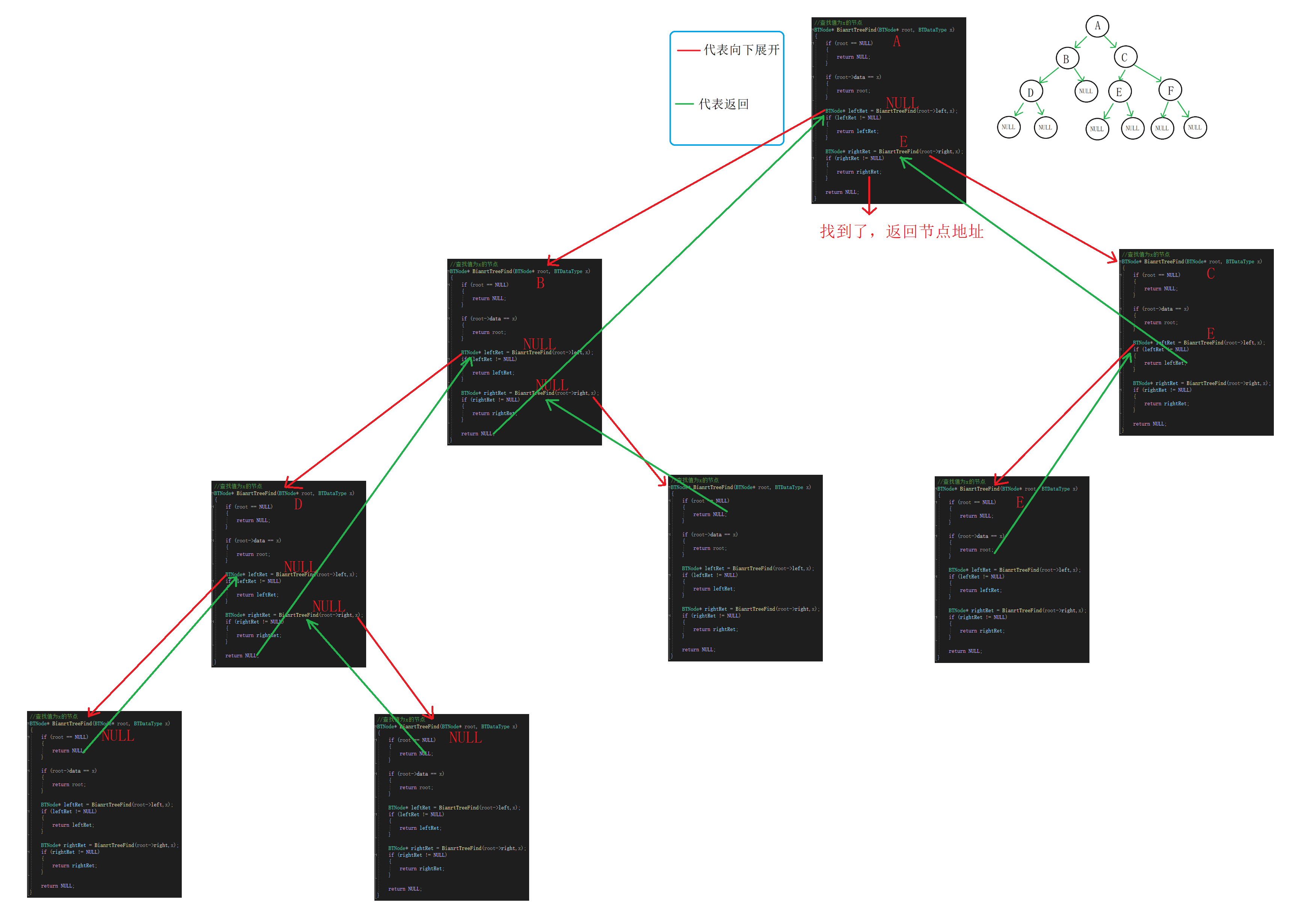
思路：

假设要查找E

①如果找到返回节点地址，没找到返回空。

②递归调用的时候要根据返回值来判断是否找到，

如果不为空代表找到了，不需要继续查找，返回节点地址。

③在整颗树查找E，先看根部是否为E，不是在A的左右子树中查找。

先看A的左子树根部是否为E，不是在B的左右子树中查找。

先看B的左子树根部是否为E，不是在D的左右子树中查找。

D的左右子树为空，返回空。

B的右子树为空，返回空。

A的左子树查找完毕，没找到，查找A的右子树。

先看A的右子树根部是否为E，不是在C的左右子树查找。

………………………………

代码：
//查找值为x的节点
BTNode* BianrtTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
	{
		return NULL;
	}

	if (root->data == x)
	{
		return root;
	}

	BTNode* leftRet = BianrtTreeFind(root->left,x);
	if (leftRet != NULL)
	{
		return leftRet;
	}

	BTNode* rightRet = BianrtTreeFind(root->right,x);
	if (rightRet != NULL)
	{
		return rightRet;
	}

	return NULL;
}
递归展开图(查找E)：