基于Powell共轭方向法的UWB室内定位构型优化算法
阚昊宇
摘要: UWB室内定位系统的服务性能及定位精度很大程度上受UWB基站构型影响,而GDOP是衡量系统定位服务性能的重要指标。目前关于UWB室内定位基站构型的讨论主要集中于最小化限定基站数目下GDOP在自由空间的理论分布,在实际应用中需要有便捷可行的算法来指导不同限制的室内环境下的基站布设状况。本文提出基于Powell共轭方向线性搜索优化算法,可以基于指定区域的GDOP值最小化原则对任意数量基站的构型进行优化,并给出可行的基站位置坐标,从而提高UWB室内定位系统在指定区域的整体精度期望。
关键词: 室内定位;UWB;GDOP
Optimization Algorithm of UWB Indoor Positioning Configuration Based on
Powell Conjugate Direction Method
Absrtact: The service performance and positioning accuracy of the
UWB indoor positioning system are largely affected by the configuration
of the UWB base station, and GDOP is an important indicator to measure
the positioning performance of a positioning system. At present, the
discussion on the configuration of UWB indoor positioning base stations
mainly focuses on the theoretical distribution of GDOP in free space
under the minimum number of limited base stations. In practical
applications, a convenient and feasible algorithm is required to guide
the layout of base stations under different indoor environments. In this
paper, we propose a Powell conjugate direction based linear search
optimization algorithm, which can optimize the configuration of any
number of base stations based on the principle of minimizing the GDOP
value in the designated area, and produce feasible coordinates for the
base stations, so as to improve the overall accuracy expectation of the
UWB indoor positioning system in the designated area.
Key words: indoor positioning; UWB; GDOP
1 研究背景
空间位置信息与人类生产生活密切相关,社会经济的发展使得室内定位的应用场景越来越多,室内定位技术需求不断增长。相比室外环境,室内的环境更为复杂,因此出现了多种室内定位技术手段。其中,超宽带(Ultra
Wideband,UWB)技术利用功率谱密度极低、脉冲宽度极窄的脉冲携带信息,具有较高的时间分辨率和更大的带宽,受到非视距(Non-Line-of-Sight,NLOS)误差和多路径效应的影响较小,能达到比WLAN、蓝牙、RFID等技术更高的定位精度[1]。
在UWB定位过程中,一般通过测量或匹配方式进行定位,常用的测量定位方式有基于到达时间(Time of Arrival, TOA)[2]、基于到达时间差(Time Difference of Arrival, TDOA)[3],基于到达角度(Angle of Arrival, AOA)[4]等方式,静态定位精度一般可以达到dm级;匹配定位方式一般基于RSSI接收信号强度指数(Received Signal Strength Indication,RSSI)[5],但是对于UWB,基于RSSI方法的定位精度相对测量定位方式一般较差,仅能达到m级[6]。因此,本文主要讨论的是测量定位方式的定位性能及改进方法。
对于采用测量定位方式的测量系统,其定位参数估计的精确度与观测数据质量、空间几何构型有关。观测数据质量与信号接收与发送设备、环境相关,而模型空间几何构型对定位性能的影响一般通过几何精度因子(Geomatric
Dilution of Precision,GDOP)指标衡量[7]。GDOP起源于美国的Loran
C导航系统,后广泛应用于描述卫星定位的空间几何构型对单点定位估计结果的影响。作为一种测量误差的放大比例因子,GDOP值越小,系统定位精度越高。因此,可基于GDOP最小化准则进行定位构型的优化设计。在最小化单个点的GDOP条件下,可以给出多种理论最优的定位构型解[8],然而,在室内复杂环境下,基站可布设的位置受到限制,而且,用户往往关注在某一个区域而不是单个点上的定位精度。如何结合建筑物空间结构进行合理布设基站,并在基站个数和定位精度之间平衡,是研究定位构型优化的重点[9]。
综上,结合建筑物空间结构进行定位构型优化可以被表达为一种有界约束最小化问题。有界约束最小化问题。Powell共轭方向法是常用的有界约束最小化方法[10]。它沿着搜索方向组的每个向量,按顺序执行线性寻优,之后在主循环迭代时更新参数值。如果提供了边界,并且初始猜测值在边界内,那么整个最小化过程中的每个函数求值都将在边界内。Powell共轭方向法不要求函数可微的,也不需要求导数,因此适合进行室内定位构型GDOP优化。
2 方法
2.1 Powell共轭方向法
Powell方法是一种常用的无导数最优化方法,对于目标函数 f : R n → R f:\mathbb{R}^{n}\mathbb{\rightarrow R} f:Rn→R的最小化问题,原始的Powell算法如下[11]:
- 设参数初值
X
0
∈
R
n
X_{0} \in \mathbb{R}^{n}
X0∈Rn,线性无关的初始搜索方向组
ξ
i
(
i
=
1
,
⋯
,
n
)
\xi_{i}(i = 1,\cdots,n)
ξi(i=1,⋯,n)
,迭代次数 k k k=0,给定允许误差 ε \varepsilon ε; - 令 X k , 0 = X k X_{k,0} = X_{k} Xk,0=Xk,按次序 i = 1 , ⋯ , n i = 1,\cdots,n i=1,⋯,n沿着方向 ξ i \xi_{i} ξi分别做一维寻优,得到
f ( X k , i − 1 + α i ξ i ) = min α f ( X k , i − 1 + α ξ i ) f\left( X_{k,i - 1} + \alpha_{i}\xi_{i} \right) = \min_{\alpha}f\left( X_{k,i - 1} + \alpha\xi_{i} \right) f(Xk,i−1+αiξi)=αminf(Xk,i−1+αξi)
- 令 X k , i = X k , i − 1 + α i ξ i X_{k,i} = X_{k,i - 1} + \alpha_{i}\xi_{i} Xk,i=Xk,i−1+αiξi, ξ n + 1 = X k , n − X k , 0 = ∑ i = 1 n α i ξ i \xi_{n + 1} = X_{k,n} - X_{k,0} = \sum_{i = 1}^{n}\alpha_{i}\xi_{i} ξn+1=Xk,n−Xk,0=∑i=1nαiξi,并沿着 ξ n + 1 \xi_{n + 1} ξn+1做一维寻优,得到
f ( X k , n + α n + 1 ξ n + 1 ) = min α f ( X k , n + α ξ n + 1 ) f\left( X_{k,n} + \alpha_{n + 1}\xi_{n + 1} \right) = \min_{\alpha}f\left( X_{k,n} + \alpha\xi_{n + 1} \right) f(Xk,n+αn+1ξn+1)=αminf(Xk,n+αξn+1)
- 令 X k + 1 = X k , n + α n + 1 ξ n + 1 X_{k + 1} = X_{k,n} + \alpha_{n + 1}\xi_{n + 1} Xk+1=Xk,n+αn+1ξn+1,若满足
∣ X k + 1 − X k ∣ ≤ ε \left| X_{k + 1} - X_{k} \right| \leq \varepsilon ∣Xk+1−Xk∣≤ε
- 则认为算法收敛, X k + 1 X_{k + 1} Xk+1为问题的最优解,否则迭代次数 k = k + 1 k = k + 1 k=k+1,返回第3步。
原始Powell算法可用于求解一般无约束优化问题,但在原始的Powell算法中,当某一循环方向组中的矢量系出现线性相关的情况(退化,病态)时,搜索过程将局限在降维的空间进行,致使计算不能收敛而失败。为了避免原始Powell算法缺陷,Powell提出了相应的修正算法[10],主要区别在于在构成第 k + 1 k + 1 k+1次循环的搜索方向组时,通过计算前一轮迭代法中函数值下降最多的方向 m m m及其下降量 Δ m \Delta m Δm来检验是否需要调整搜索方向。如果给定了参数限制条件,则仅会在满足参数限制条件的范围内进行优化。
2.2 GDOP计算方法
GDOP关于是否考虑钟差分为两种计算方法[7]:第一类GDOP不考虑钟差,也称PDOP[12];第二类GDOP考虑钟差。
对于一个由 n n n个已知坐标点组成的测距类型定位系统,有如下观测方程[13]:
l i = d i ( x ) + Δ + ε i i = 1 , . . . , n l_{i} = d_{i}\left( \mathbf{x} \right) + \Delta + \varepsilon_{i}\quad i = 1,...,n li=di(x)+Δ+εii=1,...,n
其中, d i ( x ) d_{i}\left( \mathbf{x} \right) di(x)为待测点 x = [ x , y , z ] ∈ R 3 \mathbf{x} = \lbrack x,y,z\rbrack \in \mathbb{R}^{3} x=[x,y,z]∈R3相对于已知点 c i = [ x i , y i , z i ] \mathbf{c}_{i} = \left\lbrack x_{i},y_{i},z_{i} \right\rbrack ci=[xi,yi,zi]的欧氏距离, Δ \Delta Δ为待测点接收机钟差, ε i \varepsilon_{i} εi为测距噪声。
将位置参数与钟差作为待估参数合并,进行观测方程线性化后,系数矩阵
A = [ a x 1 a y 1 a z 1 1 a x 2 a y 2 a z 2 1 ⋮ ⋮ ⋮ ⋮ a x n a y n a z n 1 ] \mathbf{A} = \begin{bmatrix} a_{x}^{1} & a_{y}^{1} & a_{z}^{1} & 1 \\ a_{x}^{2} & a_{y}^{2} & a_{z}^{2} & 1 \\ \vdots & \vdots & \vdots & \vdots \\ a_{x}^{n} & a_{y}^{n} & a_{z}^{n} & 1 \\ \end{bmatrix} A= ax1ax2⋮axnay1ay2⋮aynaz1az2⋮azn11⋮1
其中, a { x , y , z } i a_{\{ x,y,z\}}^{i} a{x,y,z}i为该方向上的方向余弦向量,令待估参数的法方程逆阵 ( A T A ) − 1 \left( A^{T}A \right)^{- 1} (ATA)−1为:
( A T A ) − 1 = [ D 11 D 12 D 13 D 14 D 21 D 22 D 23 D 24 D 31 D 32 D 33 D 34 D 41 D 42 D 43 D 44 ] \left( \mathbf{A}^{T}\mathbf{A} \right)^{- 1} = \begin{bmatrix} D_{11} & D_{12} & D_{13} & D_{14} \\ D_{21} & D_{22} & D_{23} & D_{24} \\ D_{31} & D_{32} & D_{33} & D_{34} \\ D_{41} & D_{42} & D_{43} & D_{44} \\ \end{bmatrix} (ATA)−1= D11D21D31D41D12D22D32D42D13D23D33D43D14D24D34D44
第一类GDOP表达式为:
G D O P ′ ( c , x ) = P D O P = D 11 + D 22 + D 33 GDOP^{'}\left( \mathbf{c},\mathbf{x} \right) = PDOP = \sqrt{D_{11} + D_{22} + D_{33}} GDOP′(c,x)=PDOP=D11+D22+D33
第二类GDOP表达式为:
G D O P ′ ′ ( c , x ) = D 11 + D 22 + D 33 + D 44 GDOP^{''}\left( \mathbf{c},\mathbf{x} \right) = \sqrt{D_{11} + D_{22} + D_{33} + D_{44}} GDOP′′(c,x)=D11+D22+D33+D44
由于目前大部分UWB测量定位系统采用双向测距(Two-Way
Ranging,TWR)方法消除接收机钟差[9],因此本文主要考虑第一类GDOP。
2.3 本文算法具体步骤
首先,确定允许的基站布设空间 S S S和定位关注区域 F F F,一般由三维空间中的若干组不等式表达。例如,对于一个长宽高分别为 a , b , c a,b,c a,b,c的方形大厅,定位关注区域为其中高为 h h h的整个平面,可以表示为如下条件:
S : { 0 < x < a 0 < y < b 0 < z < c S:\quad\left\{ \begin{matrix} 0 < x < a \\ 0 < y < b \\ 0 < z < c \\ \end{matrix} \right.\ S:⎩ ⎨ ⎧0<x<a0<y<b0<z<c
F : { 0 < x < a 0 < y < b z = h F:\quad\left\{ \begin{matrix} 0 < x < a \\ 0 < y < b \\ z = h \\ \end{matrix} \right.\ F:⎩ ⎨ ⎧0<x<a0<y<bz=h
然后,对 n n n个基站坐标 { c i } , c i ∈ R 3 , ( i = 1 , ⋯ , n ) \{\mathbf{c}_{i}\},\mathbf{c}_{i} \in \mathbb{R}^{\mathbb{3}},(i = 1,\cdots,n) {ci},ci∈R3,(i=1,⋯,n)进行随机初始化,保证坐标落入 S S S内,且不具有共线性。接下来,要使得每个基站在定位关注区域 F F F中第一类GDOP的分布整体最小,即让如下目标优化函数最小
f ( c ) = ∑ i ∭ F G D O P ′ ( c i , x , y , z ) d V f\left( \mathbf{c} \right) = \sum_{i}^{}{\iiint_{F}^{}{GDOP'(\mathbf{c}_{i},x,y,z)\mathbb{d}V}} f(c)=i∑∭FGDOP′(ci,x,y,z)dV
由于该函数计算复杂,需要进行简化,简化方法如下:在定位关注区域内进行采样,例如以均匀间隔进行采样,得到采样点集合 { x j } , x j ∈ R 3 \{\mathbf{x}_{j}\},\mathbf{x}_{j} \in \mathbb{R}^{\mathbb{3}} {xj},xj∈R3。
最后,采用Powell方法对新的目标优化函数
f ( c , x ) = ∑ i ∑ j G D O P ′ ( c i , x j ) f\left( \mathbf{c},\mathbf{x} \right) = \sum_{i}^{}{\sum_{j}^{}{GDOP^{'}\left( \mathbf{c}_{i},\mathbf{x}_{j} \right)}} f(c,x)=i∑j∑GDOP′(ci,xj)
在满足
S
S
S的条件下进行寻优,当迭代前后所有的基站坐标
{
x
j
}
\{\mathbf{x}_{j}\}
{xj}的改变量的范数收敛时,认为优化完成,此时的基站坐标即为当前条件下一个可能的最优解。由于该算法受到初始化值的影响,所以可能需要多次随机初始化基站坐标,以达到最优解。整体流程图如下图
1所示。
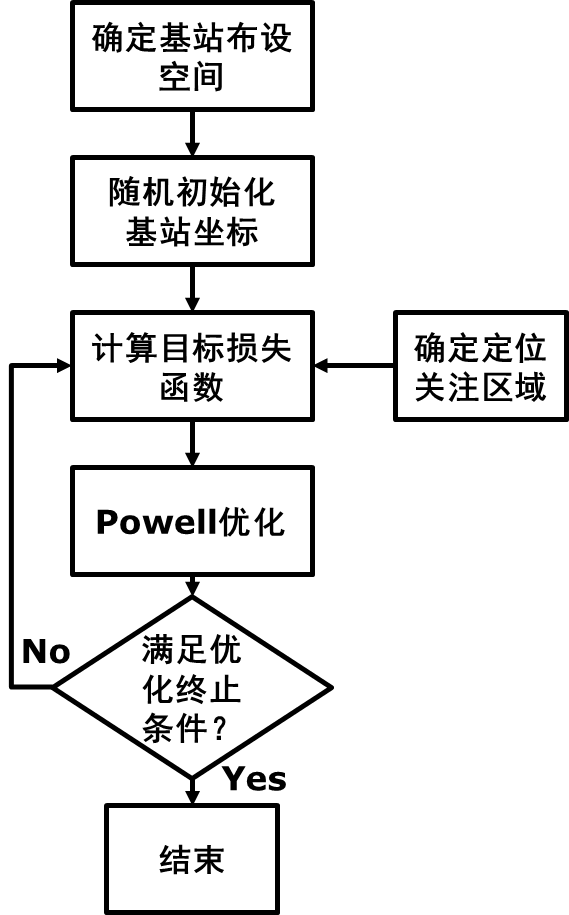
图 1 本文算法流程图
3 仿真场景
以下分别设置三种常见的室内定位情景,如下表 1所示:
表 1 仿真场景设置
| 编号 | 场景 | 定位关注区域 | 基站可布设区域 | 基站数量 |
|---|---|---|---|---|
| 1 | 方形大厅 | 全部 | 方形大厅内任意点 | 4/5/8 |
| 2 | 方形大厅内的过道 | 部分 | 方形大厅内任意点 | 4/5/8 |
| 3 | 狭长隧道 | 全部 | 狭长隧道内任意点 | 4/5/8 |
从第一种最简单的场景开始,第二种和第三种分别代表了定位关注区域的改变与基站布设空间限制的改变。此外,增加了基站数量的变化这一维度,由于成本限制,一般情况下一个定位单元(如一个房间)仅会布置4个基站,本文算法也可提供基站成本增加与定位精度提升之间关系的参考。
3.1 方形大厅
在一个长宽高为20 m×20 m×4
m的正方形大厅内,分别布设4/5/8个基站,基站可以布设在该大厅内的任意位置,定位关注区域平面高度约束为1.7
m(采样点在图中表示为蓝色线网)。长宽高在图中分别对应ENZ方向,下同。
由本文算法优化得到基站坐标优化结果如下图
2(a)( c)(e)所示,基站为蓝色三角点。定位关注区域平面的PDOP值如下图
2(b)(d)(f)所示。显然,当基站数量增加时,平均PDOP值持续下降。


图 2 场景1方形大厅的4/5/8基站优化结果
3.2 方形大厅里的通道
在一个长宽高为20 m×20 m×4
m的正方形大厅内,分别布设4/5/8个基站,基站可以布设在该大厅内的任意位置,定位关注区域平面高度约束为1.7
m。但是,假设定位用户只会经过西侧一条4 m宽的通道(采样点在图
3中表示为蓝色线网),也即,定位精度的关注区域仅限于该通道。由本文算法优化得到基站坐标优化结果如下图
3(a)©(e)所示,基站为蓝色三角点。定位关注区域平面的PDOP值如下图
3(b)(d)(f)所示,其中,定位关注区域(即过道)用红色框标注。可见,当基站数量增加时,优化算法能使得定位关注区域的平均PDOP值持续下降。本文算法计算得出的基站位置尽量保证定位关注区域的PDOP最小,并且,相较于3.1节中的结果,4/5/8基站定位关注区域的PDOP分别下降了24.0%、19.0%和13.3%,说明在基站数量较少时,通过限定用户活动范围、划定定位关注区域获得的定位精度提升更多。


图 3 场景2方形大厅里的通道的4/5/8基站优化结果
3.3 狭长隧道
在一个长宽高为100 m×3 m×3
m的狭长隧道内,分别布设4/5/8个基站,基站可以布设在隧道内的任意位置,定位关注区域平面高度约束为1.7
m。由本文算法优化得到基站坐标优化结果如下图
4(a)©(e)所示,基站为蓝色三角点。定位关注区域平面的PDOP值如下图
4(b)(d)(f)所示,其中,定位关注区域(即隧道)用红色框标注。需要注意的是,下图
4(a)©(e)中长方向(E方向)量级远大于其他两个方向。由图
4可见,本文算法计算得出的基站位置尽量保证定位关注区域的PDOP最小。但是由于隧道过于狭长,4基站三维定位的精度因子衰减迅速,普通UWB定位系统的测距噪声由dm级被放大到数十m的级别,不足以满足三维定位需求。说明在室内定位环境苛刻时,需要调整基站数量选取策略或降低定位维度需求,以达到合理的定位效果。
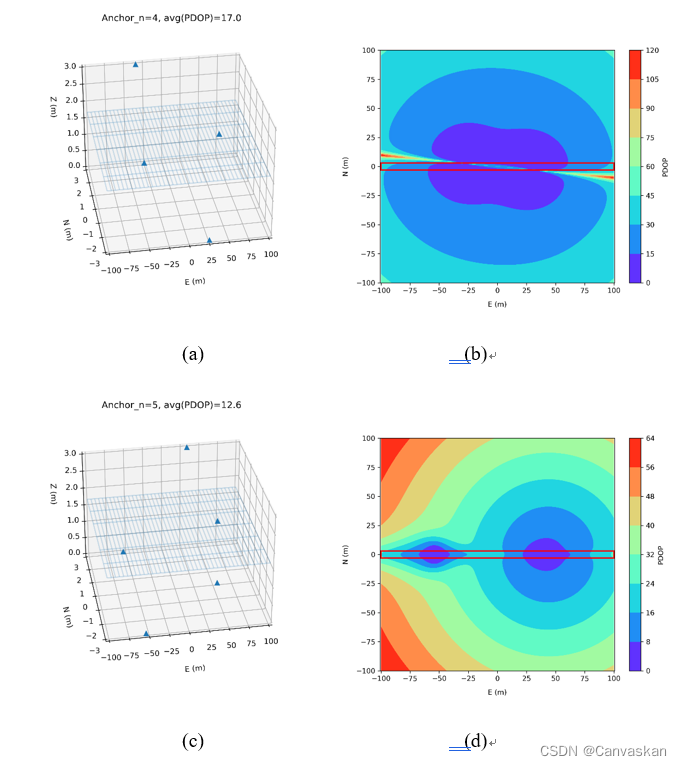
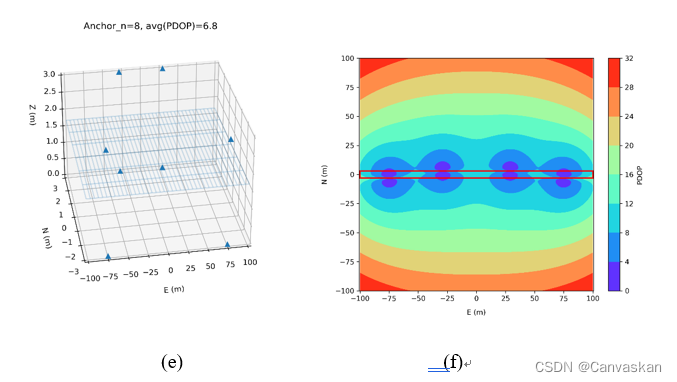
图 4 场景3狭长隧道的4/5/8基站优化结果
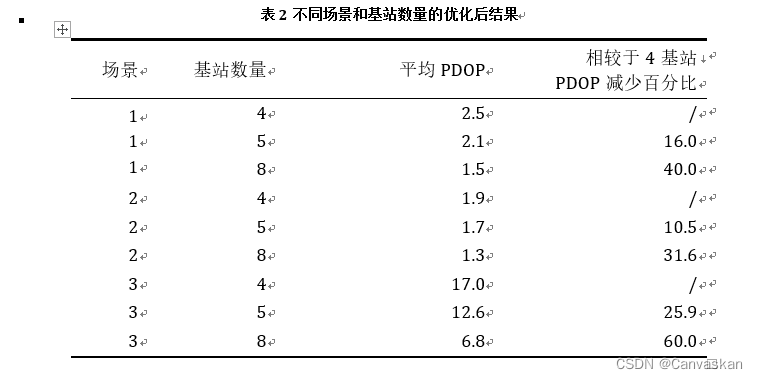
不同场景和基站数量的优化后的平均PDOP如下表所示,同时统计了增加基站相对于4基站标准情况的改进情况,一并列于表中。
表 2不同场景和基站数量的优化后结果
4 结论
本文基于指定区域的GDOP值最小化原则提供一种便捷可行的方法来指导不同限制的室内环境下的UWB基站布设状况,通过三个仿真场景的计算,验证了本文算法的有效性,同时得出了以下初步结论:
-
当基站数量增加时,本文优化算法能使得定位关注区域的平均GDOP值持续下降,计算得出的基站位置尽量保证定位关注区域的GDOP最小。
-
在基站数量较少时,通过限定用户活动范围、划定定位关注区域获得的定位精度提升效果更显著。
-
室内定位环境苛刻时,需要调整基站数量选取策略或降低定位维度需求,以达到合理的定位效果。
本文还没有考虑墙壁等遮挡物对信号传播路径造成的NLOS、多路径等影响,算法也存在结果与初始化相关、不一定收敛至最优解等问题,仍需要进一步改进。(后来发现L-BFGS-B方法代替Powell方法似乎更容易得到更优的解,初始化次数更少,具体原因有待分析)。
参考文献
[1] Mazhar F, Khan M G, Sällberg B. Precise Indoor Positioning Using
UWB: A Review of Methods, Algorithms and Implementations [J]. Wireless
Personal Communications, 2017, 97 (3): 4467-91.
[2] Choliz J, Eguizabal M, Hernandez-Solana A, 等. Comparison of
Algorithms for UWB Indoor Location and Tracking Systems; proceedings of
the 2011 IEEE 73rd Vehicular Technology Conference (VTC Spring), F 15-18
May 2011, 2011 [C].
[3] García E, Poudereux P, Á H, 等. A robust UWB indoor positioning
system for highly complex environments; proceedings of the 2015 IEEE
International Conference on Industrial Technology (ICIT), F 17-19 March
2015, 2015 [C].
[4] Deißler T, Janson M, Zetik R, 等. Infrastructureless indoor
mapping using a mobile antenna array; proceedings of the 2012 19th
International Conference on Systems, Signals and Image Processing
(IWSSIP), F 11-13 April 2012, 2012 [C].
[5] Gigl T, Janssen G J, Dizdarevic V, 等. Analysis of a UWB indoor
positioning system based on received signal strength; proceedings of the
2007 4th Workshop on Positioning, Navigation and Communication, F, 2007
[C]. IEEE.
[6] Alarifi A, Al-Salman A, Alsaleh M, 等. Ultra Wideband Indoor
Positioning Technologies: Analysis and Recent Advances [J]. Sensors
(Basel), 2016, 16 (5):
[7] Xue S, Yang Y. Positioning configurations with the lowest GDOP and
their classification [J]. Journal of Geodesy, 2014, 89 (1): 49-71.
[8] Wang C, Ning Y, Wang J, 等. Optimized deployment of anchors based
on GDOP minimization for ultra-wideband positioning [J]. Journal of
Spatial Science, 2020, 67 (3): 455-72.
[9] 王川阳. UWB定位方法及构型优化研究 [D]. 中国矿业大学, 2020.
[10] Press W H, Teukolsky S A, Vetterling W T, 等. Numerical recipes
3rd edition: The art of scientific computing [M]. Cambridge university
press, 2007.
[11] 朱向阳,熊有伦. 一种改进的Powell共轭方向算法 [J]. 控制与决策,
1996, (02): 304-8.
[12] 胡志刚. 北斗卫星导航系统性能评估理论与试验验证 [D]. 武汉大学,
2013.
[13] Xue S, Yang Y, Dang Y J J O G. A closed-form of Newton method for
solving over-determined pseudo-distance equations [J]. 2014, 88 (5):
441-8.
scientific computing [M]. Cambridge university
press, 2007.
[11] 朱向阳,熊有伦. 一种改进的Powell共轭方向算法 [J]. 控制与决策,
1996, (02): 304-8.
[12] 胡志刚. 北斗卫星导航系统性能评估理论与试验验证 [D]. 武汉大学,
2013.
[13] Xue S, Yang Y, Dang Y J J O G. A closed-form of Newton method for
solving over-determined pseudo-distance equations [J]. 2014, 88 (5):
441-8.