学习目标:
作为数值分析的基础内容,我建议你可以采取以下步骤来学习数值微分:
-
掌握微积分基础:数值微分是微积分中的一个分支,需要先掌握微积分基础知识,包括导数、极限、微分等。
-
学习数值微分的概念和方法:了解数值微分的定义、计算方法、误差分析等基础内容,包括前向差分、后向差分、中心差分等常用数值微分方法。
-
理解数值微分的误差和精度:掌握数值微分中误差的来源,包括截断误差、舍入误差等,了解误差的大小和影响因素,以及如何提高数值微分的精度。
-
学习数值微分的应用:数值微分在科学计算中有广泛的应用,如求解微分方程、计算数值积分、图像处理等。学习一些数值微分的应用案例,可以更好地理解数值微分的作用和价值。
-
练习数值微分的计算和编程:通过实践,加深对数值微分的理解和掌握,可以使用计算机编程语言如MATLAB、Python等实现数值微分的算法,并进行计算和比较。
总的来说,学习数值微分需要掌握一定的数学基础,理解数值计算的原理和方法,注重实践和编程能力的提高。

为什么有数值微分:
在实际问题中,有许多函数的解析式难以求得,甚至是无法求得的,而需要求解其导数值,例如在物理、工程、金融等领域的应用中常常需要求解某个函数在某个点处的导数值。由于导数的定义是极限,因此可以通过数值逼近导数值,这就是数值微分的基本思想。另外,有些函数在某些点处的导数不存在,但是可以用数值微分的方法求得近似值,这也是数值微分的应用之一。

5.1.1 利用插值多项式构造数值微分公式
利用插值多项式构造数值微分公式是一种常用的数值微分方法。其主要思想是通过在给定数据点处的函数值构造插值多项式,并利用其导数来逼近函数的导数。最常用的插值多项式是拉格朗日插值多项式,根据插值多项式的导数可得到数值微分公式。
以一阶数值微分为例,假设已知函数 $f(x)$ 在节点 $x_0,x_1$ 处的函数值 $f(x_0),f(x_1)$,则可以通过拉格朗日插值多项式构造出一个一阶数值微分公式。具体地,拉格朗日插值多项式为:
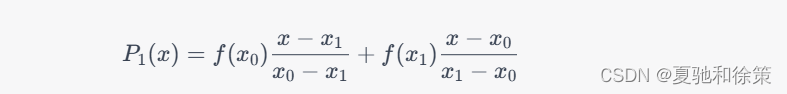
对其求导可得到:
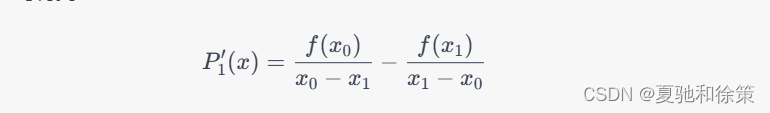
因此,可以将 $P'_1(x)$ 作为 $f'(x)$ 的近似,即
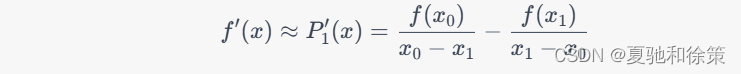
类似地,可以通过二阶拉格朗日插值多项式构造二阶数值微分公式,以此类推。
需要注意的是,插值多项式构造的数值微分公式存在截断误差,即由于采用有限个数据点进行插值,可能会出现插值误差。为了减小截断误差,可以采用更高阶的插值多项式或采用更密集的数据点。此外,还可以通过Richardson外推方法和龙贝格-李布曼算法等数值技巧来进一步提高数值微分的精度。


5.1.2 利用三次样条插值函数构造数值微分公式
利用三次样条插值函数构造数值微分公式的方法叫做三次样条插值微分法。它的主要思想是在每个小区间内,用三次多项式函数来近似替代被积函数,然后再对这些多项式函数进行求导,从而得到数值微分公式。
具体来说,三次样条插值函数的形式为:

其中,a_i,b_i,c_i,d_i是待定系数,x_i\leq x\leq x_{i+1}。
在每个小区间内,由于共有四个未知系数,需要确定四个条件才能唯一确定三次多项式函数,通常选用以下四个条件:
- 插值条件:S(x_i)=f(x_i)$和$S(x_{i+1})=f(x_{i+1})
- 连续性条件:S_i(x_{i+1})=S_{i+1}(x_{i+1})和S_i'(x_{i+1})=S_{i+1}'(x_{i+1})
其中,S_i'(x_{i+1})表示样条函数在x_{i+1}$处的一阶导数,S_i''(x_{i+1})表示样条函数在x_{i+1}处的二阶导数。
通过求解这些条件,可以得到系数a_i,b_i,c_i,d_i,进而得到三次样条插值函数$S(x)$。
接下来,对三次样条插值函数S(x)求导,可以得到数值微分公式,例如:
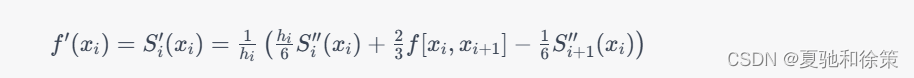
其中,h_i=x_{i+1}-x_i表示小区间的长度,f[x_i,x_{i+1}]表示f(x)在x_i和x_{i+1}处的差商。
总的来说,三次样条插值微分法的优点在于对函数进行了光滑的近似,具有较高的精度和稳定性。

总结:
数值微分的重点、难点和易错点如下:
重点:
- 数值微分是通过数值方法计算导数或高阶导数的一种方法。
- 常见的数值微分方法有差分法、插值法和曲线拟合法。
- 差分法是通过有限差分近似导数的方法,分为前向、后向和中心差分法。
- 插值法是通过利用已知函数值构造插值多项式来计算导数或高阶导数。
- 曲线拟合法是通过拟合曲线的导数或高阶导数来计算数值微分。
难点:
- 数值微分的精度和稳定性受到步长和截断误差的影响,需要进行适当的取舍。
- 差分法需要选择合适的差分格式和步长,过大或过小的步长都会影响精度。
- 插值法需要选择合适的插值点和插值多项式,过拟合或欠拟合都会影响精度。
- 曲线拟合法需要选择合适的拟合曲线类型和拟合点,不同的曲线类型对精度的影响有所不同。
易错点:
- 差分法中心差分法的计算需要注意步长取值和截断误差的影响。
- 插值法需要注意插值点的选择和插值多项式的次数,避免过度拟合或欠拟合。
- 曲线拟合法需要注意拟合点的选择和拟合曲线类型的选取,避免不稳定或过度拟合。
- 在实际应用中,需要根据具体问题选择合适的数值微分方法和参数,进行精度和稳定性的平衡。