系列文章目录

作者：i阿极

作者简介：Python领域新星作者、多项比赛获奖者：博主个人首页

😊😊😊如果觉得文章不错或能帮助到你学习，可以点赞👍收藏📁评论📒+关注哦！👍👍👍

📜📜📜如果有小伙伴需要数据集和学习交流，文章下方有交流学习区！一起学习进步！💪

---

专栏案例：机器学习案例
机器学习(一)：线性回归之最小二乘法
机器学习(二)：线性回归之梯度下降法
机器学习(三)：基于线性回归对波士顿房价预测
机器学习(十四)：基于逻辑回归对超市销售活动预测分析
机器学习(十五)：基于神经网络对用户评论情感分析预测
机器学习(十六)：线性回归分析女性身高与体重之间的关系
机器学习(十七)：基于支持向量机（SVM）进行人脸识别预测
机器学习(十八)：基于逻辑回归对优惠券使用情况预测分析
机器学习(十九）：基于逻辑回归对某银行客户违约预测分析
机器学习(二十)：基于朴素贝叶斯对花瓣花萼的宽度和长度分类预测

---

---

1、多项式贝叶斯算法原理

多项贝叶斯算法是贝叶斯分类算法的一种，适用于多类别离散型特征的分类问题。在多项贝叶斯算法中，假设每个类别$c$都有一组特征$x_1,x_2,\dots ,x_n$，这些特征都是离散型的，每个特征的取值为$x_{i,1},x_{i,2},\dots ,x_{i,k}$，其中$k$为第$i$个特征的取值数量。则多项贝叶斯算法通过以下公式计算后验概率：

$P\left(c\mid x_1,x_2,\dots ,x_n\right)=\frac{P(c){\prod }_{i=1}^{n}P\left(x_i\mid c\right)}{{\sum }_{c^{\prime }}P\left(c^{\prime }\right){\prod }_{i=1}^{n}P\left(x_i\mid c^{\prime }\right)}$

$P(c)$为类别$c$在训练数据集中的概率，$P(x_i|c)$为给定类别$c$时特征$x_i$的概率。

对于离散型特征，$P(x_i|c)$可以使用多项式分布来计算，即：

$P\left(x_i\mid c\right)=\frac{\mathrm{count}\left(x_i,c\right)+\alpha }{\mathrm{count}(c)+\alpha \times k_i}$

$count(x_i,c)$表示训练数据集中类别为$c$，特征$x_i$取值为$x_{i,j}$的样本数量，$count(c)$表示训练数据集中类别为$c$的样本数量，$k_i$表示第$i$个特征的取值数量，$\alpha$为拉普拉斯平滑系数，常取值为1。拉普拉斯平滑的作用是防止某些特征在某个类别下的取值为0，导致整个后验概率为0的情况发生。

通过计算后验概率，多项贝叶斯算法会将样本分到概率最大的类别中。在实际应用中，多项贝叶斯算法常用于文本分类、垃圾邮件识别等问题。

2、模型举例理解

为了更好的理解$P(x_i|c)$公式，通过例子来实现。

假设影响女孩是否参加相亲活动的重要因素有三个，分别是男孩的职业、受教育水平和收入状况；如果女孩参加相亲活动，则对应的Meet变量为1，否则为0。

职务	学历	收入	是否参加
公务员	本科	中	1
公务员	本科	低	1
非公务员	本科	中	0
非公务员	本科	高	1
公务员	硕士	中	1
非公务员	本科	低	0
公务员	本科	高	1
非公务员	硕士	低	0
非公务员	硕士	中	0
非公务员	硕士	高	1

我们的目标是：对于高收入的公务员，并且其学历为硕士的男生来说，女孩是否愿意参与他的相亲。使用多项式贝叶斯分类器实现。

首先，计算因变量各类别频率：

$\begin{array}{l}P(\text{ Meet }=0)=4/10=0.4\\ P(\text{ Meet }=1)=6/10=0.6\end{array}$

其次，计算单变量条件概率：

$\begin{array}{l}P(\text{ Occupation }=\text{ 公务员 }\mid \text{ Meet }=0)=\frac{0+1}{4+2\times 1}=\frac{1}{6}\\ P(\text{ Occupation }=\text{ 公务员 }\mid \text{ Meet }=1)=\frac{4+1}{6+2\times 1}=\frac{5}{8}\\ P(\text{ Edu }=\text{ 硕士 }\mid \text{ Meet }=0)=\frac{2+1}{4+2\times 1}=\frac{3}{6}\\ P(\text{ Edu }=\text{ 硕 }士\mid \text{ Meet }=1)=\frac{2+1}{6+2\times 1}=\frac{3}{8}\\ P(\text{ Income }=\text{ 高 }\mid \text{ Meet }=0)=\frac{0+1}{4+2\times 1}=\frac{1}{6}\\ P(\text{ Income }=\text{ 高 }\mid \text{ Meet }=1)=\frac{3+1}{6+2\times 1}=\frac{4}{8}\end{array}$

最后，计算贝叶斯后验概率：

$P(\text{Meet }=0\mid \text{ Occupation }=\text{ 公务员 },\text{ Edu }=硕士,\text{Income}=高)=\frac{4}{10}\times \frac{1}{6}\times \frac{3}{6}\times \frac{1}{6}=\frac{1}{180}$
$P(\text{Meet }=1\mid \text{ Occupation }=\text{ 公务员 },\text{ Edu }=硕士,\text{Income}=高)=\frac{6}{10}\times \frac{5}{8}\times \frac{3}{8}\times \frac{4}{8}=\frac{18}{256}$

由结果得，当男生为高收入的公务员，并且受教育水平也很高时，女生愿意见面的概率约为0.0703、不愿意见面的概率约为0.0056。所以根据$argmaxP(C_i)P(X|C_i)$的原则，最终女生会选择参加这位男生的相亲。

3、实验环境

Python 3.9

Anaconda

Jupyter Notebook

4、多项式贝叶斯模型-蘑菇毒性判别

4.1数据说明

数据集信息：

该数据集包括对应于姬松茸和鳞片菌科 23 种有鳃蘑菇的假设样本的描述（第 500-525 页）。每个物种都被确定为绝对可食用、绝对有毒或未知可食性且不推荐。后一类与有毒的一类结合在一起。该指南明确指出，没有简单的规则来确定蘑菇的可食用性；对于毒橡树和常春藤，没有像“传单三，顺其自然”这样的规则。

属性信息：
1.cap-shape: bell=b,conical=c,convex=x,flat=f, knobbed=k,sunken=s
2.cap-surface: fibrous=f,grooves=g,scaly=y,smooth=s
3.cap-color: brown=n,buff=b,cinnamon=c,gray=g,green=r, pink=p,purple=u,red=e,white=w,yellow=y
4.bruises?: bruises=t,no=f
5. odor: almond=a,anise=l,creosote=c,fishy=y,foul=f, musty=m,none=n,pungent=p,spicy=s
6. gill-attachment: attached=a,descending=d,free=f,notched=n
7. gill-spacing: close=c,crowded=w,distant=d
8. gill-size: broad=b,narrow=n
9. gill-color: black=k,brown=n,buff=b,chocolate=h,gray=g, green=r,orange=o,pink=p,purple=u,red=e, white=w,yellow=y
10. stalk-shape: enlarging=e,tapering=t
11. stalk-root: bulbous=b,club=c,cup=u,equal=e, rhizomorphs=z,rooted=r,missing=?
12. stalk-surface-above-ring: fibrous=f,scaly=y,silky=k,smooth=s
13. stalk-surface-below-ring: fibrous=f,scaly=y,silky=k,smooth=s
14. stalk-color-above-ring: brown=n,buff=b,cinnamon=c,gray=g,orange=o, pink=p,red=e,white=w,yellow=y
15. stalk-color-below-ring: brown=n,buff=b,cinnamon=c,gray=g,orange=o, pink=p,red=e,white=w,yellow=y
16. veil-type: partial=p,universal=u
17. veil-color: brown=n,orange=o,white=w,yellow=y
18. ring-number: none=n,one=o,two=t
19.ring-type: cobwebby=c,evanescent=e,flaring=f,large=l, none=n,pendant=p,sheathing=s,zone=z
20. spore-print-color: black=k,brown=n,buff=b,chocolate=h,green=r, orange=o,purple=u,white=w,yellow=y
21. population: abundant=a,clustered=c,numerous=n, scattered=s,several=v,solitary=y
22. habitat: grasses=g,leaves=l,meadows=m,paths=p, urban=u,waste=w,woods=d

4.2数据准备

导入数据

# 导入第三方包
import pandas as pd
# 读取数据
mushrooms = pd.read_csv(r"D:\CSDN\machine learning\data\mushrooms.csv")
# 数据的前5行
mushrooms.head()

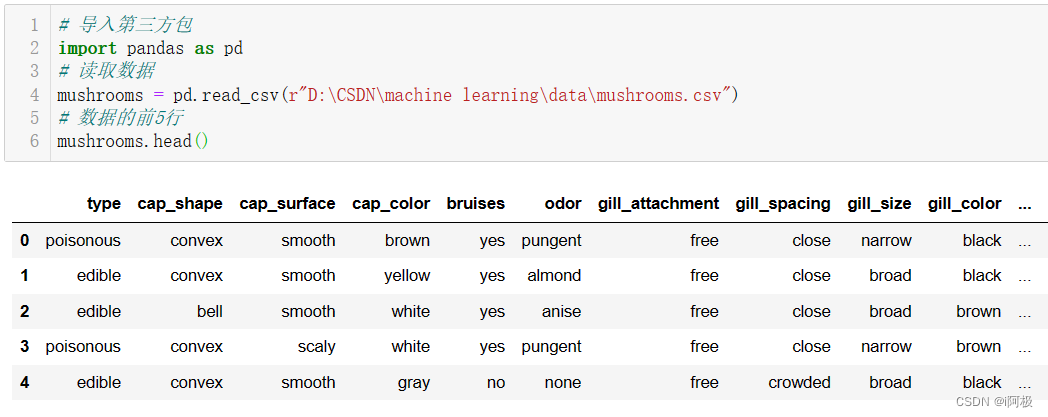
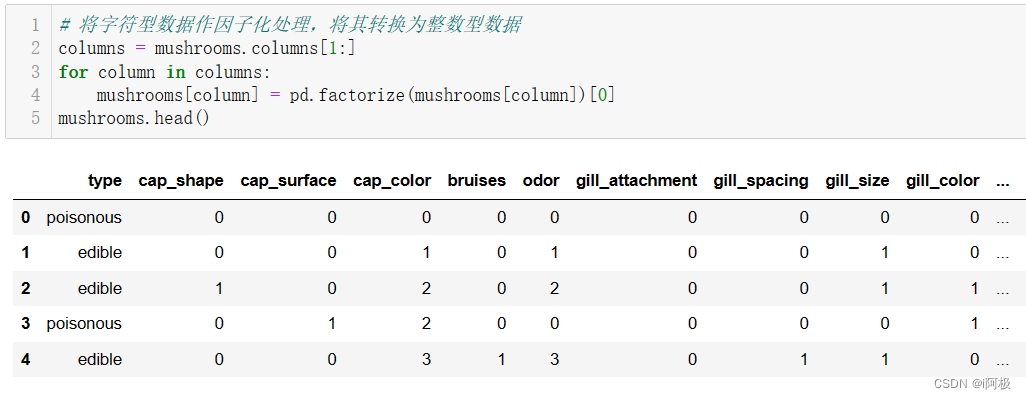
将字符型数据作因子化处理，将其转换为整数型数据

columns = mushrooms.columns[1:]
for column in columns:
    mushrooms[column] = pd.factorize(mushrooms[column])[0]
mushrooms.head()

4.3划分训练集和测试集

from sklearn import model_selection
# 将数据集拆分为训练集合测试集
Predictors = mushrooms.columns[1:]
X_train,X_test,y_train,y_test = model_selection.train_test_split(mushrooms[Predictors], mushrooms['type'], 
                                                                 test_size = 0.25, random_state = 10)

4.4多项式贝叶斯模型建立

from sklearn import naive_bayes
from sklearn import metrics
import seaborn as sns
import matplotlib.pyplot as plt
# 构建多项式贝叶斯分类器的“类”
mnb = naive_bayes.MultinomialNB()
# 基于训练数据集的拟合
mnb.fit(X_train, y_train)
# 基于测试数据集的预测
mnb_pred = mnb.predict(X_test)

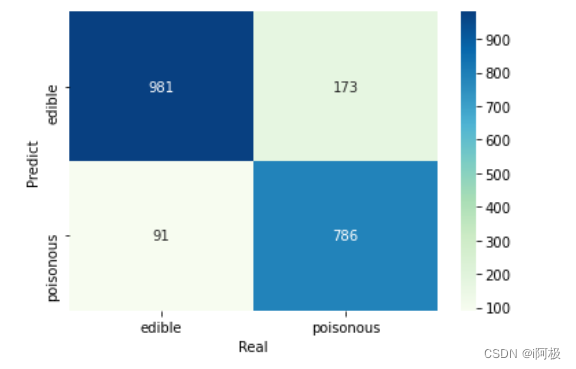
4.5绘制混淆矩阵

mnb_pred = mnb.predict(X_test)
# 构建混淆矩阵
cm = pd.crosstab(mnb_pred,y_test)
# 绘制混淆矩阵图
sns.heatmap(cm, annot = True, cmap = 'GnBu', fmt = 'd')
# 去除x轴和y轴标签
plt.xlabel('Real')
plt.ylabel('Predict')
# 显示图形
plt.show()

4.6查看模型预测的准确率

# 模型的预测准确率
print('模型的准确率为：\n',metrics.accuracy_score(y_test, mnb_pred))
print('模型的评估报告：\n',metrics.classification_report(y_test, mnb_pred))

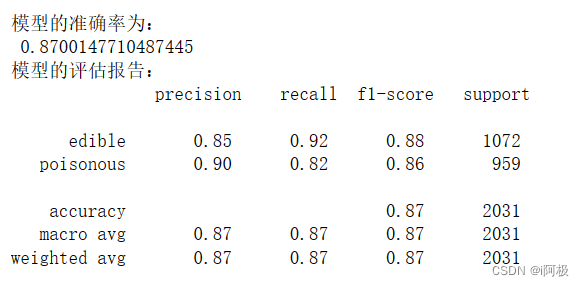
由图发现，模型在测试数据集上的整体预测准确率为87%，无毒蘑菇的预测覆盖率为92%，有毒蘑菇的预测覆盖率为82%。

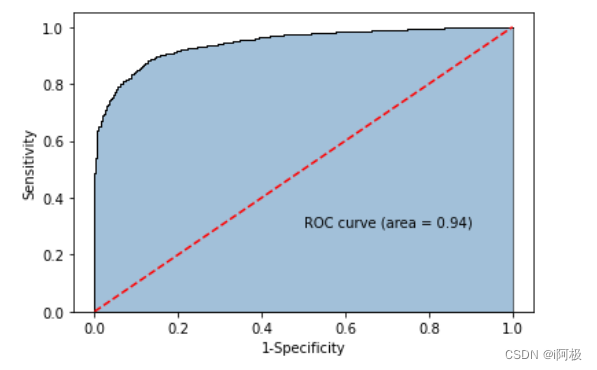
4.7计算正例的预测概率，用于生成ROC曲线的数据

from sklearn import metrics
# 计算正例的预测概率，用于生成ROC曲线的数据
y_score = mnb.predict_proba(X_test)[:,1]
fpr,tpr,threshold = metrics.roc_curve(y_test.map({'edible':0,'poisonous':1}), y_score)
# 计算AUC的值
roc_auc = metrics.auc(fpr,tpr)

# 绘制面积图
plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black')
# 添加边际线
plt.plot(fpr, tpr, color='black', lw = 1)
# 添加对角线
plt.plot([0,1],[0,1], color = 'red', linestyle = '--')
# 添加文本信息
plt.text(0.5,0.3,'ROC curve (area = %0.2f)' % roc_auc)
# 添加x轴与y轴标签
plt.xlabel('1-Specificity')
plt.ylabel('Sensitivity')
# 显示图形
plt.show()

---

总结

对于离散型自变量的数据集而言，在分类问题上并非都可以使用多项式贝叶斯分类器，如果自变量在特定y值下的概率不服从多项式分布的话，分类器的效果是不理想的。通常情况下，会利用多项式贝叶斯模型作文本分类，如判断邮件是否为垃圾邮件，用户评论是否为正面等等。

📢文章下方有交流学习区！一起学习进步！💪💪💪
📢首发CSDN博客，创作不易，如果觉得文章不错，可以点赞👍收藏📁评论📒
📢你的支持和鼓励是我创作的动力❗❗❗