一本通 3.4.4 并查集

1346：【例4-7】亲戚(relation)

【题目描述】

或许你并不知道，你的某个朋友是你的亲戚。他可能是你的曾祖父的外公的女婿的外甥女的表姐的孙子。如果能得到完整的家谱，判断两个人是否是亲戚应该是可行的，但如果两个人的最近公共祖先与他们相隔好几代，使得家谱十分庞大，那么检验亲戚关系实非人力所能及。在这种情况下，最好的帮手就是计算机。为了将问题简化，你将得到一些亲戚关系的信息，如Marry和Tom是亲戚，Tom和Ben是亲戚，等等。从这些信息中，你可以推出Marry和Ben是亲戚。请写一个程序，对于我们的关于亲戚关系的提问，以最快的速度给出答案。

【题目分析】

一般并查集的执行过程，查find函数带路径压缩，并union函数将左侧归顺右侧，查询功能如果两个点的祖先不是同一个输出No，否则输出Yes
特别的：输入输出数据较大，使用scanf与printf函数

【代码实现】

#include<bits/stdc++.h>
using namespace std;

int fa[20005], x, y;

int get(int a) {
	return fa[a] == a ? a : fa[a] = get(fa[a]);
}
void join(int a, int b) {
	int fa_a = get(a);
	int fa_b = get(b);
	if (fa_a != fa_b) fa[fa_a] = fa_b;
}
int main() {
	int n, m;
	cin >> n >> m;
	for (int i = 1; i <= n; i++) {
		fa[i] = i;
	}
	for (int i = 1; i <= m; i++) {
		scanf("%d%d", &x, &y);
		join(x, y);
	}
	cin >> m;
	for (int i = 1; i <= m; i++) {
		scanf("%d%d", &x, &y);
		if (get(x) == get(y)) printf("Yes\n");
		else printf("No\n");
	}
	return 0;
}

1347：【例4-8】格子游戏

【题目描述】

Alice和Bob玩了一个古老的游戏：首先画一个n × n的点阵（下图n = 3）

接着，他们两个轮流在相邻的点之间画上红边和蓝边：

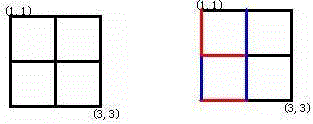
直到围成一个封闭的圈（面积不必为1）为止，“封圈”的那个人就是赢家。因为棋盘实在是太大了(n ≤ 200)，他们的游戏实在是太长了！他们甚至在游戏中都不知道谁赢得了游戏。于是请你写一个程序，帮助他们计算他们是否结束了游戏？

【题目分析】

并查集找环：将一条边进行合并时，首先判断边的两个端点是否属于同一个集合，如果是，已经存在环，否则不存在环，合并两点的祖先。

特别的：本题中的对象不是单个数值是点数据，需要定义点的结构体进行存储，初始化将二维数组的编号与存储的点对应相等，判断时需要同时满足x、y都相等才说明祖先相同（也可以使用pair存储）。

【代码实现】

#include <bits/stdc++.h>
using namespace std;

int n, m;
struct Point {
	int x;
	int y;
} father_p[205][205], p1, p2;

Point find(Point p) {
	int x = p.x;
	int y = p.y;
	if (father_p[x][y].x == x && father_p[x][y].y == y) return p;
	else {
		return father_p[x][y] = find(father_p[x][y]);
	}
}
void unionn(Point p1, Point p2) {
	Point fa_p1 = find(p1);
	Point fa_p2 = find(p2);
	if (fa_p1.x != fa_p2.x || fa_p1.y != fa_p2.y) {
		int x = p2.x;
		int y = p2.y;
		father_p[x][y] = fa_p1;
	}
}
int main() {
	//input data
	//clock_t s = clock();
	cin >> n >> m;
	//init
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= n; j++) {
			father_p[i][j].x = i;
			father_p[i][j].y = j;
		}

	for (int i = 1; i <= m; i++) {
		int x, y;
		char c;
		cin >> x >> y >> c;
		if (c == 'D') {
			Point pp;
			pp.x = x;
			pp.y = y;
			p1 = find(pp);
			pp.x = x + 1;
			pp.y = y;
			p2 = find(pp);
		}
		if (c == 'R') {
			Point pp;
			pp.x = x;
			pp.y = y;
			p1 = find(pp);
			pp.x = x;
			pp.y = y + 1;
			p2 = find(pp);
		}

		if (p1.x == p2.x && p1.y == p2.y) {
			cout << i << endl;
			return 0;
		} else {
			unionn(p1, p2);
		}
	}
	cout << "draw" << endl;

	//output time
	//cout <<endl<< clock() - s<<endl;
	return 0;
}

1385：团伙(group)

【题目描述】

在某城市里住着n个人，任何两个认识的人不是朋友就是敌人，而且满足：

1、我朋友的朋友是我的朋友；

2、我敌人的敌人是我的朋友；

所有是朋友的人组成一个团伙。告诉你关于这n个人的m条信息，即某两个人是朋友，或者某两个人是敌人，请你编写一个程序，计算出这个城市最多可能有多少个团伙？

【题目分析】

扩展域并查集：将点x进行分解，x表示x本身，x+n表示x的敌人，y表示y本身，y+n表示y的敌人，如果x与y时朋友需要将x和y合并，x+n与y+n合并，如果x与y是敌人，需要将x+n与y合并，x与y+n合并。

特别的：定义祖先数组时需要扩展2倍，判断团伙数量只需要查找fa[i]==i的数量

【代码实现】

#include<bits/stdc++.h>
#define N 100001
using namespace std;
int f[N], d[N], n, m;
int find(int x) {
	return f[x] == x ? x : f[x] = find(f[x]);
}
void fun(int x, int y) {
	x = find(x);
	y = find(y);
	if (x != y)
		f[y] = x;
}
int main() {
	cin >> n >> m;
	for (int i = 1; i <= n * 2; i++) {
		f[i] = i;
	}
	for (int i = 1; i <= m; i++) {
		int z, x, y;
		cin >> z >> x >> y;
		if (z == 0)fun(x, y);
		else if (z == 1)fun(x + n, y), fun(x, y + n);
	}
	int sum = 0;
	for (int i = 1; i <= n; i++) {
		int z = find(i);
		if (!d[z]) {
			d[z] = 1;
			sum++;
		}
	}
	cout << sum;
	return 0;
}

1386：打击犯罪(black)

【题目描述】

某个地区有n(n<=1000)个犯罪团伙，当地警方按照他们的危险程度由高到低给他们编号为1-n，他们有些团伙之间有直接联系，但是任意两个团伙都可以通过直接或间接的方式联系，这样这里就形成了一个庞大的犯罪集团，犯罪集团的危险程度由集团内的犯罪团伙数量唯一确定，而与单个犯罪团伙的危险程度无关（该犯罪集团的危险程度为n）。现在当地警方希望花尽量少的时间（即打击掉尽量少的团伙），使得庞大的犯罪集团分离成若干个较小的集团，并且他们中最大的一个的危险程度不超过n/2。为达到最好的效果，他们将按顺序打击掉编号1到k的犯罪团伙，请编程求出k的最小值。

【题目分析】

带权并查集
正向思维：使用邻接矩阵存储连边关系，从1~n枚举去掉1-k的点（k的范围从1-n），查询最大集合点数是否不超过n/2，则为答案，每次枚举都要重置并查集，时间复杂度：O(n^3)
逆向思考：n ~ 1枚举，每次把K加入图中，也就是删除1 ~ K-1,剩余k ~ n,若最大集合点不超过N/2这个方案可行还可能更小，一旦不满足就是不能再加K，即K 要删掉，就输出答案。时间复杂度：O(n^3)

【代码实现】

#include <bits/stdc++.h>
using namespace std;

int n, m;
int father[1005];
int group_num[1005];
vector<int > group[1005];

int find(int x) {
	if (father[x] != x)
		father[x] = find(father[x]); //路径压缩
	return  father[x];
}
void unionn(int x, int y) {
	int fa_x = find(x);
	int fa_y = find(y);
	if (fa_x != fa_y) {
		father[fa_y] = fa_x;
		int nfx = group_num[fa_x];
		int nfy = group_num[fa_y];
		group_num[fa_x] += nfy;
		group_num[fa_y] += nfx;
	}

}
int main() {
	cin >> n;
	for (int i = 1; i <= n; i++) {
		father[i] = i;
		group_num[i] = 1;
	}
	for (int i = 1; i <= n; i++) {
		int p, x;
		cin >> p;
		group[i].push_back(p);
		for (int j = 1; j <= p; j++) {
			cin >> x;
			group[i].push_back(x);
		}
	}

	for (int i = n; i >= 1; i--) {
		for (int j = 1; j < (int)group[i].size(); j++) {
			if (group[i][j] >= i) {
				unionn(group[i][j], i);
				for (int k = 1; k <= n; k++) {
					if (group_num[k] > (n >> 1)) {
						cout << i;
						return 0;
					}
				}
			}
		}
	}

	return 0;
}

1387：搭配购买(buy)

【题目描述】

Joe觉得云朵很美，决定去山上的商店买一些云朵。商店里有n朵云，云朵被编号为1，2，…，n，并且每朵云都有一个价值。但是商店老板跟他说，一些云朵要搭配来买才好，所以买一朵云则与这朵云有搭配的云都要买。

但是Joe的钱有限，所以他希望买的价值越多越好。

【题目分析】

带权并查集：使用并查集算出每个云朵集合的最大价值和花费，使用0-1背包进行问题求解

定义fa[]数组存储云朵的祖先，value[]数组存储云朵所在集合的价值，money[]数组存储云朵所在集合的花费.
使用并查集合并云朵集合，得到每个集合的价值和花费，例如将a合并到b中，yuan[fa[b]].value+=yuan[fa[a]].value yuan[fa[b]].money +=yuan[fa[a]].money
检查所有并查集获得云朵集合的价值value[]和费用money[]，个数为cnt，总钱数为w，使用0-1背包求解最大价值dp[w]
for(i=1;i<=cnt;i++)
for(j=w;j>=dc[i];j--)
dp[j]=max(dp[j],dp[j-money[i]]+value[i])

【代码实现】

#include <bits/stdc++.h>
using namespace std;

int n, m, w;
const int maxn = 10005;
int money[maxn], value[maxn], dp[maxn];
struct Yun {
	int father;
	int money;
	int value;
} yun[maxn];

int find(int y) {
	if (yun[y].father != y) {
		yun[y].father = find(yun[y].father);
	}
	return yun[y].father;
}

bool cmp(const Yun& a, const Yun& b) {
	return a.value > b.value;
}
int main() {
	//input data
	//clock_t s = clock();
	cin >> n >> m >> w;

	for (int i = 1; i <= n; i++) {
		yun[i].father = i;
		cin >> yun[i].money;
		cin >> yun[i].value;
	}

	for (int i = 1; i <= m; i++) {
		int x, y;
		cin >> x >> y;
		int fa_x = find(x);
		int fa_y = find(y);
		if (fa_x != fa_y) {
			yun[fa_y].father = fa_x;
			yun[fa_y].money += yun[fa_x].money;
			yun[fa_x].money = yun[fa_y].money;
			yun[fa_y].value += yun[fa_x].value;
			yun[fa_x].value = yun[fa_y].value;
		}
	}
	int cnt = 0;
	for (int i = 1; i <= n; i++) {
		if (yun[i].father == i) {
			money[++cnt] = yun[i].money;
			value[cnt]  = yun[i].value;
		}
	}



	for (int i = 1; i <= cnt; i++) {
		for (int j = w; j >= money[i]; j--) {
			dp[j] = max(dp[j], dp[j - money[i]] + value[i]);
		}
	}
//	sort(yun+1, yun + n+1, cmp);
	cout << dp[w];
	return 0;
}

1388：家谱(gen)

【题目描述】

现代的人对于本家族血统越来越感兴趣，现在给出充足的父子关系，请你编写程序找到某个人的最早的祖先。

【题目分析】

问题本质：给定合并顺序的并查集

定义关联容器map数组 fa[]存储字符串，获取每一行字符判断第一个字符如果为#，分割字符串fat，初始化fa[fat]=fat，如果为+，分割字符串son，指定son的父亲节点fa[son]=find(fat)，如果为？，分割字符串son，输出查询结果fa[son]，如果为$，结束运行

【代码实现】

#include <bits/stdc++.h>
using namespace std;

map<string, string > father;

string find(string s) {
	if (father[s] != s)
		father[s] = find(father[s]);
	return father[s];
}

int main() {
	//input data
	//clock_t s = clock();
	string in;
	string fa;
	string son;
	string que;
	while (cin >> in, in != "$") {
		if (in[0] == '#') {
			fa = in.substr(1);
			if (father[fa] == "") father[fa] = fa;
		}
		if (in[0] == '+') {
			son = in.substr(1);
			father[son] = find(fa);
		}
		if (in[0] == '?') {
			que = in.substr(1);
			cout << que << " " << find(que) << endl;
		}
	}
	//output time
	//cout <<endl<< clock() - s<<endl;
	return 0;
}

1389：亲戚

【题目描述】

若某个家族人员过于庞大，要判断两个是否是亲戚，确实还很不容易，现在给出某个亲戚关系图，求任意给出的某个人所在家族的人数。

规定：x和y是亲戚，y和z是亲戚，那么x和z也是亲戚。如果x,y是亲戚，那么x的亲戚都是y的亲戚，y的亲戚也都是x的亲戚。

【题目分析】

带权并查集：集合元素包含家族人数，询问某个人先找到该人的祖先，并输出祖先的人数

定义并查集关联数组fa[]，集合个数数组sum[]，获取关系字符c，如果c=='M',将a合并给b，sum[fa_b]+=sum[fa_a],如果c=='Q',输出sum[fa_q]

【代码实现】

#include <bits/stdc++.h>
using namespace std;

int father[100005];
int sum[100005];
int n, m;
int find(int x) {
	if (father[x] != x)
		father[x] = find(father[x]);
	return father[x];
}

int main() {
	//input data
	//clock_t s = clock();
	cin >> n >> m;
	for (int i = 1; i <= n; i++) {
		father[i] = i;
		sum[i] = 1;
	}
	
	for (int i = 1; i <= m; i++) {
		char c;
		int a, b;
		scanf("%c",&c);scanf("%c",&c);
		if (c == 'M') {
			scanf("%d%d", &a, &b);
			int fa_a = find(a); 
			int fa_b = find(b);
			if (fa_a != fa_b) {
				father[fa_b] = fa_a;
				sum[fa_a] += sum[fa_b];
			}
		} 
		if(c=='Q') {
			scanf("%d", &a);
			printf("%d\n", sum[find(a)]);
		}
	}

	//output time
	//cout <<endl<< clock() - s<<endl;
	return 0;
}

1390：食物链【NOI2001】

【题目描述】

动物王国中有三类动物A,B,C，这三类动物的食物链构成了有趣的环形。A吃B， B吃C，C吃A。

现有N个动物，以1－N编号。每个动物都是A,B,C中的一种，但是我们并不知道它到底是哪一种。

有人用两种说法对这N个动物所构成的食物链关系进行描述：

第一种说法是"1 X Y"，表示X和Y是同类。

第二种说法是"2 X Y"，表示X吃Y。

此人对N个动物，用上述两种说法，一句接一句地说出K句话，这K句话有的是真的，有的是假的。当一句话满足下列三条之一时，这句话就是假话，否则就是真话。

1）当前的话与前面的某些真的话冲突，就是假话；

2）当前的话中X或Y比N大，就是假话；

3）当前的话表示X吃X，就是假话。

你的任务是根据给定的N（1≤ N ≤50,000）和K句话（0≤K≤100,000），输出假话的总数。

【题目分析】

扩展域并查集：将x进行关系分解，x表示自身，x+n表示x的食物，x+2*n表示x的敌人，同样y表示自身，y+n表示x的食物，y+2*n表示x的敌人

x与y是同类，如果x能够吃掉y或者y能够吃掉x，该命题都为假，find(x+n)==find(y)||find(y+n)==find(x)
否则合并x与y，合并x+n与y+n，合并x+2*n与y+2*n
x可以吃掉y，如果x与y是同类或者y可以吃掉x，该命题都为假，find(x)==find(y)||find(y+n)==find(x)
否则合并x+n与y，合并x与y+2*n，合并x+2*n与y+n

统计假命题的个数进行答案输出

【代码实现】

#include<bits/stdc++.h>
using namespace std;


int fa[150005], x, y, p;

int get(int a) {
	return fa[a] == a ? a : fa[a] = get(fa[a]);
}
void join(int a, int b) {
	int fa_a = get(a);
	int fa_b = get(b);
	if (fa_a != fa_b) fa[fa_a] = fa_b;
}

int main() {

	int m, n;
	cin >> n >> m;
	for (int i = 1; i <= 3 * n; i++) {
		fa[i] = i;
	}
	int ans = 0;
	for (int i = 1; i <= m; i++) {
		cin >> p >> x >> y;
		if (x > n || y > n) ans++;
		else if (p == 2 && x == y) ans++;
		else {
			if (p == 1) {
				if (get(x + n) == get(y) || get(x) == get(y + n)) ans++;
				else join(x, y), join(x + n, y + n), join(x + 2 * n, y + 2 * n);

			} else {
				if (get(x) == get(y) || get(x) == get(y + n)) ans++;
				else join(x + n, y), join(x, y + 2 * n), join(x + 2 * n, y + n);
			}
		}
	}
	cout << ans << endl;
	return 0;
}