信息论与编码：随参信道特性

文章目录

- - 随参信道数学模型的建立
  - 随参信道对信号传输的影响
  - - 平坦性衰落及频率选择性衰落
    - 1.平坦性衰落
    - - Rayleigh 分布
      - Rice 分布
    - 2.频率选择性衰落
  - 多径随参信道的时延扩展与相干带宽
  - - 随参信道的多径时延特性
    - 多径信道的频域特性
  - 移动信道的多普勒扩展及相干时间
  - - 1.多普勒扩展
    - 2.信道的相干时间 Tc 和多普勒频率扩展
    - 3.多普勒扩展对衰落的影响
    - 4.同时考虑随参信道的多径时延扩展及多普勒扩展对衰落的影响
    - 5.抗衰落的方案
- 总结

随参信道的传输特性主要依赖于传输媒质特性，以电离层反射信道、对流层散射信道为主要代表。 随参信道是一种信道传输特性随时间随机快速变化的信道，包括陆地移动信道，短波电离层反射信道、超短波微波对流层散射信道、超短波视距绕射信道。

随参信道的传输媒介具有以下三个特点：

对信号的衰耗（衰减）随时间而变；
传输的时延随时间而变；
会产生多径传播的效果。

多径传播 ：指由发射点出发的电波可能经过多条路径到达接收点。每条路径对信号的衰减和时延都随电离层或对流层等传输媒质的变化而变化，接收信号将是衰减和时延随时间变化的各路径信号的叠加与合成。
$h(t)=\sum_{i=1}^{L} \mu_{i}(t) \delta\left[t-\tau_{i}(t)\right]$

随参信道数学模型的建立

设发送信号为 $\sum_{n=-\infty}^{\infty} d_{n} g(t-n T) \cos 2 \pi f_{c} c t$ , $A$ 信号幅度, $d_{n}$ 信息码元, $g (t)$ 信息码元波形, $f_{c}$ 载波频率。
令 $b(t)=\sum_{n=-\infty}^{\infty} d_{n} g(t-n T)$ , 则 $\cos 2 \pi f_{c} t$ 。经过多径信道 $h(t)=\sum_{i=1}^{L} u_{i}(t) \delta\left(t-\tau_{i}(t)\right)$ , 接收信号为
$\sum_{i=1}^{L} u_{i}(t) b\left(t-\tau_{i}(t)\right) \cos \left(2 \pi f_{c} t+\varphi_{i}(t)\right)$
$u_{i}(t)$ 第 i 条路径的衰落因子, $\tau_{i}(t)$ 为第 i 条路径的传输时延。

令 $\varphi_{i}(t)=-2 \pi f_{c} \tau_{i}(t)$ , 则有
$\sum_{i=1}^{L} u_{i}(t) b\left(t-\tau_{i}(t)\right) \cos \left(2 \pi f_{c}\left(t-\tau_{i}(t)\right)\right)$
一般情况 $u_{i}(t)$ 、 $\tau_{i}(t)$ 较载波 $\cos \left(2 \pi f_{c} t\right)$ 变化缓慢得多, $r (t)$ 可视为窄带过程, 又可表示为
$\begin{array}{c} r(t)=A \sum_{i=1}^{L} u_{i}(t) b\left(t-\tau_{i}(t)\right) \cos \varphi_{i}(t) \cos 2 \pi f_{c} t \\ -A \sum_{i=1}^{L} u_{i}(t) b\left(t-\tau_{i}(t)\right) \sin \varphi_{i}(t) \sin 2 \pi f_{c} t \end{array}$
即为随参信道的数学模型, 利用它可以分析随参信道对信号传输的影响。

随参信道对信号传输的影响

平坦性衰落及频率选择性衰落

1.平坦性衰落

满足: $\left|\tau_{i}(t)\right|_{\max } \ll T$ , $T $ 为码元周期, 且 $\left|\tau_{i}(t)\right|_{\max } \sim 1 / f_{c}$ $b\left(t-\tau_{i}(t)\right) \approx b(t-\overline{\tau(t)}), i=1,2, \ldots, L$ , 其中 $\overline{\tau(t)}$ 为 $\tau_{i}(t)$ 的数学期望。
$\begin{aligned} r(t) &=A \sum_{i=1}^{L} u_{i}(t) b\left(t-\tau_{i}(t)\right) \cos \varphi_{i}(t) \cos 2 \pi f_{c} t-A \sum_{i=1}^{L} u_{i}(t) b\left(t-\tau_{i}(t)\right) \sin \varphi_{i}(t) \sin 2 \pi f_{c} t \\ &=A b(t-\overline{\tau(t)})\left[x_{c}(t) \cos 2 \pi f_{c} t-x_{s}(t) \sin 2 \pi f_{c} t\right]=A b(t-\overline{\tau(t)}) v(t) \cos \left(2 \pi f_{c} t+\varphi(t)\right) \\ &=\operatorname{Re}\left[A b(t-\overline{\tau(t)}) v(t) e^{j\left(2 \pi f_{c} t+\varphi(t)\right)}\right] \end{aligned}$
其中 $v (t)$ 为 $r (t)$ 的随机包络, $\varphi(t)$ 为 $r (t)$ 的随机相位。
$\begin{aligned} x_{c}(t) &=\sum_{i=1}^{L} u_{i}(t) \cos \varphi_{i}(t) \\ x_{s}(t) &=\sum_{i=1}^{L} u_{i}(t) \sin \varphi_{i}(t) \\ v(t) &=\sqrt{x_{c}^{2}(t)+x_{s}^{2}(t)} \\ \varphi(t) &=\arctan \left(\frac{x_{s}(t)}{x_{c}(t)}\right) \end{aligned}$

$r(t)=\operatorname{Re}\left[A b(t-\overline{\tau(t)}) v(t) e^{j\left(2 \pi f_{c} t+\varphi(t)\right)}\right]$

多径传输和信道特性的变化导致接收信号幅度随机变化, 载波相位随机变化, 而基带信号 $\boldsymbol{b}(t)$ 波形变化不大。—平坦性衰落

多径传输引起的复包络 $e^{j \varphi(t)}$ 对基带信号而言相当于乘性千扰。

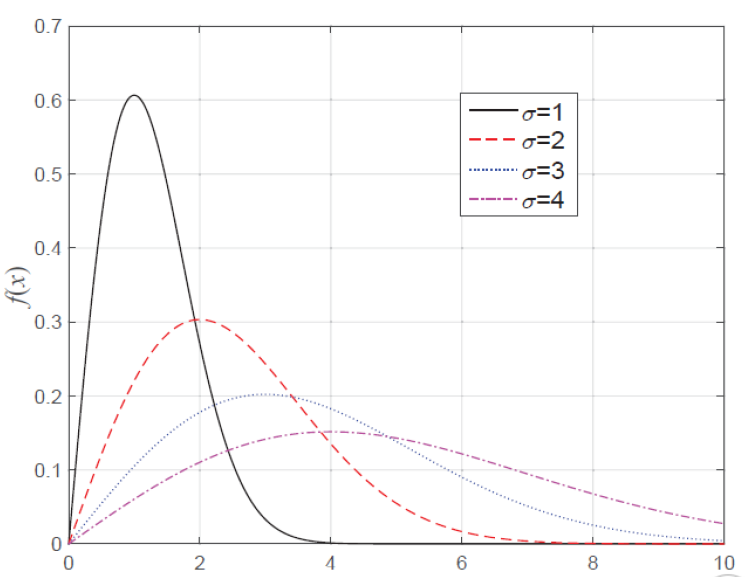
经不同路径到达接收端的不同信号的相关性很小，且根据中心极限定理, 当路径数很大时, 多径信号的概率分布趋于高斯分布, 即 $x_{s}$ ， $x_{c}$ 服从高斯分布，从而 v(t) 的概率分布为瑞利（Rayleigh）分布, 相位 $\varphi(t)$ 为均匀分布。另外, 如果接收信号中还包括一路直射信号 , 则信号的包络分布为广义瑞利分布或者莱斯 (Rice) 分布。

Rayleigh 分布

$f(x)=\frac{x}{\sigma^{2}} e^{-\frac{x^{2}}{2 \sigma^{2}}}$

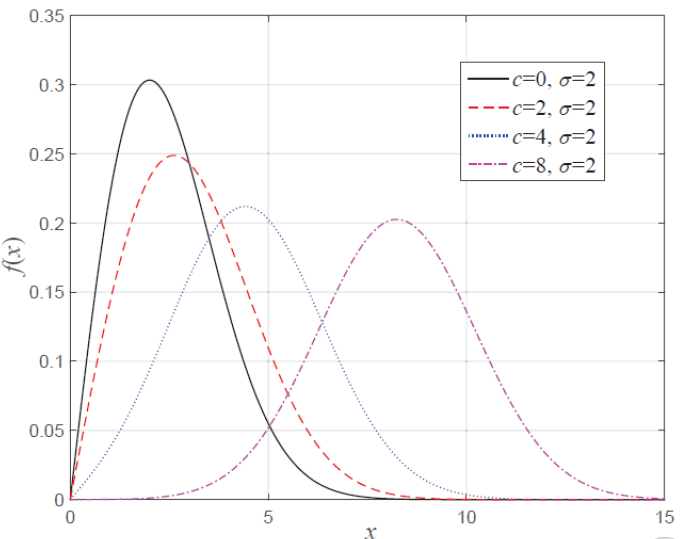
Rice 分布

$f(x)=\frac{x}{\sigma^{2}} e^{-\frac{x^{2}+c^{2}}{2 \sigma^{2}}} I_{0}\left(\frac{c x}{\sigma^{2}}\right)$

其中 c 为直射 (视距) 信号的峰值, $I_{0}(\cdot)$ 为第一类 0 阶修正贝塞尔函数。定义 $K=\frac{c^{2}}{2 \sigma^{2}}$ , 表示主信号功率与多径分量功率之比, $\mathbf{K}=\mathbf{0}$ 时（即不存在视距分量), Rice分布等效为 Rayleigh分布。

2.频率选择性衰落

若信道时延 $\left|\tau_{i}(t)\right|_{\max }>T$ , 则 $\boldsymbol{b}\left(\boldsymbol{t}-\boldsymbol{\tau}_{\boldsymbol{i}}(\boldsymbol{t})\right)$ 不能近似为 $\boldsymbol{b}(\boldsymbol{t}-\overline{\boldsymbol{\tau}(\boldsymbol{t})})$ 。

干扰可存在于不同码元。

不同路径的不同信息码元之间会产生很大的相互干扰，称为码间干扰或者符号间千扰, 产生严重波形失真, 引起很大误码, 影响通信质量。

接收信号以及其信息信号的幅度和相位都将产生畸变; 频率域上看, 即不同频率分量受到不同程度的衰落, 称为频率选择性衰落。

绿色矩形代表码元，红色为信道：

分别为平坦与频率选择性衰落。

多径随参信道的时延扩展与相干带宽

此两参量阐明在什么条件下信号通过随参信道传输会引起平坦性或频率选择性衰落

随参信道的多径时延特性

均方根时延扩展 (时延扩展)：
$\sigma_{\tau}=\sqrt{\overline{\tau^{2}}-(\bar{\tau})^{2}}$
最大时延差: $\tau_{\max }$ 。

多径信道的频域特性

以二径信道模型为例: $\cos 2 \pi f t$ ,经过二径信道传输, 有 $\cos 2 \pi f t+A \cos 2 \pi f(t-\tau) =A \cos 2 \pi f t+A \cos (2 \pi f t+\phi), \phi=-2 \pi f \tau$ 。
两径矢量之和为向量 $\vec{B}$ , 信道输出 $r (t)$ 的幅度和相位与二径信号的相位差 $\phi=-2 \pi f \tau$ 有关; 若时延差 $\tau$ 为常数,则对不同频率 f, $\phi=-2 \pi f \tau$ 不同。

当 $\phi=0,2 \pi, 4 \pi, \ldots, r(t)$ 的幅度 $|\vec{B}|$ 最大为 $2 A$ , 当 $\boldsymbol{\phi}=\boldsymbol{\pi}, 3 \pi, 5 \pi \ldots$ , 幅度 $|\vec{B}|$ 最小为 “0.”

信道的传输特性: $H(f)=1+e^{-j 2 \pi f \tau}$ , 其幅频特性 $|H(f)|=2|\cos (\pi f \tau)|$ 。

时延差的倒数称为信道的相干带宽 $B_{c}=1 / \tau$ 。

若信号带宽 $B<B_{c}$ 信号通过信道失真可忽略; 若 $\geq B_{c}$ 信号通过信道失真很大。

对于多径信道, 可用时延扩展近似求出信道的相干带宽

$B_{c} \approx \frac{1}{\sigma_{\tau}}$

当信号带宽 $B>B_{c}$ , 信号遭受频率选择性衰落, 引起码间干扰; 当 $\ll B_{c}$ 时, 信号遭受平坦衰落。

移动信道的多普勒扩展及相干时间

1.多普勒扩展

移动通信中, 移动台与基站间的相对运动, 会使接收信号的载频发生多普勒频移。
对于频率为 $f_{c}$ 的单频信号, 受多普勒频移, 其频谱范围约为 $\left(f_{c}-f_{m}, f_{c}+f_{m}\right)$ 。其中 $f_{m}=\frac{v}{\lambda}=\frac{v f_{c}}{c}$ 为最大多普勒频移 (v 移动速度, $\lambda$ 载波波长, c 光速)。

设发射信号为频率是 $f_{c}$ 的正弦波, 到达移动台的路径与移动台运动方向夹角为 $\theta$ , 则多普勒频移 $f_{d}=f_{m} \cos \theta$ 。

图中X&Y 代表移动台。

2.信道的相干时间 Tc 和多普勒频率扩展

定义最大多普勒频移 $f_{m}$ 的倒数为信道的相干时间 $T_{c}$ , $T_{c}=1 / f_{m}$ 。它反映信道冲激响应对所传输的信号产生快衰或慢衰的影响。

定义最大多普勒频率 $B_{D}=f_{m}$ 为多普勒频率扩展。

3.多普勒扩展对衰落的影响

快衰落信道: $T_{s}>T_{c}$ 或信号的符号速率 $R_{s}<B_{D}$ , 即信道相干时间小于信号码元周期（符号间隔），因而在信号符号间隔时间内, 信道冲激响应快速变化, 使信号产生失真——快衰落信道或称为时间选择性衰落

慢衰落信道: $T_{s}<<T_{c}$ 或 $R_{s}>>B_{D}$ , 即信号码元周期（符号间隔）远小于信道相干时间，或信号符号速率远大于信道的多普勒频率扩展, 则信道冲激响应变化速率低于信号符号速率, 在信号符号间隔时间内信道冲激响应基本不变, 此时信号遭受慢衰落。