我觉得这句话说的很好:
kmp算法关键在于:在当前对文本串和模式串检索的过程中,若出现了不匹配,如何充分利用已经匹配的部分,来继续接下来的检索。
暴力解决字符串匹配
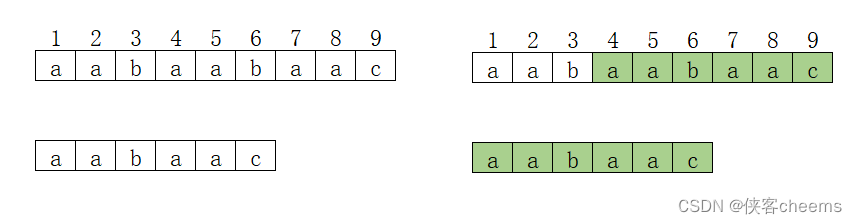
暴力解法就是两层for循环,每次都一对一的匹配,如果匹配错误就文本串开始位置加1,继续下一次
前缀表的作用
前缀表的作用就是当前位置匹配失败之后,通过前缀表记录的数字来去找到模式串中最合适的位置去重新开始下一次匹配,也就是说,匹配到当前位置失败,通过前缀表跳到前面位置继续匹配。
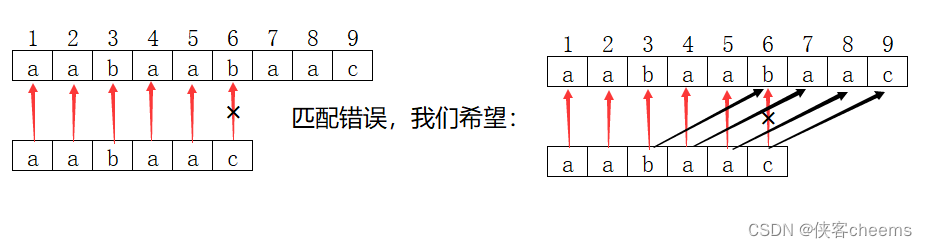
我们一个一个匹配,如果出现不匹配,这时候我们希望通过已经匹配过的字符串,找到其相同的前缀与后缀,来继续接下来的匹配。
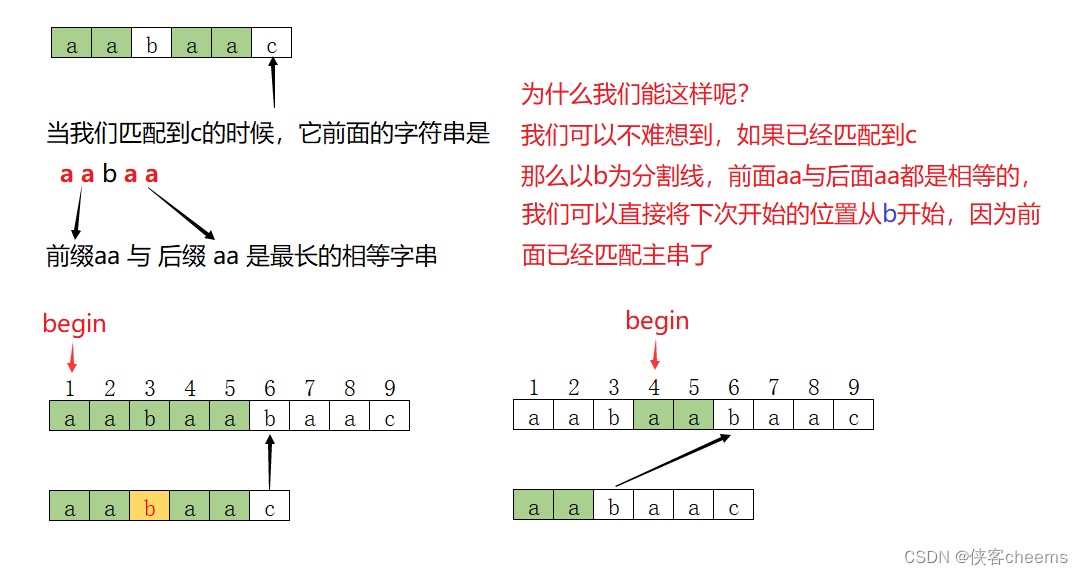
那我们该如何去计算这个前缀字串与后缀字串在每个位置的最大值,来去继续模式串匹配呢?就是接下来的前缀表的计算(也就是很多KMP算法中next数组的计算)
前缀表的计算(next数组计算)
- 什么是前缀?
前缀就是一个字符串不包括最末尾的字符从第一个开始的所有连续字串
主串:aabaac
前缀:a 、aa 、aab 、aaba 、aabaa - 什么是后缀?
后缀就是一个字符串不包含第一个字符,每次以末尾结尾的连续字串
主串:aabaac
后缀:c 、ac 、aac 、baac 、abaac - 如何计算前缀表?
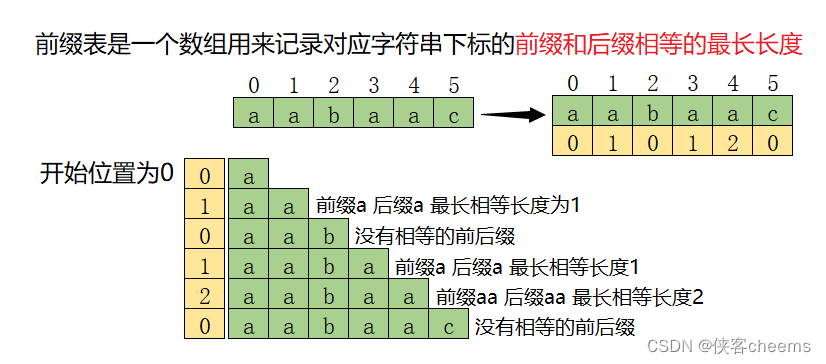
如何使用前缀表?
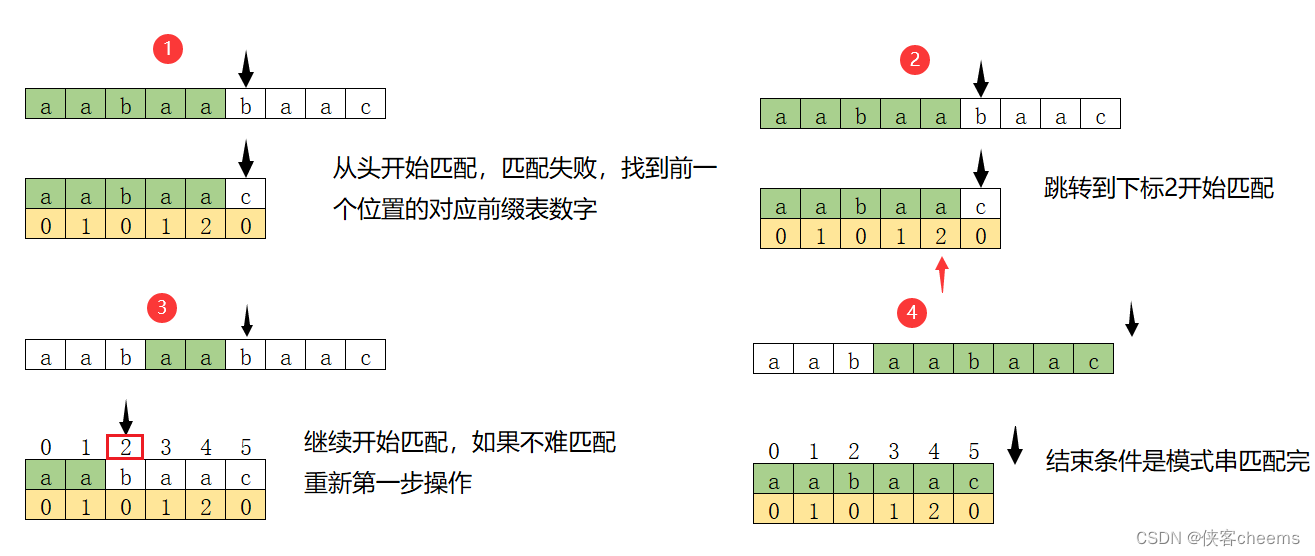
在KMP算法中,一般的next数组会直接使用前缀表,也可能在前缀表的基础上改进一点,但是最终的思路都是围绕前缀表展开,比如有些实现方法是把前缀表统一减一或者整体右移一位,初始位为-1。
时间复杂度:主串与模式串匹配过程最多为O(N),模式串的next数组生成为O(M),所以最后的时间复杂度可以为O(N+M),相较于暴力写法的O(N*M),KMP算法还是极大的提高了检索的效率。
本文主要是看了代码随想录的有感理解+画图🚀🚀