🚀 算法题 🚀

🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀
🌲 越难的东西,越要努力坚持，因为它具有很高的价值，算法就是这样✨
🌲 作者简介：硕风和炜，CSDN-Java领域新星创作者🏆，保研|国家奖学金|高中学习JAVA|大学完善JAVA开发技术栈|面试刷题|面经八股文|经验分享|好用的网站工具分享💎💎💎
🌲 恭喜你发现一枚宝藏博主,赶快收入囊中吧🌻
🌲 人生如棋，我愿为卒，行动虽慢，可谁曾见我后退一步？🎯🎯

🚀 算法题 🚀

🚗 知识回顾

大家再看这道题目之前，可以先去看一下我之前写过的一篇关于连续子数组算法题的博客，再看这个题目就更容易理解了。
博客的地址放到这里了，可以先去学习一下这到题目。

• 【LeetCode: 53. 最大子数组和 | 暴力递归=＞记忆化搜索=＞动态规划 | 分治法 】

🚩 题目链接

• 718. 最长重复子数组

⛲ 题目描述

给两个整数数组 nums1 和 nums2 ，返回 两个数组中 公共的 、长度最长的子数组的长度 。

示例 1：

输入：nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]
输出：3
解释：长度最长的公共子数组是 [3,2,1] 。
示例 2：

输入：nums1 = [0,0,0,0,0], nums2 = [0,0,0,0,0]
输出：5

提示：

1 <= nums1.length, nums2.length <= 1000
0 <= nums1[i], nums2[i] <= 100

🌟 求解思路&实现代码&运行结果

---

⚡ 暴力递归

🥦 求解思路

1. 子数组类型的题目我们同样可以从以某一位个位置结尾的情况是什么样的角度来进行一个思考。
2. 因为需要满足连续的性质，并且满足两个数组下标位置对应的元素相等，此时当前结果可能由前一个位置结果+1来到当前位置，还有可能就是以当前位置结尾的情况。
3. 那上述情况只能得到一种结果，我们需要找到所有nums1数组中可能以i位置结尾，并且nums2数组中可能以j位置结尾的所有可能的情况，枚举所有可能，找到最大值即可。
4. 下面就是代码的具体实现过程。

🥦 实现代码

class Solution {
    public int findLength(int[] nums1, int[] nums2) {
        int max=0;
        for(int i=0;i<nums1.length;i++){
            for(int j=0;j<nums2.length;j++){
                max=Math.max(max,process(i,nums1,j,nums2));
            }
        }
        return max;
    }

    public int process(int i,int[] nums1,int j,int[] nums2){
        if(i<0||j<0){
            return 0;
        }
        int max=0;
        if(nums1[i]==nums2[j]){
            max=Math.max(max,process(i-1,nums1,j-1,nums2)+1);
        }
        return max;
    }
}

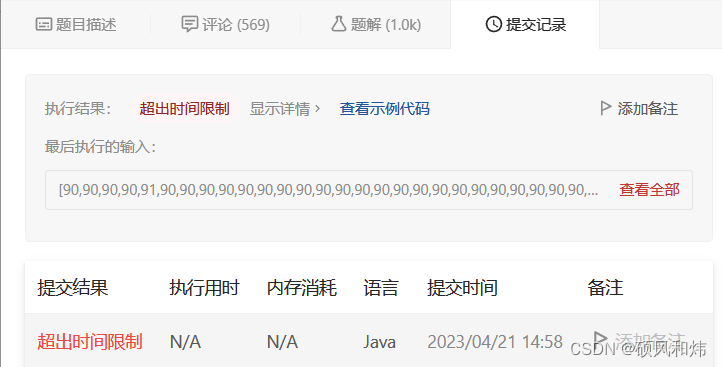
🥦 运行结果

时间超限了，不要紧哦，我还有锦囊妙计！

---

⚡ 记忆化搜索

🥦 求解思路

1. 根据我们递归的分析，在递归的过程中会产生重复的子过程，所以我们想到了加一个缓存表，也就是我们的记忆化搜索。

🥦 实现代码

class Solution {
    int[][] dp;
    public int findLength(int[] nums1, int[] nums2) {
        dp=new int[nums1.length][nums2.length];
        for(int i=0;i<nums1.length;i++) Arrays.fill(dp[i],-1);
        int max=0;
        for(int i=0;i<nums1.length;i++){
            for(int j=0;j<nums2.length;j++){
                max=Math.max(max,process(i,nums1,j,nums2));
            }
        }
        return max;
    }

    public int process(int i,int[] nums1,int j,int[] nums2){
        if(i<0||j<0){
            return 0;
        }
        if(dp[i][j]!=-1) return dp[i][j];
        int max=0;
        if(nums1[i]==nums2[j]){
            max=Math.max(max,process(i-1,nums1,j-1,nums2)+1);
        }
        return dp[i][j]=max;
    }
}

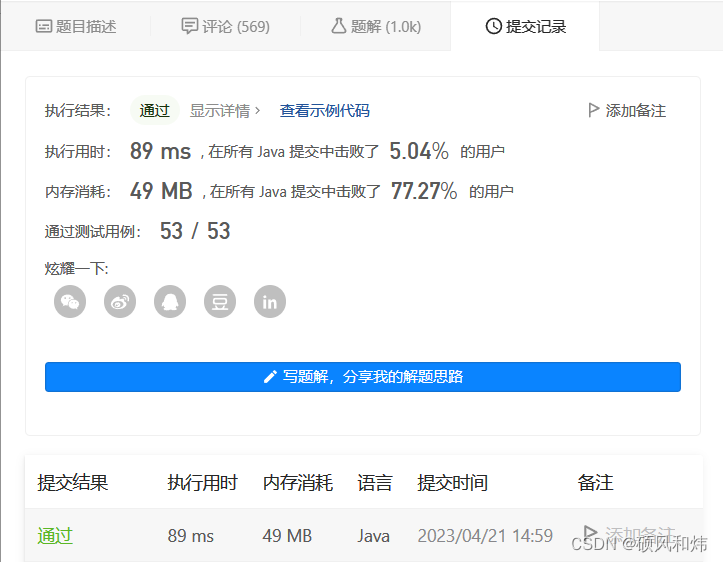
🥦 运行结果

---

⚡ 动态规划

🥦 求解思路

1. 按照我们之前递归和记忆化搜索的思路，通过动态规划实现出来。

🥦 实现代码

实现方式1

class Solution {
    int[][] dp;
    public int findLength(int[] nums1, int[] nums2) {
        dp=new int[nums1.length][nums2.length];
        int max=0;
        for(int i=0;i<nums1.length;i++){
            dp[i][0]=nums1[i]==nums2[0]?1:0;
            max=Math.max(dp[i][0],max);
        }
        for(int i=0;i<nums2.length;i++){
            dp[0][i]=nums1[0]==nums2[i]?1:0;
            max=Math.max(dp[0][i],max);
        }
        for(int i=1;i<nums1.length;i++){
            for(int j=1;j<nums2.length;j++){
                int res=0;
                if(nums1[i]==nums2[j]){
                    res=Math.max(res,dp[i-1][j-1]+1);
                }
                dp[i][j]=res;
                max=Math.max(max,dp[i][j]);
            }
        }
        return max;
    }
}

实现方式2

class Solution {
    int[][] dp;
    public int findLength(int[] nums1, int[] nums2) {
        dp=new int[nums1.length+1][nums2.length+1];
        int max=0;
        for(int i=nums1.length-1;i>=0;i--){
            for(int j=nums2.length-1;j>=0;j--){
                int res=0;
                if(nums1[i]==nums2[j]){
                    res=Math.max(res,dp[i+1][j+1]+1);
                }
                dp[i][j]=res;
                max=Math.max(max,dp[i][j]);
            }
        }
        return max;
    }
}

🥦 运行结果

---

🍖 课后加餐

下面这道题目的求解思路和该题有异曲同工之妙，感兴趣的同学赶快试试吧！

• 674. 最长连续递增序列

💬 共勉

最后，我想和大家分享一句一直激励我的座右铭，希望可以与大家共勉！