学习目标:
学习插值的基础理论可以从以下几个方面入手:
-
理解插值的概念:插值是指根据已知数据点的函数值,构造出经过这些点的函数,用于在已知数据点之间估计函数值。可以将其看做是一种函数逼近的方法。
-
掌握插值多项式:插值的核心是构造插值多项式,即通过已知数据点,构造出经过这些点的一个多项式。常用的插值多项式包括拉格朗日插值多项式和牛顿插值多项式。
-
学习插值误差的估计:在进行插值时,需要评估插值的准确度,也就是估计插值误差。了解误差估计的方法,可以帮助选择合适的插值方法,提高插值的准确度。
-
掌握插值方法的优缺点:不同的插值方法有不同的优缺点,比如拉格朗日插值多项式容易求解但是误差较大,而样条插值方法可以更好地平滑插值函数但是计算量较大。了解各个插值方法的优缺点,可以根据实际情况选择合适的方法。
-
实践应用:在掌握了插值的基础理论后,需要通过实践应用来进一步巩固和加深理解。可以通过使用Python、MATLAB等数学软件进行插值函数的构造和绘制,或者利用已有的数据进行实际应用,比如图像处理、数据拟合等。

为什么有插值:
插值是为了解决实际问题中需要用到函数但函数并未提供所需点的取值的情况。例如,当我们需要在某些离散数据点之间求解函数值时,我们可以使用插值方法来近似得到这些离散点之间的函数值。在实际应用中,这种情况非常常见,因为很多实验数据只提供了有限的离散数据点,而需要对这些数据进行分析和处理,就需要使用插值方法得到函数值。

4.1.1 插值问题的提法
插值问题的一般提法是:已知一组数据点$(x_0,y_0),(x_1,y_1),\cdots,(x_n,y_n)$,要求构造一个函数$f(x)$,使得$f(x_i)=y_i$,其中$i=0,1,\cdots,n$。
在插值问题中,常常要求插值函数通过所有给定数据点,这称为“完全插值”问题。如果只要求插值函数在数据点处与数据点函数值相等,但并不一定要求插值函数经过所有数据点,则称为“部分插值”问题。
我的理解:
插值问题的提法可以这样理解:我们有一些已知的数据点,需要通过这些数据点来构造一个函数$f(x)$,使得这个函数在这些数据点上的函数值与给定的数据点上的函数值相等,即满足$f(x_i) = y_i$,其中$(x_i, y_i)$为给定的数据点。如果这个函数在这些数据点上不仅满足函数值相等的条件,还满足通过这些数据点,即在这些点上有一定的连续性和光滑性,就称之为插值函数。
在实际应用中,我们往往需要用到一些离散的数据点,并且需要对这些数据进行分析和处理。插值问题就是针对这种情况的一种解决方法,它可以通过已知的数据点来构造一个函数,从而得到在数据点之间的函数值。这种方法在各种科学和工程领域都有广泛的应用,例如在数值分析、数值计算、统计学、物理学、工程学等领域中都有着重要的应用。

4.1.2 插值多项式的存在唯一性
插值多项式在满足一定条件下是唯一的。具体来说,如果给定 n+1个不同的点 (x_0,y_0), (x_1,y_1),\cdots,(x_n,y_n),且 f(x)是在这些点上的一个次数不超过 n 的多项式,那么这个多项式就是唯一的。
该定理的证明可以用反证法来完成。假设存在两个次数不超过 $n$ 的多项式 p(x) 和 q(x),它们在给定的 n+1个点上取值相同,即 p(x_i)=q(x_i)=y_i, i=0,1,\cdots,n。我们可以构造另一个多项式 r(x)=p(x)-q(x),它的次数也不超过 n。由于p(x) 和 q(x) 在给定的点上的取值相同,因此 r(x) 在这些点上的取值为 0。这意味着 r(x)至少有 n+1个根,而由于 r(x)的次数不超过 n,因此它最多只有 $n$ 个根,这就导致了矛盾。因此,假设不成立,插值多项式是唯一的。
需要注意的是,在实际应用中,插值多项式的唯一性只是理论上的概念,由于计算机舍入误差等原因,使用不同的计算方法可能得到略有不同的插值多项式。
我的理解:
插值多项式的唯一性指的是,在给定的插值节点下,一个函数的插值多项式是唯一的。
具体来说,给定一组插值节点 x_0, x_1, \ldots, x_n,假设存在两个 n 次多项式 p(x)和 q(x),它们在这些节点上的函数值相同,即 $p(x_i) = q(x_i)$,$i=0,1,\ldots,n$。那么,p(x) 和 q(x)在整个区间 [x_0, x_n]上的函数值也是相等的,即 p(x) = q(x),x \in [x_0, x_n]。
因此,对于给定的插值节点,插值多项式的系数是唯一的,可以用不同的方法求解,如拉格朗日插值、牛顿插值等。
4.1.3 插值余项
插值余项是用来描述插值多项式与原函数之间的误差的概念。它表示在用插值多项式 P_n(x)逼近函数 f(x) 时,f(x)和 P_n(x)之间的差距,即:
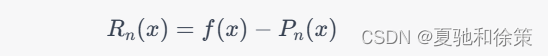
其中,P_n(x) 是 n次插值多项式,f(x)是待逼近的函数。
插值余项的求解方法通常有两种。一种是基于插值多项式的构造方法,比如拉格朗日插值和牛顿插值。另一种是基于误差估计的方法,比如利用插值余项的导数或者高次导数的上界来进行估计。
插值余项的概念对于评估插值多项式的逼近效果非常重要。通过对余项的分析,我们可以得出很多有关插值多项式逼近效果的结论,比如插值多项式的收敛性、精度等等。同时,插值余项的概念也为设计更高效的插值算法提供了思路。
我的理解:
在插值问题中,插值多项式可能无法完美地拟合原函数。因此,我们需要一种方式来量化插值多项式的逼近程度,这就是插值余项。插值余项表示原函数与插值多项式之间的差异。
具体来说,给定一个函数 f(x),和一个在点集 x_0,x_1,\dots,x_n 处取值的插值多项式 p_n(x)$,则插值余项 $R_n(x)$ 定义为 $f(x)$ 减去插值多项式 $p_n(x)$ 的值,即

插值余项可以用来衡量插值多项式的精度,并且在实际应用中也有很大的作用。例如,在数值微积分中,我们可以使用插值多项式来估计原函数在某个区间上的积分,而插值余项则告诉我们估计值与真实值之间的误差大小。
总结:
插值是数值分析中重要的概念之一,主要用于根据已知数据点构造一个函数,使得该函数在这些数据点上与给定函数或数据完全一致或者足够接近。插值的重点和难点和易错点如下:
重点:
- 插值多项式的唯一性:给定一组数据点,对于一次或更高次的插值多项式,是否存在唯一的解,或者说该解是否唯一?
- 插值多项式的存在性:对于一组数据点,是否存在一个次数不超过给定值的插值多项式?
- 插值多项式的构造:如何构造插值多项式,通常采用的是拉格朗日插值或牛顿插值方法?
- 插值误差的估计:如何估计插值多项式的误差,通常采用的是拉格朗日余项或牛顿余项公式?
- 多项式插值的局限性:多项式插值在实际应用中具有一定的局限性,例如运用在高维数据的插值计算中存在维度灾难等问题。
难点:
- 插值多项式的误差分析:如何准确地估计插值多项式的误差,需要掌握一定的数学知识和技巧,例如导数的计算和上确界的估计等。
- 非等距节点的插值:对于一组非等距节点的数据点,如何进行插值计算,需要掌握一定的数值计算方法,例如切比雪夫节点、极大点和小极点等。
- 多项式插值的数值稳定性:多项式插值的计算涉及到对矩阵求逆或者进行高斯消元等操作,这些操作在数值上可能不够稳定,需要注意误差的累积问题。
易错点:
- 数据点的选择:插值多项式的构造与所选取的数据点密切相关,需要注意数据点的选择和分布情况,避免出现奇异点或者过拟合等问题。
- 插值多项式的次数:插值多项式的次数一般不能超过数据点数减1,否则可能出现龙格现象,需要控制多项式的次数。
- 插值误差的计算:插值误差的计算需要注意余项的计算和误差上界的估计,需要严格掌握公式和方法。