转化为01背包

题目链接:acwing4. 多重背包问题 I
题目描述
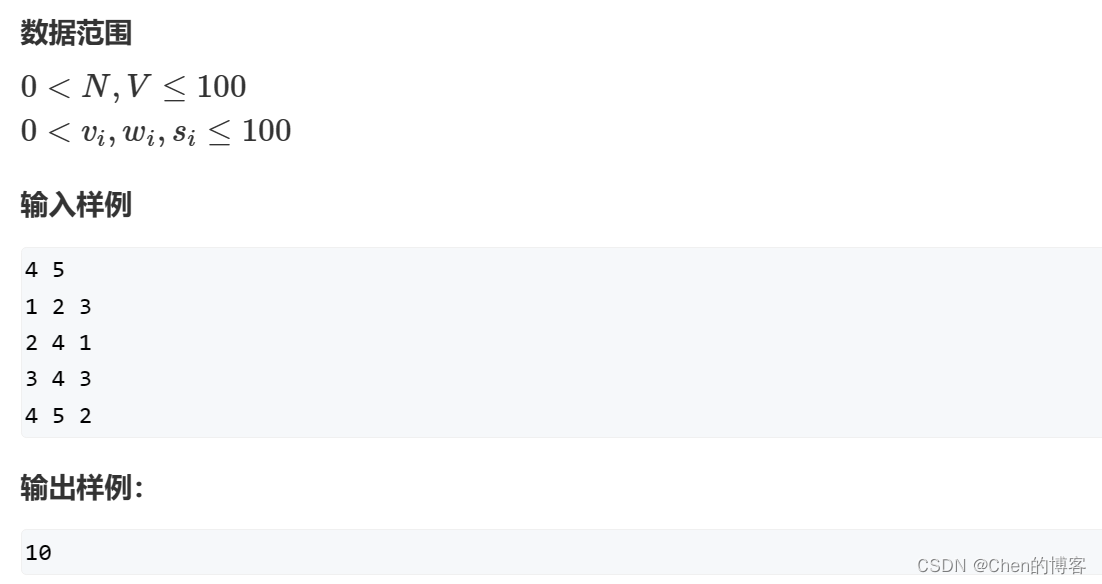
在这里插入图片描述
数据范围

思路：
可以转化为01背包问题求解，将s个物品都看作单独的一个物品，时间复杂度为 $O (N * V * S)$
代码如下：

#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<vector>
using namespace std;
typedef pair<int ,int> pii;
const int N=110;

int f[N];

int main(){
    int n,m;
    vector<pii> vv;
    cin>>n>>m;
    for(int i=0;i<n;i++){
        int v,w,s;
        scanf("%d%d%d",&v,&w,&s);
        for(int j=0;j<s;j++) vv.push_back({v,w});
            
    }
    for(int i=0;i<vv.size();i++)
        for(int j=m;j>=vv[i].first;j--)
            f[j]=max(f[j],f[j-vv[i].first]+vv[i].second);
    cout<<f[m];
    return 0;
}

二进制拆分优化

题目链接:acwing5. 多重背包问题 II
数据范围变大：
在这里插入图片描述
这时直接拆分为s份，转化为01背包问题求解会超时，考虑二进制拆分，二进制拆分参考博客
主要思路还是将其转化为01背包问题来求解，但是我们不必要将s个物品给看成s个单独的物品，举个例子，二进制拆分是这样的：

10=1+2+4+3=2^0 + 2^1 + 2^2 + (10-2^0 + 2^1 + 2^2)
1~10中的每一个数都可以由1、2、4、3这四个数来表示出来，这样我们就不需要将s个物品拆分为s个单独的物品了。

时间复杂度为 $O (N * V * l o g (s))$
代码如下:

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
typedef long long ll;
typedef pair<ll,ll> pii;
const int N=2e3+10;

ll f[N];

int main(){
    int n,m;
    vector<pii> vv;
    cin>>n>>m;
    for(int i=0;i<n;i++){
        int v,w,s;
        scanf("%d%d%d",&v,&w,&s);
        for(int t=1;t<=s;t*=2){
            vv.push_back({(ll)t*v,(ll)t*w});
            s-=t;
        }
        if(s) vv.push_back({(ll)s*v,(ll)s*w});
    }
    
    for(int i=0;i<vv.size();i++)
        for(int j=m;j>=vv[i].first;j--) f[j]=max(f[j],f[j-vv[i].first]+vv[i].second);
    cout<<f[m];
    return 0;
}

单调队列优化

数据范围继续变大
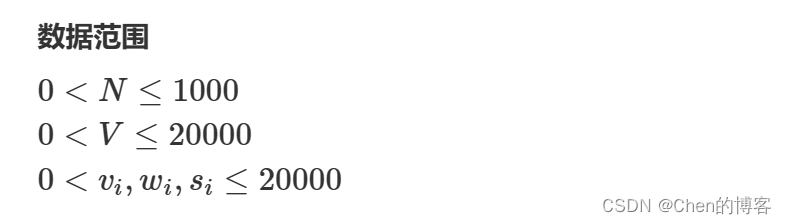
在这里插入图片描述
这里考虑用单调队列优化，首先分析01背包与完全背包，进而推导出多重背包的单调队列优化。

01背包:
用f[i][j]来表示考虑前i个物品，当前背包容量为j时的能装的最大价值
选或者不选物品i
f[i][j]=max(f[i-1][j],f[i-1][j-v]+w)
由于f[i]这一层只与上一层f[i-1]有关，所以我们考虑优化空间为一维
f[j]=max(f[j],f[j-v]+w)//等号左边的f[j]表示的是f[i][j],等式右边的f[j]表示的是f[i-1][j]
需要注意的地方是,如果我们从小到大遍历j的话，那么等式右边的f[j-v]表示的是f[i][j-v]
所以，我们需要从大到小枚举体积j

也就是：
for(int j=m;j>=v;j--) //v ,m为第i个物品的体积和价值
	f[j]=max(f[j],f[j-v]+w)

完全背包问题:
考虑选多少个物品i最好:(s为最多装多少个物品i,这点与多重背包不同，需要注意)
f[i][j]  =max(f[i-1][j],f[i-1][j-v]+w,f[i-1][j-2*v]+2*w,....,,f[i-1][j-s*v]+s*w)
可以发现:
f[i][j-v]=max(f[i-1][j-v]+w,f[i-1][j-2*v]+2*w,....,,f[i-1][j-s*v]+s*w)
观察上面可以得出:
f[i][j]=max(f[i-1][j],f[i][j-v]);
考虑对空间优化:
f[j]=max(f[j],f[j-v]);
这里遍历体积是从小到大遍历的,因为我们要的就是让等式左边的f[j-v]表示的是f[i][j-v]而不是f[i-1][j-v]

也就是:
for(int j=v;j<=m;j++) 
	f[j]=max(f[j],f[j-v]+w)

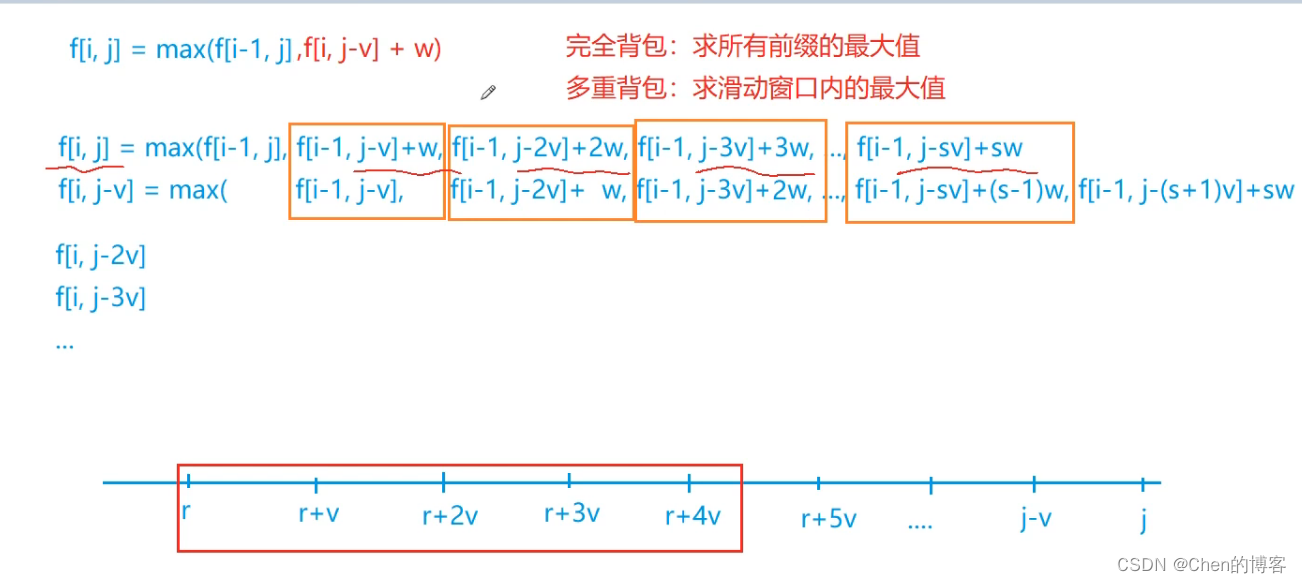
多重背包问题:
看懂了上面两步，我们可以来进行多重背包问题的推导
考虑物品i的个数为s，也就是最多被选s次

考虑选多少个物品i最好(<=s):
f[i][j]    =max(f[i-1][j],f[i-1][j-v]+w,f[i-1][j-2*v]+2*w,....,f[i-1][j-s*v]+s*w)
f[i][j-v]  =max(         f[i-1][j-v],f[i-1][j-2*v]+w,....,f[i-1][j-s*v]+(s-1)*w,f[i-1][j-(s+1)v]+sw)//注意这个地方的区别,最多选s个
f[i][j-2*v]=max(         f[i-1][j-2*v],f[i-1][j-3*v]+w,....,f[i-1][j-s*v]+(s-2)*w,f[i-1][j-(s+1)v]+(s-1)w,f[i-1][j-(s+2)*v]+s*w)//注意这个地方的区别,最多选s个
我们可以观察到,f[i][j-v]比f[i][j-2*v]多了一项f[i-1][j-v],少了一项f[i-1][j-(s+2)*v],
f[i][j]与f[i][j-v]的关系也是类似,这里我们可以想到学过的数据结构——单调队列,这样可以快速求出max,不过需要注意的是，按照加入队列的顺序不同，要加入不同的w，需要维持一个等差的关系开判断是否入队出队。

在这里插入图片描述

时间复杂度为 $O (N * M)$
代码如下:

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=20010;

int f[N];
int g[N],q[N];
int main(){
    int n,m;
    cin>>n>>m;
    for(int i=0;i<n;i++){
        int v,w,s;
        scanf("%d%d%d",&v,&w,&s);
        memcpy(g,f,sizeof f);
        for(int j=0;j<v;j++){
            int hh=0,tt=-1;
            for(int k=j;k<=m;k+=v){
                if(tt>=hh&&k-s*v>q[hh]) hh++;//队尾出队
                if(tt>=hh) f[k]=max(g[k],g[q[hh]]+(k-q[hh])/v*w);//求出在队尾的最大值
                while(hh<=tt&&g[k]>=g[q[tt]]+(k-q[tt])/v*w) tt--;//维护单调队列
                q[++tt]=k;//入队
            }
        }
    }
    cout<<f[m]<<endl;
    return 0;
}