基于动态车辆模型的百度Apollo LQR和MPC横向控制算法分析（Matlab代码实现）

news2024/11/20 4:53:29

💥1 概述

📚2 运行结果

🎉3 参考文献

👨‍💻4 Matlab代码

💥1 概述

Apollo 是由百度发起的一个高效、灵活的基于自动驾驶的测试和研发的平台。Apollo 的主要逻辑为局部规划 +轨道跟踪。在局部规划时，由低精度模型 + 长周期规划组成。在跟踪控制层面上是有高精度模型 + 短周期规划组

成。本文主要是对于 Apollo 控制算法中的 MPC（模型预测控制）和 LQR（线性二次调节器）这两种路径跟踪控制器进行分析与比较。

MPC（模型预测控制）是一种先进的过程控制方法，在满足一定约束条件的前提下，用于实现控制的过程。他的实现依赖于过程的动态线性模型。在控制时域内，MPC 将主要对当前时刻进行优化，但同时也会考虑未来时刻，求

取当前时刻的最优解，然后反复优化，从而实现在整个时域内的优化求解。

LQR（线性二次调节器）是现代控制理论中发展十分成熟的一种状态空间设计方法。LQR 算法可得到状态线性反馈的最优控制规律，易于形成闭环最优控制。LQR 的最优设计是指设计出的状态反馈器 K 要使二次型目标函数J 取最小值，而 K 有权矩阵 Q 与 R 唯一决定，在汽车不同的速度下，Q 与 R 的不同会对算法的效果有着重要的影响，所以 Q，R 的选值十分重要。

MPC 的研究对象是以现代控制理论中的以状态空间方程的形式给出的线性系统。对于 MPC 控制器，他的研究对象既可以是线性系统，也可以是非线性系统。LQR 的研究对象是以状态空间方程形式给出的线性系统。然而由于对效率和时耗的考虑，通常会将非线性系统线性化进行计算。

在 Apollo 算法中，LQR 和 MPC 都选用单车动力学模型作为研究对象。单车系统为非线性系统，但 LQR 和MPC 控制器的目的是为了求最优控制解，在优化过程中都会将其线性化，所以也可以说 Apollo 中研究的对象都为线性系统。

📚2 运行结果

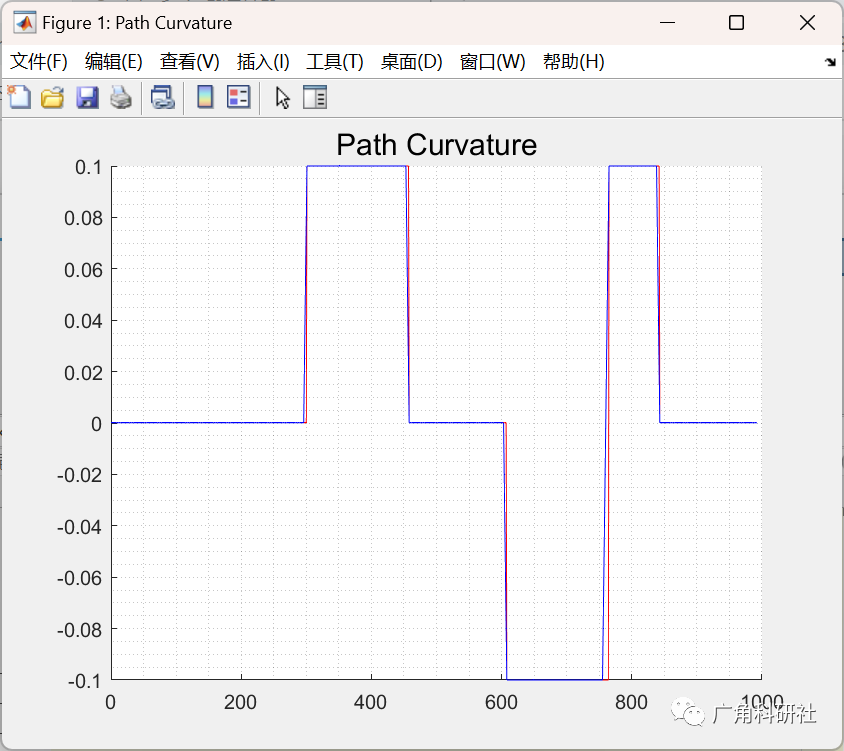
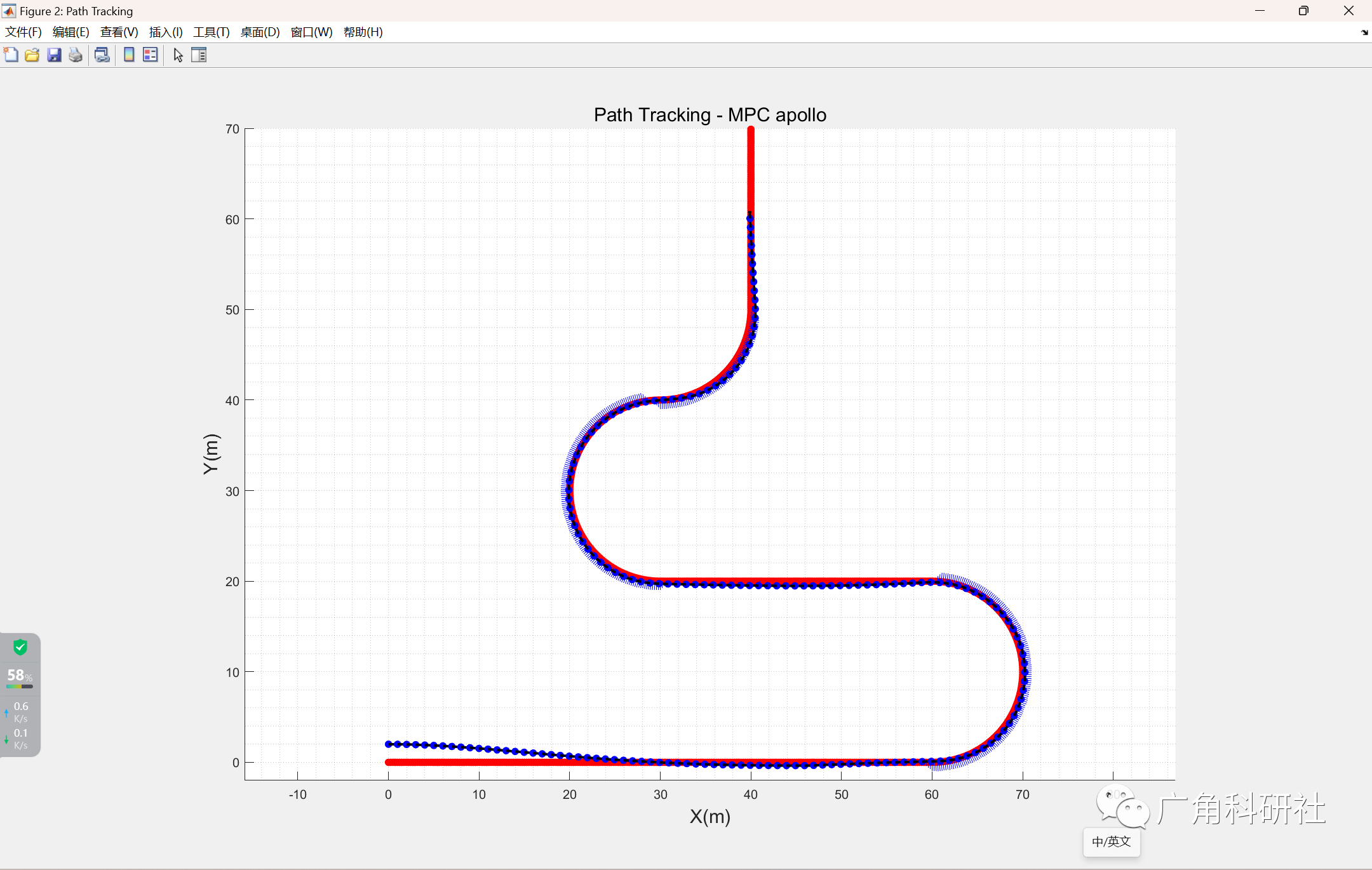
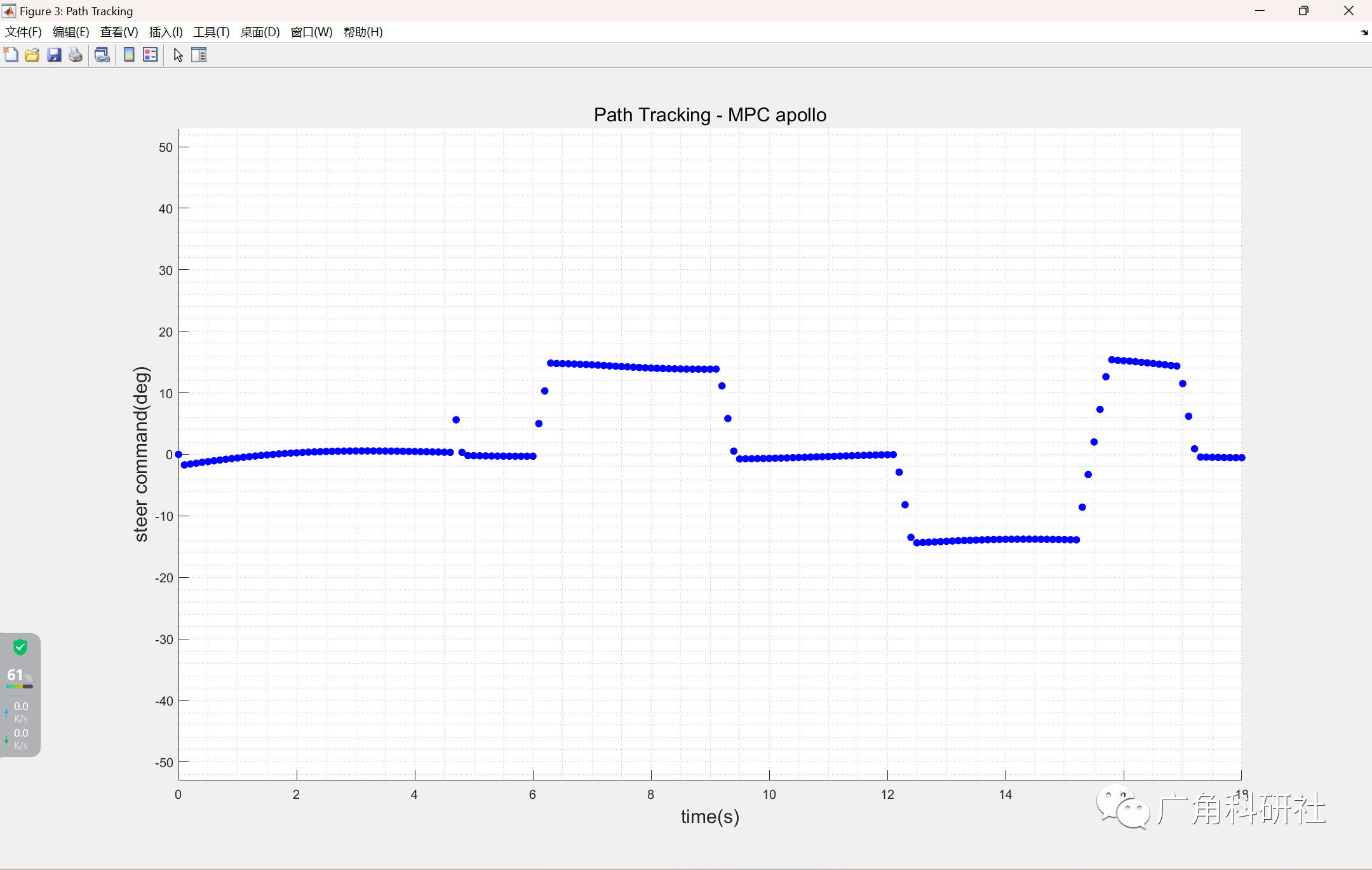
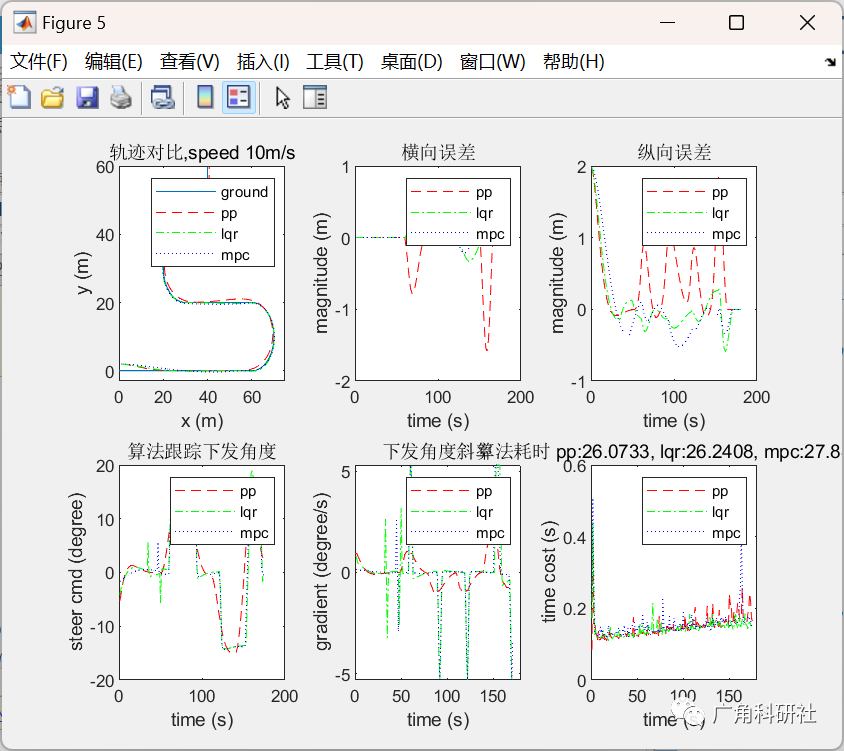
主函数部分代码：

clc; clear; close all;
rng('default');

% Ankush Chakrabarty (chakank@me.com)

%% Control surface regression

% Loading controller samples (within feasible region)
load('samples_for_ENMPC.mat', 'Xf', 'Uf', 'svm')
;
S = @(x,y) [1, x, y, x*y, (2*x^2-1)*y, (2*y^2-1)*x,...
            (4*x^3 - 3*x), (4*y^3 - 3*y)];

for k = 1:size(Xf,1)
    G(k,:) = S(Xf(k,1), Xf(k,2));
end

c = G\Uf;
fprintf('\nDisplaying coefficients of the controller...\n');
disp(table(c));

fprintf('\nDisplaying basis functions...\n');
disp(S);

%% Testing closed-loop control
T = 10;      % time of simulation
load('dataset.mat', 'MPC')
;
% Choosing an initial state that is feasible
start_feasible = 0;
while start_feasible == 0
    x0 = MPC.Xlb + rand(2,1)*(MPC.Xub - MPC.Xlb);
    start_feasible = predict(svm, x0(:).') > 0.1;
end

% Running Simulink file
fprintf('\nRunning Simulink file...')
;figure(1);
sim('simulation_ENMPC.slx');
tx = xhist.Time.';
x = xhist.Data.';

%% Plotting
subplot(2,1,1)
;plot(tx, x([1,2],:).', 'linewidth', 2);
h = legend('x_1', 'x_2');
set(h, 'orientation', 'horizontal');
set(gca, 'fontsize', 20);
xlabel('t');
ylabel('x(t)');
hold on
subplot(2,1,2)
;tu = uhist.Time;
u = squeeze(uhist.Data);
plot(tu, u, 'linewidth', 2);
set(h, 'orientation', 'horizontal');
set(gca, 'fontsize', 20);
xlabel('t');
ylabel('u(t)');
hold on