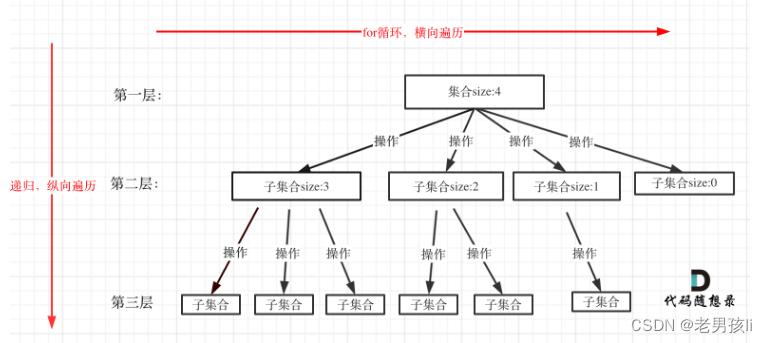
#回溯模板,伪代码
def backtracking(参数):
if (终止条件):
存放结果
return #如果要将数层中间的结果也插入,就不用写return,比如子集问题
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)):
处理节点
backtracking(参数) // 递归
回溯,撤销处理结果
在类中实现回溯方法时,可以将回溯方法放在别的方法中,也可以将回溯方法单独写出来,如下
例题1:(出自代码随想录回溯算法中的2(组合问题),力扣上77题)
给定两个整数 n 和 k,返回 1 ... n 中所有可能的 k 个数的组合。可以按 任何顺序 返回答案。
示例: 输入: n = 4, k = 2 输出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]
#方法一:回溯方法写在其他方法内,回溯中的参数不用加self
class Solution:
def combine(self, n: int, k: int) :
result = []
path = []
def backtracking(n,k,start):
if len(path) == k:
result.append(path[:])
return
for i in range(start,n + 1):
path.append(i)
backtracking(n,k,i + 1)
path.pop()
backtracking(n,k,1)
return result
#方法二:回溯方法单独写,回溯中的参数需要加self
class Solution:
def __init__(self):
self.result = []
self.path = []
def backtracking(self,n,k,start):
if len(self.path) == k:
self.result.append(self.path[:])
return
for i in range(start,n + 1):
self.path.append(i)
self.backtracking(n,k,i + 1)
self.path.pop()
def combine(self, n: int, k: int):
self.backtracking(n,k,1)
return self.result例题2:回溯法去重,防止结果中出现重复的集合(回溯算法第8题:组合总和ll)
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
- 示例 1:
- 输入: candidates = [10,1,2,7,6,1,5], target = 8,
- 所求解集为:
[
[1, 7],
[1, 2, 5],
[2, 6],
[1, 1, 6]
]思路:首先对candidates排序,在回溯时要去重,同一层不能有重复的元素
class Solution:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
result = []
path = []
def backtrack(candidates,target,sum_,start):
if sum_ == target:
result.append(path[:])
return
elif sum_ > target: return
for i in range(start,len(candidates)):
if i > start and candidates[i] == candidates[i - 1]:
continue
#此两句为去重核心,尤其是i>start说明这一层已经开始循环了
if candidates[i] > target - sum_: return
path.append(candidates[i])
sum_ += candidates[i]
backtrack(candidates,target,sum_,i + 1)
a = path.pop()
sum_ -= a
candidates.sort()
backtrack(candidates,target,0,0)
return result另一种同一数层去重:例题:回溯算法14-递增子序列
数层,树枝双去重:例题:回溯算法16-全排列ll