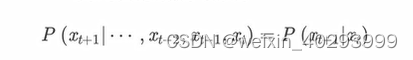本篇介绍第一个机器学习算法:k-近邻算法,它非常有效而且易于掌握。首先,我们将探讨k-近邻算法(KNN)的基本理论,以及如何使用距离测量的方法分类物品;其次我们将使用Python从文本文件中导入并解析数据;再次,本书讨论了当存在许多数据来源时,如何避免计算距离时可能碰到的一些常见错误;最后,利用实际的例子讲解如何使用k-近邻算法改进约会网站。
概念:简单地说,k-近邻算法采用测量不同特征值之间的距离方法进行分类。
优点:精度高、对异常值不敏感、无数据输入假定
缺点:计算复杂度高、空间复杂度高;
必须要有接近实际数据的训练样本数据,所以必须保存全部数据集,若训练数据集很大则需要使用大量的存储空间。由于又必须对数据集中的每个数据计算距离值,实际使用时可能会非常耗时(优化实现:kd树)。
适用数据范围:数值型和标称型
工作原理:存在一个样本数据集合,也称作训练样本集,并且样本集中每个数据都存在标签,即我们知道样本集中每一数据与所属分类的对应关系。输入没有标签的新数据后,将新数据的每个特征与样本集中数据对应的特征进行比较,然后算法提取样本集中特征最相似数据(最近邻)的分类标签。一般我们只选择样本数据集中前k个最相似的数据,这就是k-近邻算法中k的出处,通常k是不大于20的整数。最后,选择k个最相似数据中出现次数最多的分类,作为新数据的分类。
k值的选择:交叉验证法
Kd树构造算法:给定一个目标点,搜索其最近邻。首先找到包含目标点的叶结点;然后从该叶结点出发,依次回退到父结点:不断查找与目标点最邻近的结点,当确定不可能存在更近的结点时终止。这样搜索就被限制在空间的局部区域上,效率大为提高。


案例(电影分类):首先计算未知电影与样本集中其他电影的距离,如表2-2所示。此处暂时不要关心如何计算得到这些距离值,使用Python实现电影分类应用时,会提供具体的计算方法。

现在我们得到了样本集中所有电影与未知电影的距离,按照距离递增排序,可以找到k个距离最近的电影。假定k=3,则三个最靠近的电影依次是He’s Not Really into Dudes、 Beautiful Woman和California Man。 k-近邻算法按照距离最近的三部电影的类型,决定未知电影的类型,而这三部电影全是爱情片,因此我们判定未知电影是爱情片。
伪代码:
对未知类别属性的数据集中的每个点依次执行以下操作:
(1) 计算已知类别数据集中的点与当前点之间的距离;
(2) 按照距离递增次序排序;
(3) 选取与当前点距离最小的k个点;
(4) 确定前k个点所在类别的出现频率;
(5) 返回前k个点出现频率最高的类别作为当前点的预测分类。
Python3实现完整代码:
import pandas as pd
from numpy import *
import operator
import numpy as np
def knn_classify(inX, data_set, labels, k): # KNN算法实现
data_set_size = data_set.shape[0]
# 计算欧式距离
diffMat = tile(inX, (data_set_size, 1)) - data_set # 距离矩阵
sqDiffMat = diffMat ** 2
sqDistances = sqDiffMat.sum(axis=1)
distances = sqDistances ** 0.5
# 距离从小到大排序
sortedDistIndicies = distances.argsort()
# 获取前k个距离最小元素所在分类,计算各分类发生频率
class_count = {}
for i in range(k):
voteIlabel = labels[sortedDistIndicies[i]]
class_count[voteIlabel] = class_count.get(voteIlabel, 0) + 1
# 发生频率从大到小排序
sorted_class_count = sorted(class_count.items(), key=operator.itemgetter(1), reverse=True)
return sorted_class_count[0][0] # 返回频率最高的标签作为最终分类
if __name__ == '__main__':
# 1、准备数据
group = np.array([[1.0, 1.1], [1.0, 1.0], [0, 0], [0, 0.1]])
labels = ['A', 'A', 'B', 'B']
import matplotlib.pyplot as plt
plt.scatter([g[0] for g in group], [g[1] for g in group], marker='.', color='black', s=20)
for i in range(group.shape[0]):
plt.text(group[i][0], group[i][1], labels[i]) # 加标签
plt.show()
# 2、KNN算法实现
k = 3
knn_classify([0, 0], group, labels, k)
# 3、算法测试(以相亲约会数据为例)
data = pd.read_table("E:\datingTestSet.txt", header=None, sep="\t")
data.columns = ["里程数/年", "游戏时间占比", "冰淇淋公升数/周", "匹配类型"]
datingDataMat = data[["里程数/年", "游戏时间占比", "冰淇淋公升数/周"]].to_numpy()
datingLabels = data[["匹配类型"]].to_numpy()
datingLabels = [d[0] for d in datingLabels] # 去列表并数值化
datingLabels = [1 if d == 'didntLike' else d for d in datingLabels]
datingLabels = [2 if d == 'smallDoses' else d for d in datingLabels]
datingLabels = [3 if d == 'largeDoses' else d for d in datingLabels]
# 3-1、画图统计描述
import matplotlib.pyplot as plt
# 游戏时间占比和冰淇淋公升数
plt.scatter(datingDataMat[:, 1], datingDataMat[:, 2], 15 * np.array(datingLabels), 15 * np.array(datingLabels))
plt.show()
# 里程数和游戏时间占比
plt.scatter(datingDataMat[:, 0], datingDataMat[:, 1], 15 * np.array(datingLabels), 15 * np.array(datingLabels))
plt.show()
# 3-2、数值归一化
minVals = datingDataMat.min(0)
maxVals = datingDataMat.max(0)
ranges = maxVals - minVals
m = datingDataMat.shape[0] # 行数
norm_data_set = datingDataMat - np.tile(minVals, (m, 1)) # tile是将minVals的行重复m次,列重复1次
norm_data_set = norm_data_set / np.tile(ranges, (m, 1))
# 3-3、测试验证
hoRatio = 0.10 # hold out 10%
m = norm_data_set.shape[0]
numTestVecs = int(m * hoRatio) # 验证集数量
errorCount = 0.0
for i in range(numTestVecs):
classifierResult = knn_classify(norm_data_set[i, :], norm_data_set[numTestVecs:m, :], datingLabels[numTestVecs:m], 3)
print("the classifier came back with: %d, the real answer is: %d" % (classifierResult, datingLabels[i]))
if classifierResult != datingLabels[i]:
errorCount += 1.0
print("error count: ", errorCount)
print("the total error rate is: %f" % (errorCount / float(numTestVecs)))
# 4、算法使用
result_list = ['not at all', 'in small doses', 'in large doses']
ff_miles = float(input("frequent flier miles earned per year?"))
percent_tats = float(input("percentage of time spent playing video games?"))
ice_cream = float(input("liters of ice cream consumed per year?"))
in_array = np.array([ff_miles, percent_tats, ice_cream])
classifier_result = knn_classify((in_array-minVals) / ranges, norm_data_set, datingLabels, 3)
print("You will probably like this person: ", result_list[classifier_result-1])
备注:
datingTestSet数据集直接去源码地址下载www.manning.com/MachineLearninginAction