它来了它来了!我们最爱的股票问题它来了!!
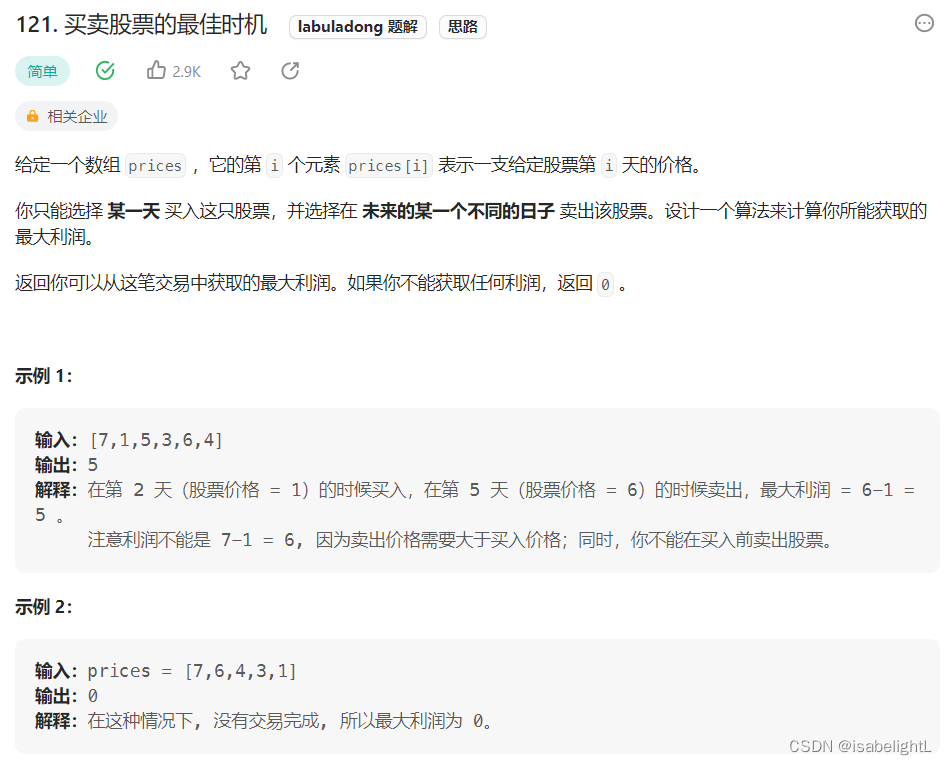
121. 买卖股票的最佳时机
链接:代码随想录
视频链接:动态规划之 LeetCode:121.买卖股票的最佳时机1_哔哩哔哩_bilibili
好难懂,尤其是理解状态的变化以及为什么要这么设置,花了大概一个半小时去理解什么叫”持有股票“,什么叫”不持有股票“。我自己拆分了下几种情况。
重点:
1、初始值不好理解
第0天(在买的情况下)能持有的最大资产
dp[0][0]=-prices[i]
第0天(在卖的情况下)能持有的最大资产,//第一天不能既买又卖,最大值为0
dp[0][1]=0我与他人的bettle结果
2、dp[i][1]的状态变化用到dp[i-1][0],因为这种情况下是第i天卖出,则前提条件是前面已经买入股票了。
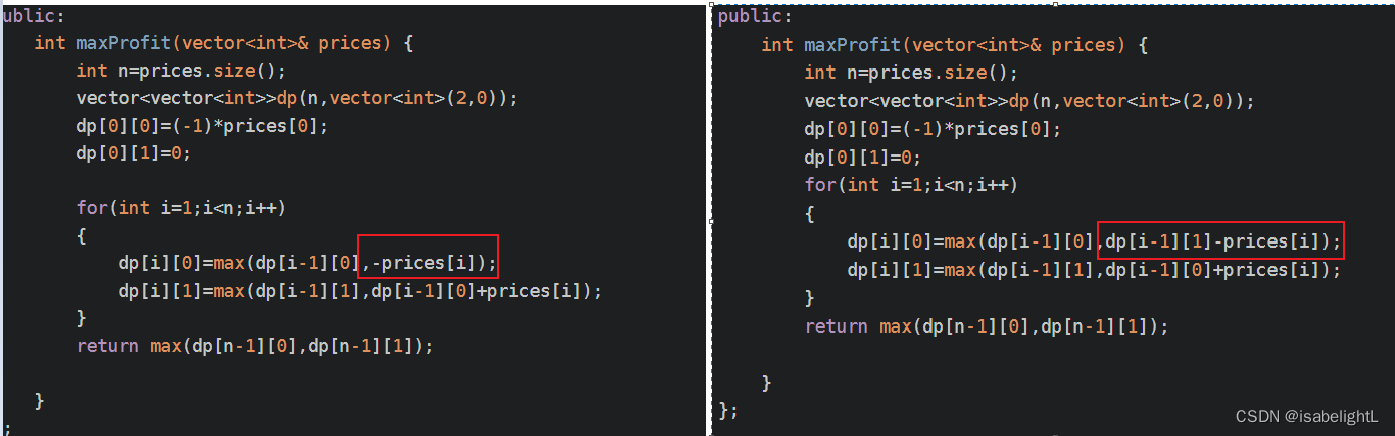
class Solution { /* 动态规划: 1、定义:dp[i][0]、dp[i][1]为持有股票的当前所有最大钱 买的行为:dp[i][0] 之前买过,保持买的状态 之前没买 卖的行为:dp[i][1] 之前已经卖啦,现在保持卖掉的状态 之前没有卖 2、 买的状态变化,第i天, 保持之前变化,dp[i][0]=dp[i-1][0] 今天我胡汉三就要买入股票!由于这道题的性质,肯定是第一次买入,dp[i][0]=-prices[i] 卖的状态变化,第i天 保持之前的状态,dp[i][1]=dp[i-1][1] 我胡汉三要在今天卖股票,dp[i][1]=dp[i-1][0]+prices[i] 3、初始值 第0天(在买的情况下)能持有的最大资产 dp[0][0]=-prices[i] 第0天(在卖的情况下)能持有的最大资产,//第一天不能既买又卖,最大值为0 dp[0][1]=0 */ public: int maxProfit(vector<int>& prices) { int n=prices.size(); vector<vector<int>>dp(n,vector<int>(2,0)); dp[0][0]=(-1)*prices[0]; dp[0][1]=0; for(int i=1;i<n;i++) { dp[i][0]=max(dp[i-1][0],-prices[i]); dp[i][1]=max(dp[i-1][1],dp[i-1][0]+prices[i]); } return max(dp[n-1][0],dp[n-1][1]); } };
122.买卖股票的最佳时机II
链接:代码随想录
这道题有贪心和动态规划两种解法,贪心前面已经写过,而且我二刷竟然记得!喜极而泣。
贪心解法:
class Solution { //二刷-----贪心解法,把差值为正的全部相加 public: int maxProfit(vector<int>& prices) { int n=prices.size(); int sum=0; for(int i=1;i<n;i++) { int temp=prices[i]-prices[i-1]; if(temp>0) { sum+=temp; } } return sum; } };动态规划:
直接看答案吧,自己做想不出啦。
视频链接:动态规划,股票问题第二弹 | LeetCode:122.买卖股票的最佳时机II_哔哩哔哩_bilibili
class Solution { /* 同买卖股票的最佳时机I相同的是: 任何时候 最多 只能持有 一股 股票 同买卖股票的最佳时机I不同的是:可以多次买入和卖出股票,只要自己手上同一时刻只有一股而不是多股就可以 所以要考虑买股票时,自己手上的资产可能并不为0.只有这一点不同 */ public: int maxProfit(vector<int>& prices) { int n=prices.size(); vector<vector<int>>dp(n,vector<int>(2,0)); dp[0][0]=(-1)*prices[0]; dp[0][1]=0; for(int i=1;i<n;i++) { dp[i][0]=max(dp[i-1][0],dp[i-1][1]-prices[i]); dp[i][1]=max(dp[i-1][1],dp[i-1][0]+prices[i]); } return max(dp[n-1][0],dp[n-1][1]); } };买卖股票I和买卖股票||的对比