前言

这是我讲的最后一个排序了，归并排序难度不大，也是分治的思想。

归并排序时间复杂度是在N*logN里面还是比较优的，毕竟实现起来的是完全二分的，但是差就差在了空间复杂度。

还是老样子，先给图解：

图解

大致思路

根据图也就看到了，是一个后序的处理，先分组再排序，跟快排不一样，快排是先排序再分组。

每一趟都是：先找最中间位置的下标mid，然后直接分成[left, mid] 和 [mid + 1, right]，然后等这两个有序了之后，再按顺序合并到一块。

但是排序前要开一个大小和原数据相同的数组。每一趟排完后，合并的时候得再这个新开的数组中合并，不然直接原数组合并的话是无法实现的。

代码实现

递归

这里写了一个子函数，因为不能每次都创建一个数组，要提前就开好。

//归并排序子函数
void _MergeSort(int* a, int left, int right, int* tmp)
{
	if (left >= right)
		return;

	int mid = (left + right) / 2;

	_MergeSort(a, left, mid, tmp);
	_MergeSort(a, mid + 1, right, tmp);

	//左区间
	int begin1 = left, end1 = mid;
	//右区间
	int begin2 = mid + 1, end2 = right;
	
	int i = begin1;

	//归并两个区间
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] > a[begin2])
			tmp[i++] = a[begin2++];
		else
			tmp[i++] = a[begin1++];
	}

	//右区间归并完了，左区间没归并完
	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1++];
	}

	//左区间归并完了，右区间没归并完
	while (begin2 <= end2)
	{
		tmp[i++] = a[begin2++];
	}

	//每次递归排序的位置是从left开始的，所以拷贝的时候要从这个位置拷贝
	memcpy(a + left, tmp + left, (right - left + 1) * sizeof(int));
}
 
 //归并排序
void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(n * sizeof(int));
	if (tmp == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}

	_MergeSort(a, 0, n - 1, tmp);
}

非递归

归并排序递归改非递归与斐波那契数列改为非递归的类似，要用到循环。

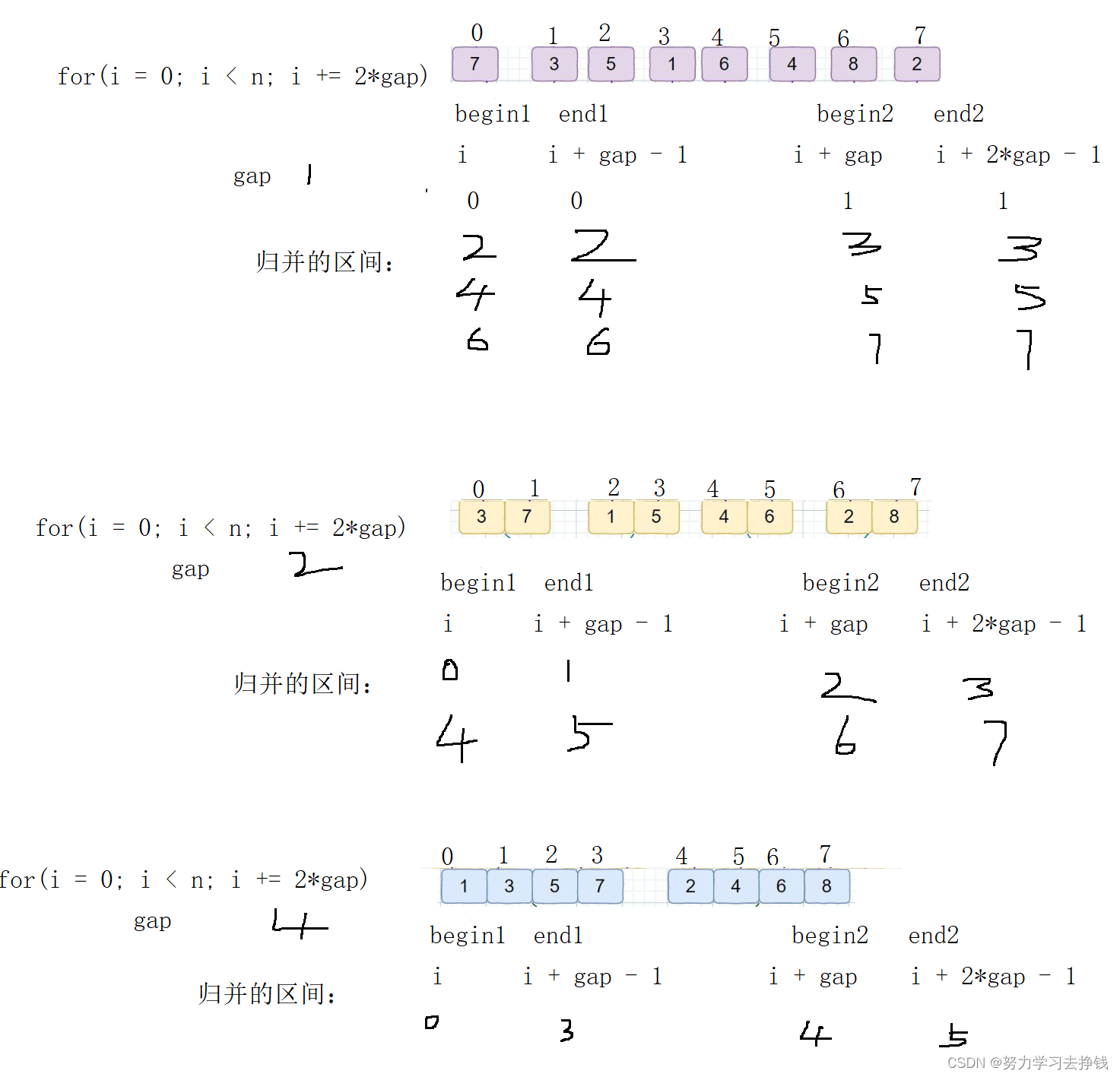
定义几个变量，当前趟的i，每次归并的时候两区间间隔位置gap
begin1 = i, end1 = i + gap - 1;
begin2 = i + gap, end2 = i + 2 * gap - 1;

每次归并的就是[begin1, end1] 和 [begin2, end2]两组的数。

大概图解：

代码实现

每次拷贝一大段：（推荐）

//归并非递归
void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(n * sizeof(int));
	if (tmp == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}

	//初始gap为1
	int gap = 1;

	while (gap < n)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;

			//调整越界区间
			if (end1 >= n)
			{
				end1 = n - 1;
				begin2 = n;
				end2 = n - 1;
			}
			else if (begin2 >= n)
			{
				begin2 = n;
				end2 = n - 1;
			}
			else if (end2 >= n)
			{
				end2 = n - 1;
			}

			int j = begin1;

			//归并两个区间
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] > a[begin2])
					tmp[j++] = a[begin2++];
				else
					tmp[j++] = a[begin1++];
			}

			//右区间归并完了，左区间没归并完
			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}

			//左区间归并完了，右区间没归并完
			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}

		}
		memcpy(a, tmp, n * sizeof(int));
		gap *= 2;
	}
}

第二种：每次拷贝一小段

//归并非递归
void MergeSortNonR2(int* a, int n)
{
	int* tmp = (int*)malloc(n * sizeof(int));
	if (tmp == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}

	//初始gap为1
	int gap = 1;

	while (gap < n)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;

			//调整越界区间
			if (end1 >= n || begin2 >= n)
			{
				break;
			}
			else if (end2 >= n)
			{
				end2 = n - 1;
			}

			int sn = end2 - begin1 + 1;
			int begin = begin1;
			int j = begin1;

			//归并两个区间
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] > a[begin2])
					tmp[j++] = a[begin2++];
				else
					tmp[j++] = a[begin1++];
			}

			//右区间归并完了，左区间没归并完
			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}

			//左区间归并完了，右区间没归并完
			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}
			memcpy(a + begin, tmp + begin, sn * sizeof(int));
		}
		gap *= 2;
	}
}

时间复杂度和空间复杂度

时间O(N * logN)
空间O(N)，每次排序前都要开辟相同大小的数组。

到此结束。