在机器学习算法中,马尔可夫链(Markov chain)是个很重要的概念。马尔可夫链(Markov chain),又称离散时间马尔可夫链(discrete-time Markov chain),因俄国数学家安德烈·马尔可夫(俄语:Андрей Андреевич Марков)得名。
马尔科夫链即为状态空间中从一个状态到另一个状态转换的随机过程。
该过程要求具备“无记忆”的性质:
下一状态的概率分布只能由当前状态决定,在时间序列中它前面的事件均与之无关。这种特定类型的“无记忆性”称作马尔可夫性质。
马尔科夫链作为实际过程的统计模型具有许多应用。
在马尔可夫链的每一步,系统根据概率分布,可以从一个状态变到另一个状态,也可以保持当前状态。
状态的改变叫做转移,与不同的状态改变相关的概率叫做转移概率。
马尔可夫链的数学表示为:
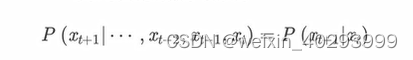
既然某一时刻状态转移的概率只依赖前一个状态,那么只要求出系统中任意两个状态之间的转移概率,这个马尔科夫链的模型就定了。
马尔科夫链即为
状态空间中从一个状态到另一个状态转换的随机过程。
该过程要求具备“无记忆”的性质:
下一状态的概率分布只能由当前状态决定,在时间序列中它前面的事件均与之无关。
隐马尔可夫模型(Hidden Markov Model,HMM)是统计模型,它用来描述一个含有隐含未知参数的马尔可夫过程。
其难点是从可观察的参数中确定该过程的隐含参数。然后利用这些参数来作进一步的分析,例如模式识别。