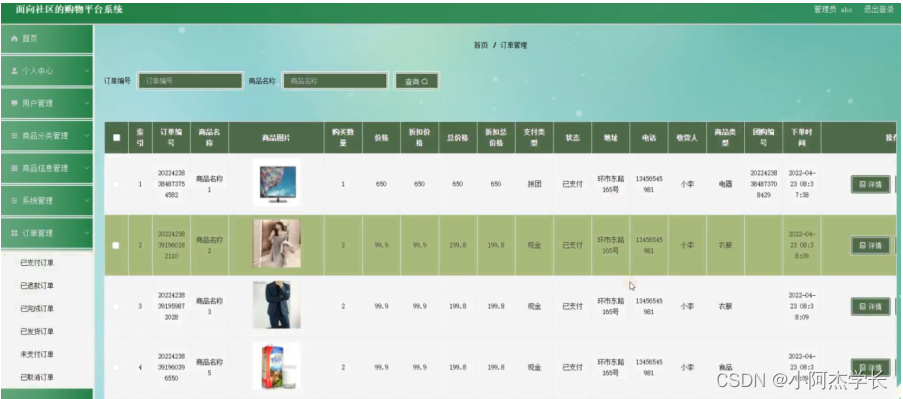
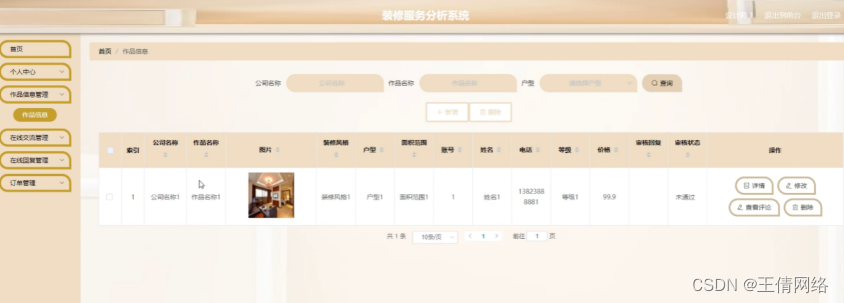
题目描述

简单来说就给一个N*N的棋盘 棋盘上的每一列每一行以及每一个对角不能出现两个皇后
因此明确以下几点

• 要找出所有可能的解法
• 也是采用回溯法进行求解（具体在下面进行详解）

用下面一张示例图来说明回溯法的思路

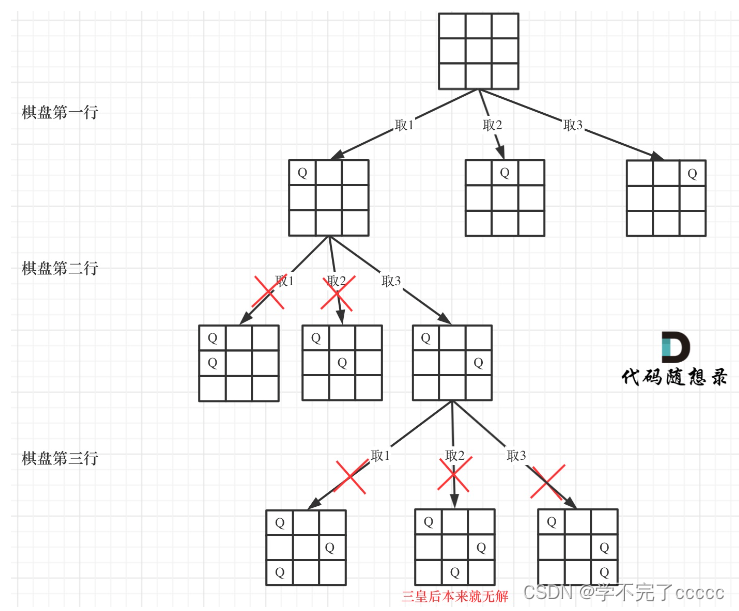
说白了就是进行搜索， 每行进行搜索 行内再进行列搜索（每行的搜索用递归控制，行内每列的搜索用for循环进行控制） 那么当前位置符合我们的要求（行列对角线无其他皇后）将皇后放入
剩下的就是回溯法的正常流程了
那么递归函数的参数是什么呢，首先必须有在哪一行即行号，棋盘大小n也必须有，还有最重要的就是我们的棋盘（在主函数里人为构造）
还有一点就是判断当前位置放入皇后是否合法的问题（在代码注释里）

• 列
• 两个对角（45°和135°）

代码实现

class Solution {
private:
    vector<vector<string>> result;
    // row 代表行号
    void backtracking(int row, int n, vector<string>& chess_board)
    {	// 访问到最后一行即结束
        if(row == n)
        {
            result.push_back(chess_board);
            return;
        }
        for(int i=0; i<n; i++)
        {	// 行内列的遍历搜索 当前位置符合要求即插入
            if(isValid(i, row, chess_board, n))
            {
                chess_board[row][i] = 'Q';
                backtracking(row+1, n, chess_board);
                chess_board[row][i] = '.';  // 回溯
            }
        }
    }
    // 判断当前位置是否有效  col列号  row行号
    bool isValid(int col, int row, vector<string>& chess_board, int n)
    {
        // 列
        for(int i = 0; i<row; i++)
        {	// 列号确定   遍历该列的每一行 
            if(chess_board[i][col]=='Q')
            {
                return false;
            }
        }
        // 45°
        for(int i = row-1, j=col+1; i>=0 && j<n; i--, j++)
        {	// 45 °的对角线位置  重点是 i>=0 && j<n 这个条件并起来狠关键
            if(chess_board[i][j]=='Q')
            {
                return false;
            }
        }
        // 135
        for(int i = row-1, j = col-1; i>=0 && j>=0; i--, j--)
        {	
            if(chess_board[i][j]=='Q')
            {
                return false;
            }
        }
        return true;
    } 
public:
    vector<vector<string>> solveNQueens(int n) {
    	// 创建一个n*n的棋盘用.来填充
        std::vector<std::string> chess_board(n, std::string(n, '.'));
        backtracking(0, n, chess_board);
        return result;
    }
};