目录
一、前言
二、线性规划简介
1、线性规划模型介绍与特征
2、线性规划模型的一般形式
三、单纯形法
1、标准化
2、单纯形法解题
四、matlab解决问题1、matlab线性规划函数
2、解题代码
一、前言
数学建模,本意就是用来解决生活中的问题,我们今天想讲一讲装修的相关问题。没错,我们的伍老师通过自己赚的钱,斥巨资买了一套单身公寓。买完单身公寓后,伍老师发现,装修有杂七杂八的一系列问题,太麻烦了!此时伍老师的男朋友小李站出来了,对伍老师特别man的说:“别担心,这不是还有我吗,我来处理这些事情好了!”但是小李是一个四肢发达,头脑简单的人,对装修更是一窍不通。但是牛皮已经吹出去了,话再收回来就要被啪啪打脸了。所以,为了维护小李作为男人的尊严,我们今天就需要帮一下小李。
引例:伍老师刚拿到毛坯房,觉得房子里面空气质量太差了,于是决定买一些花朵来改善一下房子里的空气。已知伍老师看中了满天星、向日葵、洋桔梗以及红玫瑰四个品种。其单价、功效与装饰效果如下:
A.洋桔梗:每平方米75元,一天能净化0.8千克空气,装饰效果评分为2颗星
B.满天星:每平方米130元,一天能净化0.72千克空气,装饰效果评分为7颗星
C.向日葵:每平方米105元,一天能净化0.75千克空气,装饰效果评分为6颗星
D.红玫瑰:每平方米200元,一天能净化0.65千克空气,装饰效果评分为10颗星
已知,伍老师打算拿出一千块买花,预计拿出20平方米的空间放绿植,且希望装饰效果评分不低于45颗星,那么如何购买能使空气质量净化效果最佳?

二、线性规划简介
1、线性规划模型介绍与特征
线性规划(Linear Programming,缩写为LP)通常研究资源的最优利用、设备最佳运行等问题。例如,当任务或目标确定后,如何统筹兼顾,合理安排,用最少的资源(如资金、设备、原标材料、人工、时间等)去完成确定的任务或目标;企业在一定的资源条件限制下,如何组织安排生 产获得最好的经济效益(如产品量最多 、利润最大)。
线性规划的数学模型由决策变量 Decision variables 、目标函数Objective function 与约束条件Constraints 构成。称为线性规划三要素。
线性规划模型的特征是:
1.解决问题的目标函数是多个决策变量的线性函数,通常是求最大值或最小值;
2.解决问题的约束条件是一组多个决策变量的线性不等式或等式。
2、线性规划模型的一般形式
一般地,假设线性规划数学模型中,有m个约束,有n个决策变量xj, j=1,2…,n,目标函数的变量系数用cj表示, cj称为价值系数。约束条件的变量系数用aij表示,aij称为工艺系数。约束条件右端的 常数用bi表示,bi称为资源限量。则线性规划数学模型的一般表达式可写成:
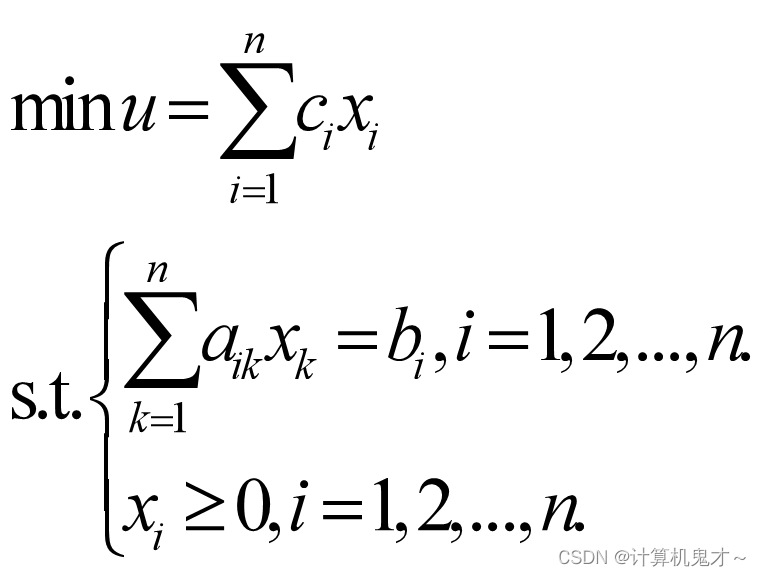
由此,引例的线性规划模型可以写为:
设xj(j=1,2,…,4)分别代表洋桔梗、满天星、向日葵以及红玫瑰所占面积(平方米),得到下列线性规划模型:
三、单纯形法
如何解出线性规划问题的解?很简单,学过高中数学的同学们应该知道:画图嘛,画二维平面图可以解决两个变量的线性规划问题,画空间涂可以解决三个变量的线性规划问题。那么四个变量、五个变量的呢?大家是想让自己变为高纬度生物,再解出题目呢,还是用其他方法解出来?诶嘿,还真有一种方法解决线性规划问题,叫做单纯形法,请听小编娓娓道来。
1、标准化
在用单纯法求解线性规划问题时,为了讨论问题方便,需将线性规划模型化为统一的标准形式。 线性规划问题的标准型为:
1.目标函数求最大值
2.约束条件都为等式方程
3.变量xj非负
4.常数bi非负
5.在≤左端加入松驰变量 (slack variable);在≥号左端减去剩余变量(Surplus variable)
6.目标函数是最小值,为了化为求最大值,令Z′ =-Z,得到 max Z′ =-Z
那么,例题的标准化模型为:
2、单纯形法解题
计算步骤:
1.求初始基可行解,列出初始单纯形表,求出检验数。其中
基变量的检验数必为零;
2.判断:
(a)若λj≤0(j=1,2,…,n)得到最优解;
(b)某个λk>0且aik≤0(i=1,2,…,m)则线性规划具有无界解(见例1-18)。
(c)若存在λk>0且aik (i=1,…,m)不全非正,则进行换基;
3.换基:
(a)选进基变量 :设λk=max{λj | λj >0},xk为进基变量
(b)选出基变量 ,求最小比值:
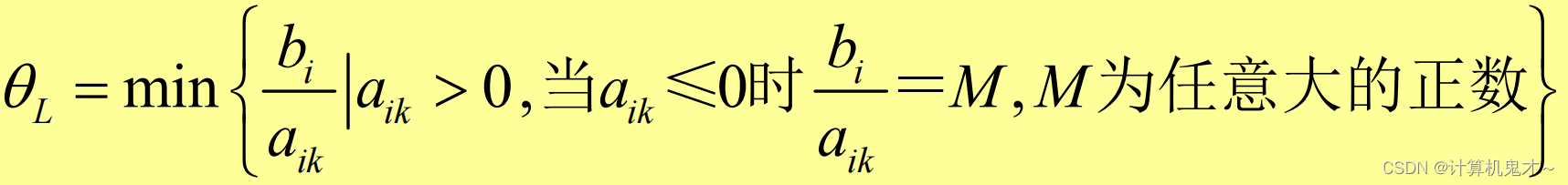
第L个比值最小 ,选最小比值对应行的基变量为出基变量, 若有相同最小比值,则任选一个。aLk为主元素。
(c)求新的基可行解:用初等行变换方法将aLk 化为1,k列其它元素化为零(包括检验数行)得到新的可行基及基本可行解,再判断是否得到最优解。
四、matlab解决问题
1、matlab线性规划函数
其实单纯形法在数学建模里面只作为了解即可,因为我们更偏重于动手编程能力。在MATLAB里面,有一个专门解决线性规划的函数,叫做linprog,其函数与参数含义如下:
①x=linprog(c, A, b)
注意:A与b均为矩阵的形式
②x=linprog(c,A,b,Aeq,beq)
注意:1.若没有不等式: 存在,则令A=[ ],b=[ ]
2.A、Aeq、b、beq均为矩阵的形式
③x=linprog(c,A,b,Aeq,beq, VLB,VUB)
注意:1.若没有等式约束: , 则令Aeq=[ ], beq=[ ]
2. A、Aeq、b、beq、VLB、VUB均为矩阵的形式
2、解题代码
c=[-0.8 -0.72 -0.75 -0.65];
A=[-2 -7 -6 -10;75 130 105 200];
b=[-45 ; 1000];
Aeq=[];
beq=[];
vlb=[0,0,0,0];
vub=[];
[x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub);
-fval,x结果为:
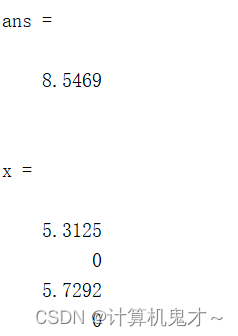
由此可见,洋桔梗买5.3125平方米,向日葵买5.7292平方米时,既能保证在预算之内,又能让房子更加温馨有氛围,同时也能净化最多的空气!看得出来,伍老师还有小李与向日葵以及洋桔梗是绝配,更可能是因为,伍老师就是小李的太阳,给予小李足够多的温暖,就和向日葵一样!
好的,本期的算法课就到这里结束啦,感兴趣的小伙伴们给小编点一个小心心可好?