数字水印概念

数字水印是一种将特定数字信息嵌入到数字作品中从而实现信息隐藏、版权认证、完整性认证、数字签名等功能的技术。

以图片水印为例:

水印嵌入过程:版权信息水印A嵌入到图像B中,得到含有水印的图像C,图像C与图像B在外观上基本一致，肉眼无法区分差异。

水印提取过程:通过水印提取技术，将图像C中的水印提取得到删除水印的D和提取的水印E，图像C应和图像D在外观上基本一致，同时肉眼无法区分，另外，水印E应和水印A一致。

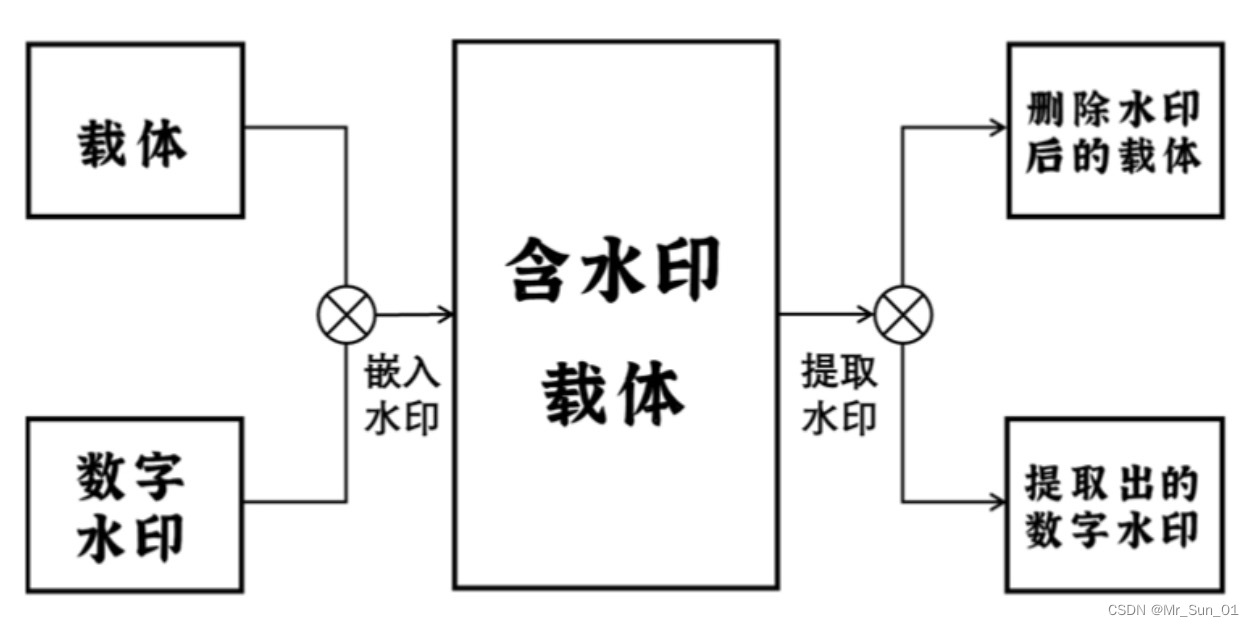
同样的，为了保证嵌入水印前后肉眼不能够观察到差异，必须确保嵌入的水印对载体的影响较小，这就要求嵌入的位置隐藏在相对不重要的位置。

而我们知道的，在一个多位的10进制数字中，修改高位的数值比修改低位的数值对数值的影响要大的多，同样的，修改载体图像像素点的最低位来实现水印的嵌入，对载体图像的影响也是最小的。这就延伸出一个新的概念--位平面。

位平面

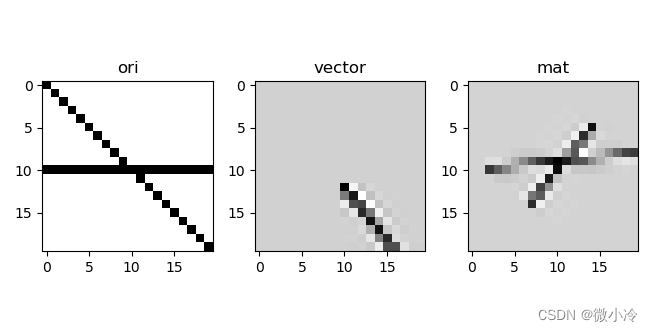
提取灰度图像中所有像素点的二进制形式像素值中处于同一比特位上的值，得到一副二值图像，该图像被称为灰度图像的一个位平面，其他位平面的过程成为位平面分解。

任意 x ∈[0,255]都满足x =a8 * 2^7 + a7 * 2^6 + a6 * 2^5 + a5 * 2^4 + a4 * 2^3 + a3 * 2^2 + a2 * 2^1 + a1 * 2^0 ，其中 a1、a2、a3、a4、a5、a6、a7、a8等于0或者1。

点位图分解就是对所有像素点的值分别取出所有的a1、a2、a3、a4、a5、a6、a7、a8到一个独立的数组中，这些数组就是位平面，取出的位平面是个二值图。涉及比特位取位运算，关键操作当然少不了与运算。

另外，显示位平面时，低位取出的位平面趋近为黑色。具体操作为位平面RD的像素点大于0(有值)时置为true，等于0的位置置为false形成一个模板mask，再对模板位置为true的位置置为255，具体如下:

mask = ( RD > 0 )

RD[ mask ] = 255

简化后为:RD[ RD > 0 ] = 255

获取图像的位平面代码如下:

import cv2 as cv
import numpy as np

# 读取原始图
lena = cv.imread("lena.png", 0)
cv.imshow("lena", lena)

r, c = lena.shape
# 获取位平面当然是用比特位与运算
# 8个位平面对应需要8个与图像等宽高的矩阵
x = np.zeros((r, c, 8), dtype=np.uint8)
for i in range(8):
    x[:, :, i] = 2 ** i  # 每个矩阵填充做与运算的数值
    # cv.imshow(str(i),x[:,:,i])#为什么后面要做阈值处理,这里可以看出,只有6,7稍微白一些,0-5都挺黑的

# 用来保存位平面结果的数组
result_images = np.zeros((r, c, 8), dtype=np.uint8)
for i in range(8):
    # 原图和矩阵进行与运算,并把结果保存好
    result_images[:, :, i] = cv.bitwise_and(lena, x[:, :, i])  # 与运算后得到一个灰度图(里面只有0和位值)

    mask = result_images[:, :, i] > 0  # 灰度图中值大于0的位置为true,等于0的位置为false,得到一个掩模
    result_images[mask] = 255  # 根据掩模进行处理,灰度图变成了二值图
    cv.imshow(str(i), result_images[:, :, i])

cv.waitKey()
cv.destroyAllWindows()

程序运行如下: