【数据统计】— 极大似然估计 MLE、最大后验估计 MAP、贝叶斯估计
- 极大似然估计、最大后验概率估计(MAP),贝叶斯估计
- 极大似然估计(Maximum Likelihood Estimate,MLE)
- MLE目标
- 例子: 扔硬币
- 极大似然估计—高斯分布的参数
- 矩估计 vs LSE vs MLE
- 贝叶斯公式:
极大似然估计、最大后验概率估计(MAP),贝叶斯估计
极大似然估计(Maximum Likelihood Estimate,MLE)
- 思想:利用已知的样本结果信息,反推最具有可能(最大概率)导致这些样本结果出现的模型参数值
- 模型已定,参数未知
- 目标:概率分布函数或者似然函数最大
- 用似然函数取到最大值时的参数值作为估计值
- 概率分布模型
- 伯努利分布
- 二项分布
- 高斯分布
- 泊松分布

MLE目标
- 目标:用似然函数取到最大值时的参数值作为估计值
- 设总体分布为𝑓 𝑋 𝜃 ,𝑥1, 𝑥2, 𝑥3, ⋯,𝑥𝑁为样本。样本满足独立同分布,则他们的联合密度函数为:

- 其中,𝜃为未知参数。样本已经存在(观测),即,𝑥1, 𝑥2, 𝑥3, ⋯,𝑥𝑛是固定的。 L(𝑋|𝜃)是关于𝜃的函数,称为似然函数
- 目标:求参数𝜃,使似然函数取极大值,称为极大似然估计
- 实践中,通常对似然函数取对数(log或ln)(连乘运算变为连加运算),即对数似然函数。所以,极大似然估计问题可以写成

例子: 扔硬币
- X每次实验𝑋𝑖服从伯努利分布
- 参数为𝜽,假设为事件(正面向上)发生的概率

- 参数为𝜽,假设为事件(正面向上)发生的概率
- n次实验,共k次正面向上,采用MLE估计参数𝜽:


极大似然估计—高斯分布的参数
- 例:给定𝑥1, 𝑥2, 𝑥3, ⋯,𝑥𝑁为样本,已知样本来自于高斯分布 𝑁 𝜇, 𝜎 ,估计参数𝜇,𝜎

矩估计 vs LSE vs MLE
贝叶斯公式:

- 它将后验概率转化为基于似然函数和先验概率的计算表达式:
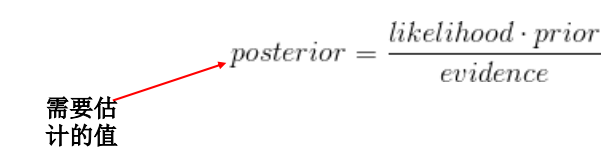

![[golang gin框架] 25.Gin 商城项目-配置清除缓存以及前台列表页面数据渲染公共数据](https://img-blog.csdnimg.cn/img_convert/4cf1d963a7e04e8ea7427a3ab94f1708.png)