目录

二叉搜索树的插入

思路图解

代码实现

要点 

例题

二叉搜索树的删除

情况一

情况二

情况三 

右子树的最小元素

左子树的最大元素 

代码实现

---

二叉搜索树的插入

要进行二叉搜索树的插入，

关键点在于要找到元素应该插入到哪个位置，可以采用与Find类似的方法，

将要插入的节点与根节点进行比较，如果大于根节点，就往右边走；

若小于根节点，就往左边走；

直到某一个节点的左子树或者右子树为空就停止，进行节点的插入操作。

思路图解

代码实现

BinTree Insert(ElementType x, BinTree BST)
{
	if (!BST)    //若树为空，则创建并返回一个节点的二叉搜索树
	{
		BST = malloc(sizeof(struct TreeNode));
		BST->data = x;
		BST->Left = BST->Right = NULL;
	}
	else if (x > BST->data)     //开始查找要插入元素的位置
	{
		BST->Right = Insert(x, BST->Right);   //递归进入右子树
	}
	else if (x < BST->data)
	{
		BST->Left = Insert(x, BST->Left);    //递归进入左子树
	}
	//else
	//{
	//	//x匹配成功，则说明都不做
	//}
	return BST;
}

要点 

需要注意的是：

当找到了新节点应该插入的位置时，需要通过找到上一个节点的地址，来将上一个节点的左子树指针或者右子树指针指向新节点。

例如：

例题

以一年十二个月的英文缩写为键值，按从一月到十二月的顺序输入

即输入序列为：

Jan、Feb、Mar、Apr、May、Jun、July、Aug、Sept、Oct、Nov、Dec。

它形成的二叉搜索树是怎样的呢？ 

这里月份缩写键值的比较，按照的是字母在字典中的排序大小，如A最小，Z最大。如果第一个字母相同，则继续比较第二个字母。

形成的二叉搜索树就为：

 

二叉搜索树的删除

二叉搜索树的删除需要考虑三种情况：

情况一

1.要删除的节点是叶节点：

那么就可以直接删除，并再修改该节点的父节点指针——置为空。

例：

情况二

2.要删除的节点只有一个孩子节点：

那么就将该节点的父节点的指针指向要删除节点的孩子节点。

例：

情况三 

3.要删除的节点有左、右两颗子树：

这种情况是比较复杂的，我们把复杂的问题问题转换为简单的问题。

我们已经知道了没有孩子节点的情况和只有一个孩子节点的情况该怎么删除了，当有两个孩子节点的情况时，就考虑能不能把它变成只有一个孩子节点的情况来处理呢？

是可以实现的：用另一节点替代被删除的节点，这个节点应是右子树的最小元素或者左子树的最大元素。

例：

右子树的最小元素

左子树的最大元素 

 

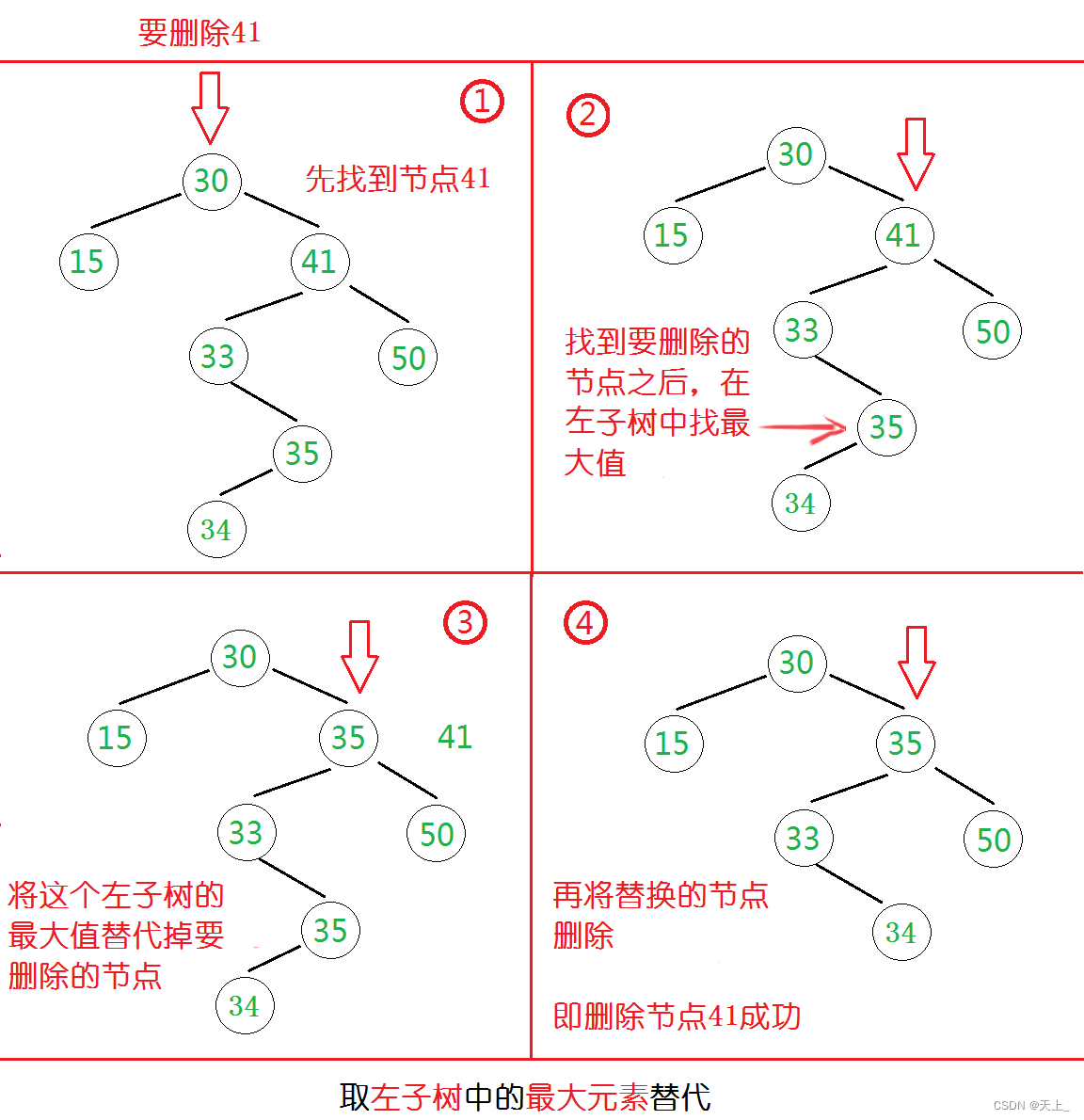
 所以删除节点有两个孩子节点的情况下，我们就变成了在右子树找最小元素或者在左子树找最大元素的问题了。这样处理的好处是：左子树的最大值一定不是有两个孩子节点的情况、而右子树的最小值也一定不是有两个孩子节点的情况。

代码实现

BinTree Delete(ElementType x, BinTree BST)
{
	Position Tmp;
	if (!BST)
	{
		printf("要删除的元素未找到\n");
	}
	else if (x < BST->data)
	{
		BST->Left = Delete(x, BST->Left);  //查找节点，往左子树递归
	}
	else if (x > BST->data)
	{
		BST->Right = Delete(x, BST->Right);//查找节点，往右子树递归
	}
	else                                   //找到了要删除的节点
	{
		if (BST->Left && BST->Right)     //被删除的节点有左右两个孩子节点
		{
			Tmp = FindMin(BST->Right);   //在右子树中找到最小元素
			BST->data = Tmp->data;       //将最小元素填充到要删除的节点位置
			BST->Right = Delete(BST->data, BST->Right);
			//在要删除节点的右子树里删除那个最小元素
		}
		else                             //被删除的节点只有一个孩子节点或者没有孩子节点
		{
			Tmp = BST;
			if (!BST->Left)              //有右孩子节点或者没有孩子节点
			{
				BST = BST->Right;
			}
			else if (!BST->Right)        //有左孩子节点或者没有孩子节点
			{
				BST = BST->Left;
			}
			free(Tmp);
		}
	}
	return BST;
}

 

---

end

---

学习自：MOOC数据结构——陈越、何钦铭