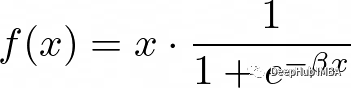作者：宫崎修一 石田保辉

◆ 1-3 数组

在链表和数组中，数据都是线性地排成一列。在链表中访问数据较为复杂，添加和删除数据较为简单；而在数组中访问数据比较简单，添加和删除数据却比较复杂。

◆ 1-6 哈希表

在存储数据的过程中，如果发生冲突，可以利用链表在已有数据的后面插入新数据来解决冲突。这种方法被称为“链地址法”。除了链地址法以外，还有几种解决冲突的方法。其中，应用较为广泛的是“开放地址法”。这种方法是指当冲突发生时，立刻计算出一个候补地址（数组上的位置）并将数据存进去。如果仍然有冲突，便继续计算下一个候补地址，直到有空地址为止。可以通过多次使用哈希函数或“线性探测法”等方法计算候补地址。

◆ 1-8 二叉查找树

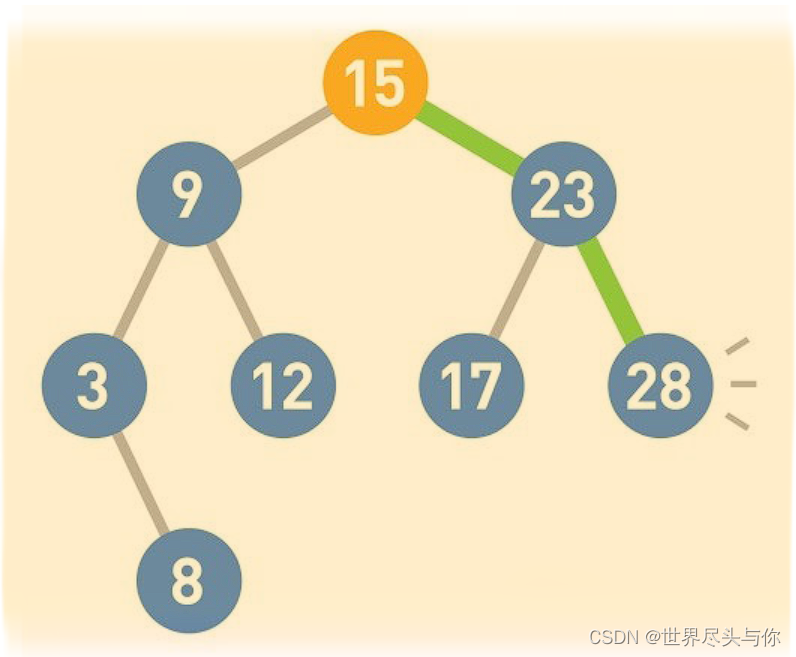
二叉查找树有两个性质。第一个是每个结点的值均大于其左子树上任意一个结点的值。

第二个是每个结点的值均小于其右子树上任意一个结点的值。

根据这两个性质可以得到以下结论。首先，二叉查找树的最小结点要从顶端开始，往其左下的末端寻找。此处最小值为3。

反过来，二叉查找树的最大结点要从顶端开始，往其右下的末端寻找。此处最大值为28。

◆ 2-7 快速排序

快速排序是一种“分治法”。它将原本的问题分成两个子问题（比基准值小的数和比基准值大的数），然后再分别解决这两个问题。子问题，也就是子序列完成排序后，再像一开始说明的那样，把他们合并成一个序列，那么对原始序列的排序也就完成了。

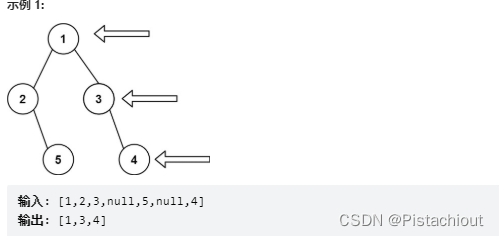
◆ 4-2 广度优先搜索

广度优先搜索的特征为从起点开始，由近及远进行广泛的搜索。因此，目标顶点离起点越近，搜索结束得就越快。

◆ 4-3 深度优先搜索

深度优先搜索的特征为沿着一条路径不断往下，进行深度搜索。虽然广度优先搜索和深度优先搜索在搜索顺序上有很大的差异，但是在操作步骤上却只有一点不同，那就是选择哪一个候补顶点作为下一个顶点的基准不同。广度优先搜索选择的是最早成为候补的顶点，因为顶点离起点越近就越早成为候补，所以会从离起点近的地方开始按顺序搜索；而深度优先搜索选择的则是最新成为候补的顶点，所以会一路往下，沿着新发现的路径不断深入搜索。

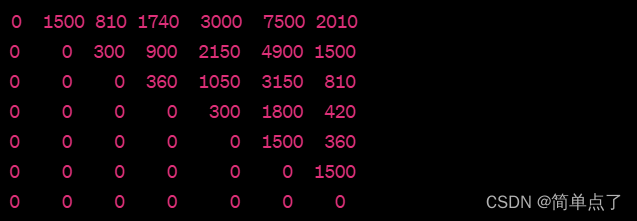
◆ 4-5 狄克斯特拉算法

比起需要对所有的边都重复计算权重和更新权重的贝尔曼-福特算法，狄克斯特拉算法多了一步选择顶点的操作，这使得它在求最短路径上更为高效。

总的来说，就是不存在负数权重时，更适合使用效率较高的狄克斯特拉算法，而存在负数权重时，即便较为耗时，也应该使用可以得到正确答案的贝尔曼-福特算法。

◆ 4-6 A*算法

如果我们能得到一些启发信息，即各个顶点到终点的大致距离（这个距离不需是准确的值）我们就能使用A算法。当然，有时这类信息是完全无法估算的，这时就不能使用A算法。

距离估算值越接近当前顶点到终点的实际值，A*算法的搜索效率也就越高；反过来，如果距离估算值与实际值相差较大，那么该算法的效率可能会比狄克斯特拉算法的还要低。如果差距再大一些，甚至可能无法得到正确答案。

◆ 5-3 哈希函数

输入相似的数据并不会导致输出的哈希值也相似。

◆ 6-2 k-means算法

k-means算法中，随着操作的不断重复，中心点的位置必定会在某处收敛

由于k-means算法需要事先确定好簇的数量，所以设定的数量如果不合理，运行的结果就可能会不符合我们的需求。

在层次聚类算法中，一开始每个数据都自成一类。也就是说，有n个数据就会形成n个簇。然后重复执行“将距离最近的两个簇合并为一个”的操作n-1次。每执行1次，簇就会减少1个。执行n-1次后，所有数据就都被分到了一个簇中。在这个过程中，每个阶段的簇的数量都不同，对应的聚类结果也不同。只要选择其中最为合理的1个结果就好。

◆ 7-2 素性测试

实际上不只是5，对于任意素数p，下面的公式都是成立的。这就是“费马小定理”。根据是否满足费马小定理来判断一个数是否为素数的方法就是“费马测试”。