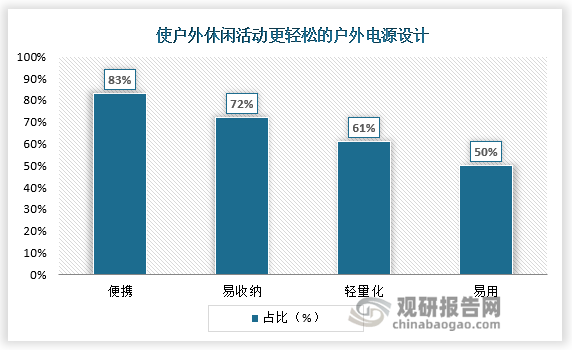
在WSN定位中常常采用三边定位算法,试画图推导三边定位的计算公式,并表示为矩阵形式。

目录
1. 实验目标
2. 实验要求
3. 算法介绍
3.1基本内容介绍
3.2迭代多边定位算法
3.3 DV-HOP算法
4. 算法实现
4.1迭代多边定位算法
第一步:将数据读入内存
第二步:判断锚节的个数
第三步:初始化距离矩阵
第四步:迭代计算
核心代码
(1)计算未知节点位置
(2)更新锚节点、非锚节点集合以及距离矩阵
第五步:计算误差,输出结果
4.2 DV-HOP算法
第一步:将数据读入内存
第二步:判断锚节的个数
第三步:将所有的两点间的距离关系读入距离矩阵
第四步:利用最短路径算法求得两点间的最短路径
第五步:求每个信标节点的校正值
第六步:未知节点计算位置
第七步:计算误差,输出结果
5.实验结果和分析
5.1 迭代多边定位算法
1、实验结果
2、误差分析
5.2DV-HOP算法
1、实验结果
2、误差分析
物联网定位技术
实验报告
| 学生姓名 | 白** |
| 学 号 | 2008070101 |
| 专业班级 | 物联201 |
| 指导老师 | 曾** |
| 学 院 | 信息学院 |
| 完成时间 | 2023年3月23日 |
实验2 多边定位算法、DV-HOP算法
1. 实验目标
了解典型的无线传感器网络定位算法;
在所给的网络中实现所讲授的无线传感器网络定位算法并进行比较。
2. 实验要求
掌握典型的无线传感器网络定位算法基本原理,理解多边定位算法、DV-HOP算法。
利用所给的网络数据,实现两种以上的定位算法并进行比较。
3. 算法介绍
3.1基本内容介绍
在本次实验中,共有四个已知的.txt文件,分别命名为:net1_pos.txt、net1_topo_error_free.txt、net1_topo_error_5以及net1_topo_error_10。
其中,文件net1_pos中给出了实验网络中节点的位置数据。每行表示一个节点的位置信息。格式如下:
节点序号 节点x坐标 节点y坐标 是否锚节点(1代表锚节点,0代表待定位节点),比如:
1 17.8977 106.2282 1
表示节点1, 其真实位置为(17.8977,106,2282),该节点是锚节点。再比如:
33 43.4718 95.7603 0
表示节点33,其真实位置是(43.4718,95.7603),该节点是待定位节点。利用某种定位算法计算出来待定位节点的位置后,就可以根据真实位置计算该节点的定位误差。
文件 net1_topo_error_free中给出了网络中相邻节点之间的距离信息。每一行表示两个节点之间的距离。格式如下:
节点1序号 节点2序号 节点之间距离测量值。比如:
1 4 8.3075
表示节点1和节点4可以相互测量出之间的距离,他们之间的距离是8.3075;
文件net1_topo_error_5和net1_topo_error_10给出的距离分别是增加了5%和10%误差之后的扰动值。
3.2迭代多边定位算法
算法思想:利用已知信标节点和非信标节点的几组对应关系(两点间距离),对非信标节点进行定位。(某个非信标节点只要已知3个及以上信标节点与其距离即可对其进行定位。)定位成功后的非信标节点转换为信标节点,可辅助对其他非信标节点定位。不断迭代定位过程,知道信标节点集合元素个数在前后两次迭代中数量不变,则迭代终止。
前提条件:已知位置的锚节点个数要超过3个;对所有节点来说,在添加完邻接矩阵关系后,是一个连通图,没有孤立节点。
特别说明:因为在使用迭代多边定位算法对未知节点进行定位时需要利用该节点与3个以上信标节点的直线距离,图是连通图但不是全连通图,所以可能会有部分节点无法定位。
3.3 DV-HOP算法
算法思想:先用Floyd算法将图的最短路径和每两个节点间的最小跳数表示出来,将特定位置的节点到参考节点的距离用网络中的节点的平均每跳距离和节点之间的跳数乘积表示,使用三角形定位的方法来获得节点的位置节点。
前提条件:已知位置的锚节点个数要超过3个;对所有节点来说,在添加完邻接矩阵关系后,是一个连通图,没有孤立节点。
特别说明:图是否为连通图对于迭代多边算法影响可能不会很大,但是在DV-HOP算法中,如果有孤立节点,则会导致程序出错。
4. 算法实现
4.1迭代多边定位算法
第一步:将数据读入内存
利用Matlab中已有的函数load将文件中的内容以矩阵的方式读入内存。
Data_post = load('net1_pos.txt');
Data_road1 = load('net1_topo-error free.txt');
Data_road2 = load('net1_topo-error 5.txt');
Data_road3 = load('net1_topo-error 10.txt');
culunm_post = size(Data_post);
第二步:判断锚节的个数
tempcount = 0;
for i = 1:culunm_post(1)
if Data_post(i,4) == 1
tempcount = tempcount+1;
end
end
if tempcount < 3
disp('锚节点少于3个,DV-hop算法无法执行');
return;
end
第三步:初始化距离矩阵
将与锚节点有关的路径读入距离矩阵,先将距离矩阵全部赋值为无穷大,再将每个节点到自身的距离规定为0,在边的信息中,如果有端点为锚节点的,就更新其两点间的距离。
for i = 1:culunm_road(1)
if(Data_road(i,1) <= anchors_n)
matrix(Data_road(i,1),Data_road(i,2)) = Data_road(i,3);
elseif(Data_road(i,2) <= anchors_n)
matrix(Data_road(i,2),Data_road(i,1)) = Data_road(i,3);
end
end
第四步:迭代计算
逐一判断每一个非信标节点是否有3个以上锚节点与其相关,如果有3个以上的信标节点与其相关则根据:
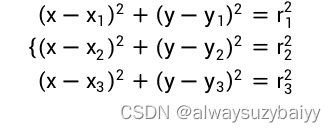
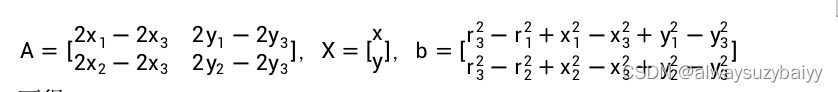
其中x,y为未定位的节点的实际位置(x1,y1),(x2,y2),……是已知的锚节点到该未知节点的距离。
根据以上两个矩阵的转换,可以求得:![]() ,其中x为一个一行两列的矩阵,分别表示未知节点定位后的坐标位置x,y。
,其中x为一个一行两列的矩阵,分别表示未知节点定位后的坐标位置x,y。
定位成功后,把该点的标号加入锚节点集合中并从非锚节点集合中删除,并在距离矩阵中加入与该节点相关的边的信息。
不断迭代运行第四步,直至锚节点集合中元素个数不再变化。
核心代码
(1)计算未知节点位置
point = temp(1,3)^2 - temp(1,1)^2 - temp(1,2)^2;
for ii = 2:k-1
A(ii-1,:) = 2*[temp(1,1) - temp(ii,1) temp(1,2) - temp(ii,2)];
b(ii-1,:) = [temp(ii,3)^2 - temp(ii,1)^2 - temp(ii,2)^2 - point];
end
Ans = inv(transpose(A)*A)*transpose(A)*b;
estimated(j,1) = Ans(1,1);
estimated(j,2) = Ans(2,1);
(2)更新锚节点、非锚节点集合以及距离矩阵
anchors_n_t = anchors_n_t + 1;
anchors(anchors_n_t) = j;
Locate=find(all == j);
all(Locate) = [];
for m = 1:culunm_road(1)
if(Data_road(m,1) == j)
matrix(Data_road(m,1),Data_road(m,2)) = Data_road(m,3);
elseif(Data_road(m,2) == j)
matrix(Data_road(m,2),Data_road(m,1)) = Data_road(m,3);
end
end
第五步:计算误差,输出结果
4.2 DV-HOP算法
第一步:将数据读入内存
利用Matlab中已有的函数load将文件中的内容以矩阵的方式读入内存。
第二步:判断锚节的个数
第三步:将所有的两点间的距离关系读入距离矩阵
for i =1:culunm_road(1)
matrix(Data_road(i,1),Data_road(i,2)) = Data_road(i,3);
matrix(Data_road(i,2),Data_road(i,1)) = Data_road(i,3);
end
shortest_path = matrix;
第四步:利用最短路径算法求得两点间的最短路径
for k=1:nodes_n
for i=1:nodes_n
for j=1:nodes_n
if shortest_path(i,k)+shortest_path(k,j)<shortest_path(i,j)
shortest_path(i,j) = shortest_path(i,k)+shortest_path(k,j);
jump_n(i,j) = jump_n(k,j);
end
end
end
End
第五步:求每个信标节点的校正值
利用函数:
anchor_to_anchor=shortest_path(1:anchors_n,1:anchors_n);
for i=1:anchors_n
hopsize(i)=sum(sqrt(sum(transpose((repmat(true(i,:),anchors_n,1)...
- true(1:anchors_n,:)).^2))))/sum(anchor_to_anchor(i,:));
End
第六步:未知节点计算位置
先通过距离=跳数*校正值求得未知节点到每个锚节点的距离,再根据最小二乘法计算具体位置。
obtained_hopsize=hopsize(find(shortest_path(i,1:anchors_n)==...
min(shortest_path(i,1:anchors_n)))); unknown_to_anchors_dist=transpose(obtained_hopsize(1)*...
shortest_path(i,1:anchors_n));
A=2*(estimated(1:anchors_n-1,:)-repmat(estimated(anchors_n,:),...
anchors_n-1,1));
anchors_location_square=transpose(sum(transpose...
(estimated(1:anchors_n,:).^2)));
dist_square=unknown_to_anchors_dist.^2;
b=anchors_location_square(1:anchors_n -1)-...
anchors_location_square(anchors_n)-dist_square(1:anchors_n-1)+..
dist_square(anchors_n);
estimated(i,:)=transpose(A\b);
第七步:计算误差,输出结果
5.实验结果和分析
5.1 迭代多边定位算法
1、实验结果
(1)无扰动值时的迭代多边定位算法
说明:红色圆圈表示节点实际位置,蓝色圆点表示利用迭代多边定位算法的估计位置。
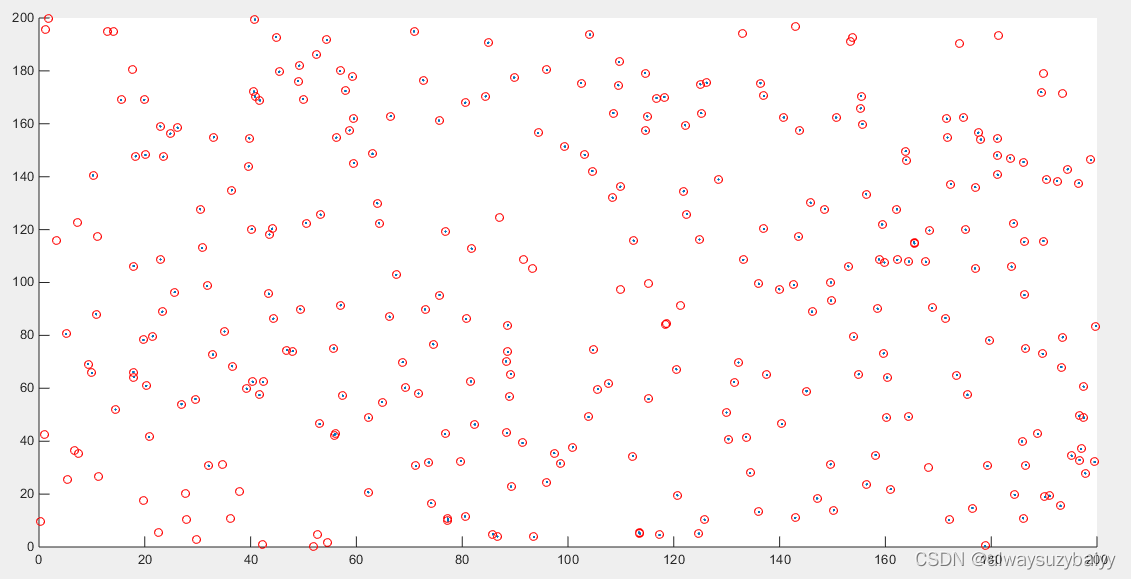
(2)5%误差扰动值时的迭代多边定位算法
说明:红色圆圈表示节点实际位置,蓝色圆点表示利用迭代多边定位算法的估计位置,蓝色连线表示某个节点实际位置与估计位置的误差。
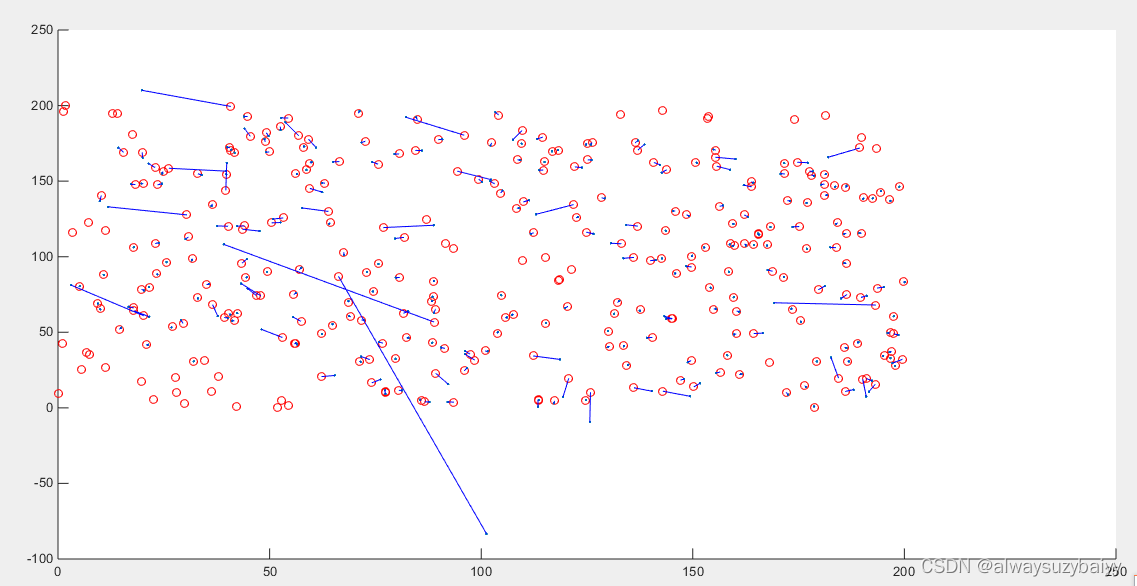
(3)10%误差扰动值时的迭代多边定位算法
说明:红色圆圈表示节点实际位置,蓝色圆点表示利用迭代多边定位算法的估计位置,黄色连线表示某个节点实际位置与估计位置的误差。
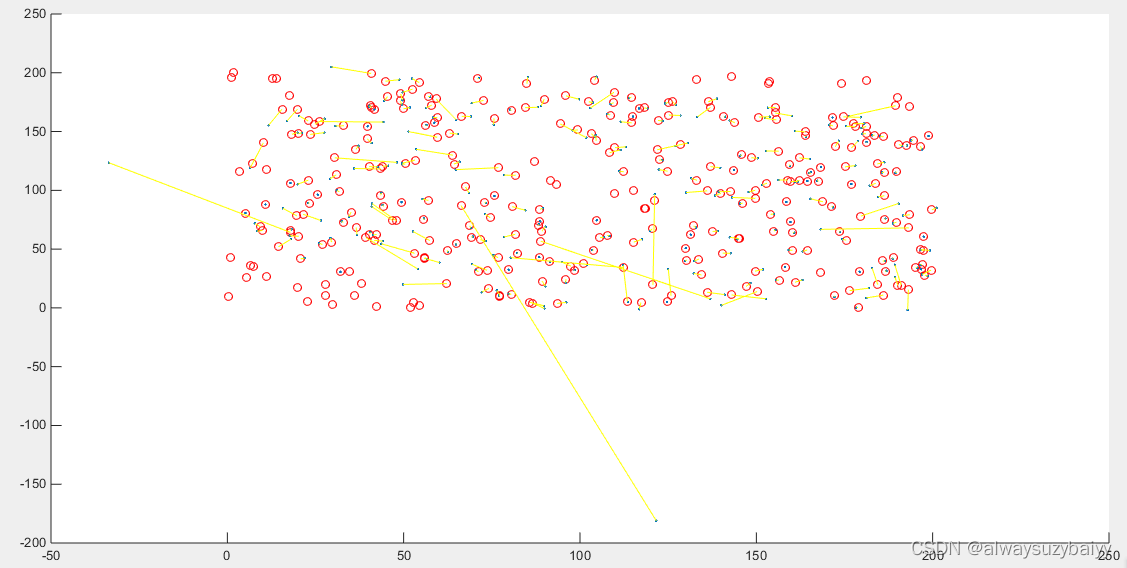
2、误差分析
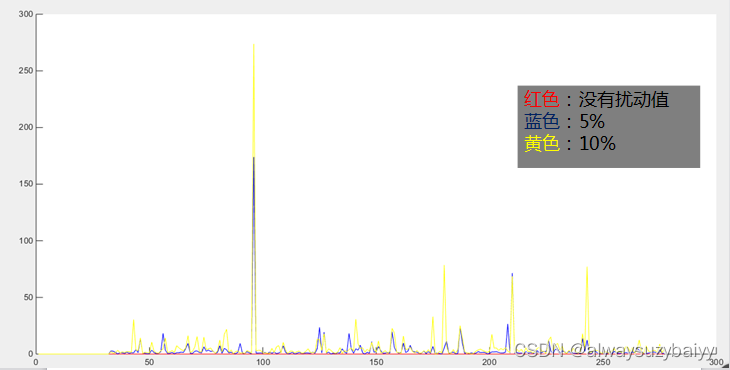
三次定位中,误差(方差)分别为:0.00034774693255881、3.12382496620916、5.57479034010724。
可以看出,随着扰动比例的不断提高,该算法的定位精准度在不断下降。这是由于迭代多边定位算法是通过取N和圆的交点来进行定位的,一旦出现了扰动,将改变两点间的距离,使得用于定位的部分圆半径不正确,出现定位不准确或定位点不合实际的情况。
5.2DV-HOP算法
1、实验结果
说明:蓝色“*”表示已知点的数据,红色圆点表示无扰动值时估计数据,蓝色圆点表示5%扰动值时估计数据,黄色圆点表示10%扰动值时估计数据,连线表示误差情况。
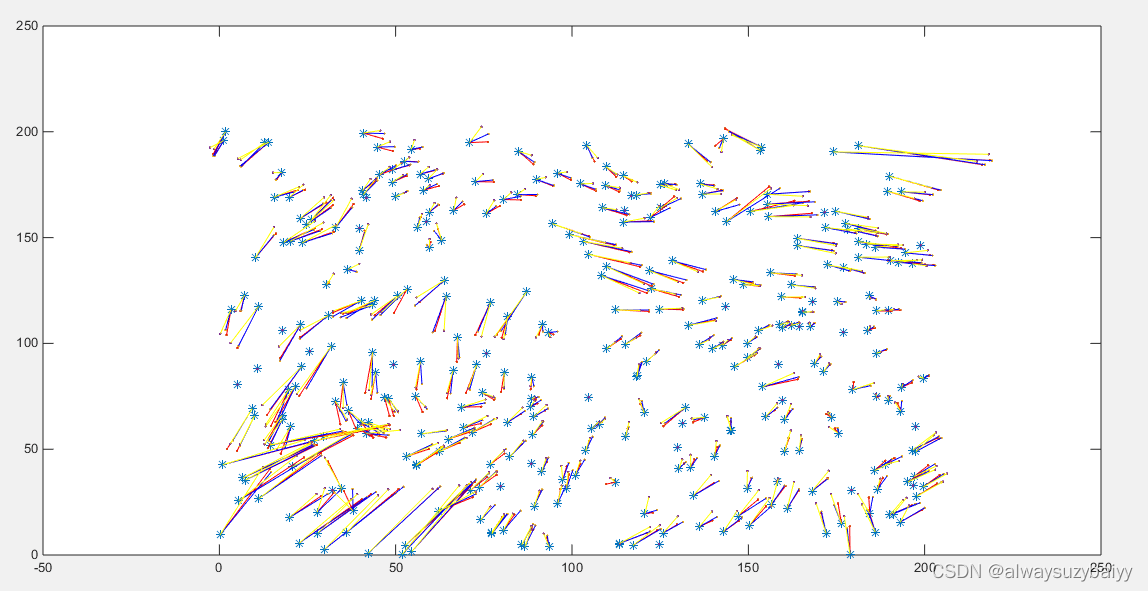
2、误差分析
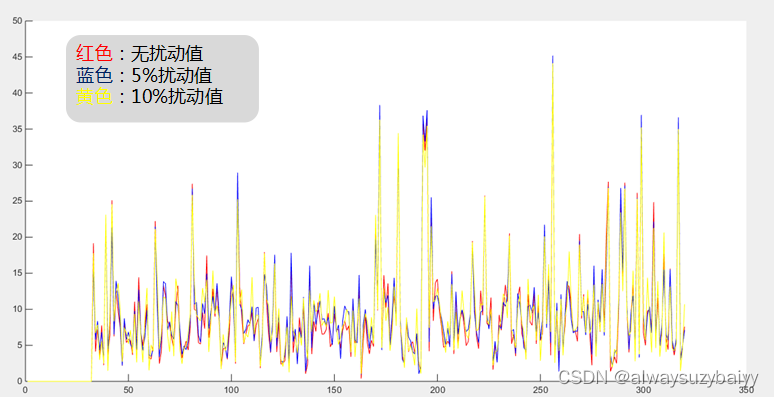
三次定位中,误差(方差)分别为:8.37509461994741、8.68160286181840、8.64112751102005。
可以看出,DV-HOP在有扰动值的情况下误差变化不大,但是定位也不是很准确,误差在1以内的点极少,几乎每个点都存在误差。