传送门

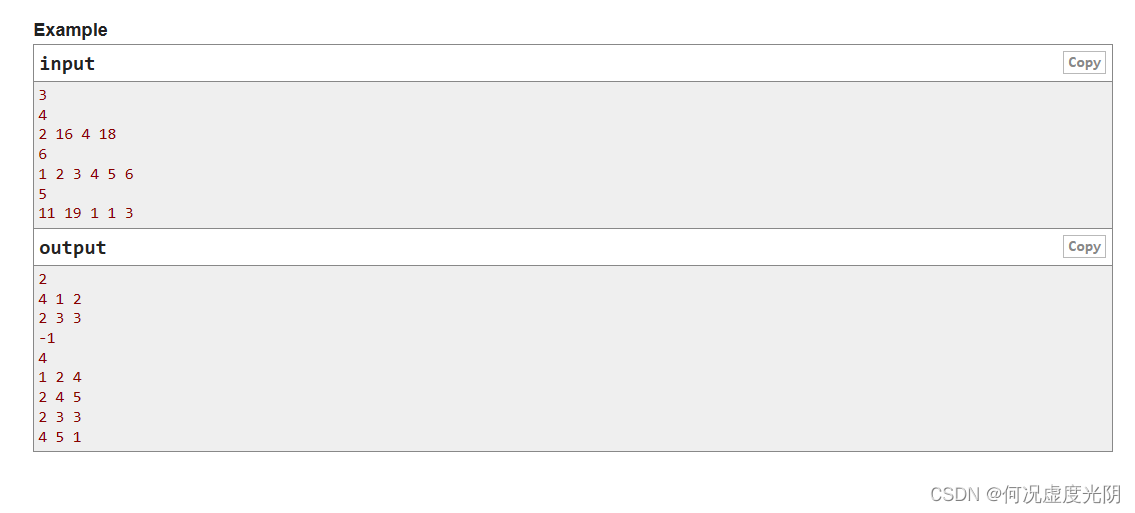
题意：

思路：

首先判断是否能够操作达到目的：即所有的数都相等。

不能达到有两种情况：

        1：所有数之和对n取余不等于0

        2:   每个ai都是小于i的，例如n=5, a[]={0,1,2,3,4}。因为每个数都是小于 i 的，所以不能进行有效操作。

以上是输出-1的情况。

然后：操作次数是需要考虑的，也就是每个ai最多操作3次。，所以我们让所有除了a1的数都进行3次操作。如果不需要操作，我们就输出无关的操作，废物操作。也就是操作后转移0,例如：4 1 0，5 1 0，这种的。

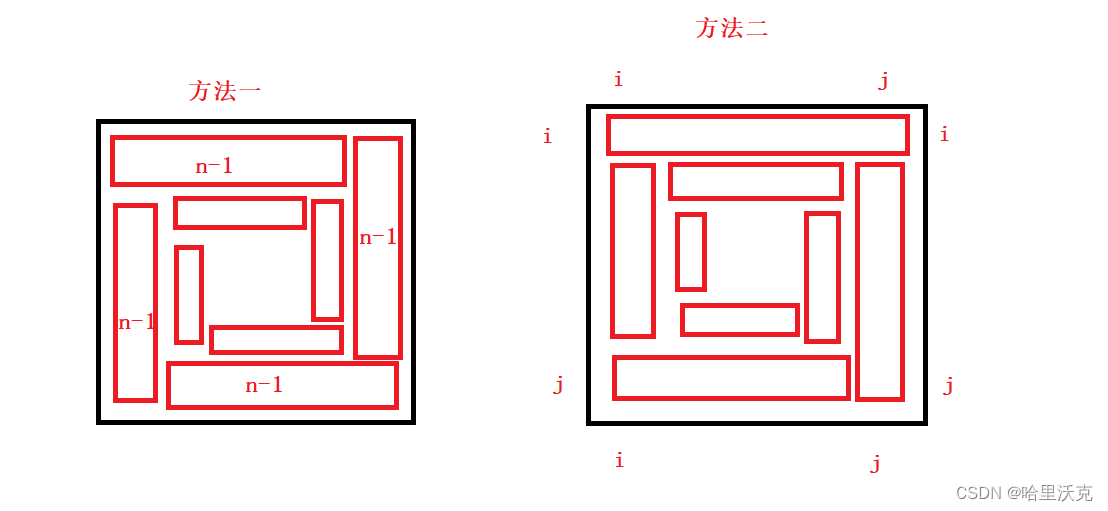
大致想一下，我们可以把所有的数全部转移到a[1]。然后最后把a1向ai进行操作就行了。

        如果一个,那么只需要一次操作就能全部转移到a1。然后添加一个无关操作(1,1,0)。

        如果,那么我们先让a1对ai进行补数，达到，这样包含一个操作，然后再进行操作：把ai转移到a1。 

这样最后达到了数组是 {sum,0,0,0...};

然后对每个ai进行补数（sum/n）,就行了。这样会发现刚好凑成了（n-1）*3次操作。

AC代码：

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+10; 
int a[N];
void solve(){
	int n;
	cin>>n;
	int sum=0;
	int flag=0;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		sum+=a[i];
		if(a[i]>=i){
			flag=1;
		}
	}
	if(sum%n!=0||flag==0){
		cout<<"-1\n";
		return ;
	}
	int num=sum/n;
	int l=2,r=2;
	cout<<(n-1)*3<<"\n";
	while(r<=n){
		if(a[r]%r==0){
			cout<<1<<" "<<1<<" 0"<<"\n";
		}
		else {
			cout<<"1 "<<r<<" "<<r-a[r]%r<<"\n";
			a[r]+=r-a[r]%r;
		}
		cout<<r<<" 1 "<<a[r]/r<<"\n"; 
		a[1]+=a[r];
		r++;
	}
	int ll=2;
	while(ll<=n){
		cout<<"1 "<<ll<<" "<<num<<"\n";
		ll++;
	}
}
signed main(){
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	int t;
	t=1;
	cin>>t;
	while(t--){
		solve();
	}
}