1.左右指针比大小

 977. 有序数组的平方

class Solution {
public:
    vector<int> sortedSquares(vector<int>& nums) {
        vector<int> ret = nums;
        int left = 0;
        int right = nums.size()-1;
        int end = nums.size();
        while(left<=right)
        {
            if(abs(nums[left])>abs(nums[right]))
            {
                ret[--end]=nums[left]*nums[left];
                left++;
            }
            else
            {
                ret[--end]=nums[right]*nums[right];
                right--;
            }
        }
        return ret;
    }
};

1.由于其数组本身的特性，两边的绝对值大，中间的小；说明其实数组可以由两边向中间走

2.由此，我们想到了左右指针，不过在遍历时要确定区间范围

3.定义一个vector ret存储平方数

3.比较哪个的绝对值大，哪个就被去拿去填入ret的左边往右边位置

2.滑动窗口

209. 长度最小的子数组

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        int sum=0;
        int ret = nums.size()+1;
        for(int i=0;i<nums.size();i++)
        {
            for(int j=i;j<nums.size();j++)
            {
                sum = 0;
                for(int k=i;k<=j;k++)
                {
                    sum+=nums[k];
                }
                if(sum>=target&&ret>(j-i+1))
                {
                    ret=j-i+1;
                }
            }
        }
        if(ret==(nums.size()+1))
            return 0;
        return ret;
    }
};

1.两层循环嘛，最简单的暴力遍历，非说要哪里注意的话，也就sum记得在每次重新开始前置为零

2.不过，这个代码leedcode跑不过，原因就是太暴力了，O(N^2)的时间复杂度不过呢

3.仔细分析一下为什么我们浪费了这么多的时间：仔细想想其实很简单，就是我们站得角度是顺序思考的，不就是求解嘛，一个一个对过去，这种思想使得我们不需要考虑直接暴力遍历；此时我们需要逆转一下思维（異議あり！，不好意思幽默一下），如果我们站在已经得到某个数组的条件满足要求，那么我们只需要去判断到底怎么样更小就行

转个场~

 滑动窗口

思想：

1.我们是通过两个下标i和j确定区间的，但是我们首先要做的不再是遍历去凑满足大于等于target的数组；而是先去得到一个满足要求的区间比较大的数组，随后去减小其区间更新返回值

2.因为说先得到个满足要求区间比较大的数组，所以i不动，j先往前，sum得到大于等于target，返回区间，随后走i，找到这么个比较大的数组里适合的最小区间。随后j继续往前走，i根据sum是否还满足要求在进行缩减

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        int sum = 0;
        int ret = nums.size()+1;
        int i = 0;
        for(int j=0;j<nums.size();j++)
        {
            sum+=nums[j];
            while(sum>=target)
            {
                if(ret>(j-i+1))
                {
                    ret=(j-i+1);
                }
                sum-=nums[i++];
            }
        }
        if (ret == (nums.size() + 1))
            return 0;
        return ret;
    }
};

分析：

这个的时间复杂度是O(N)，因为j了全长，限制了其量级，就算i也走完了全长，也就是N->2N而已。

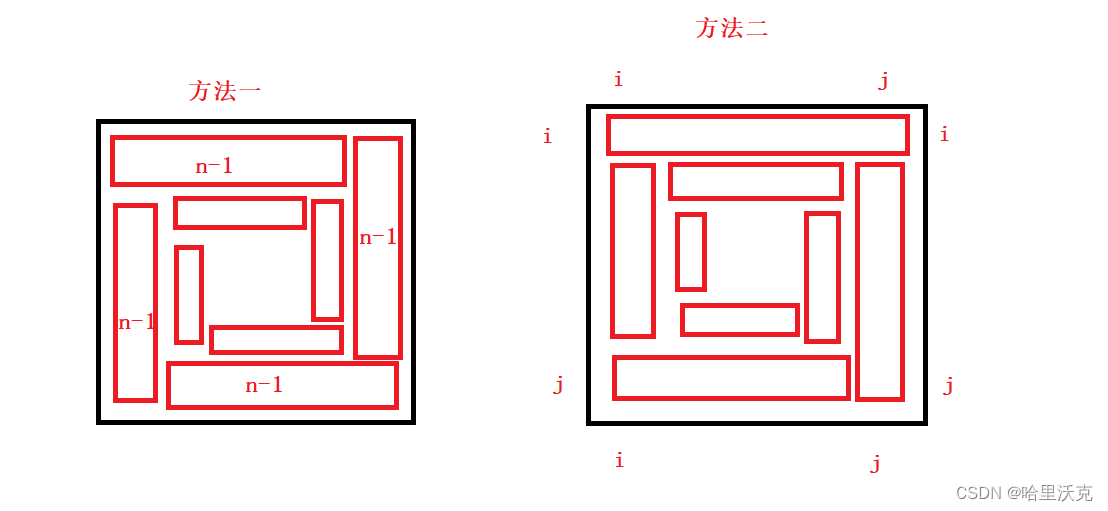
3.讨厌的循环

59. 螺旋矩阵 II

c++这个vector<vector<int>>我构造了十来分钟，烦得很。

注意是：vector<vector<int>> ret(n, vector<int>(n, 0))

它不像数组弄个[]就能出来，需要去调用构造函数，个数和需要的数据构造

这里两个方法都可以，不过后面那个的i和j更需要看范围

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        int i = 0;
        int j = n-1;
        int k = 0;
        int num = 0;
        vector<vector<int>> ret(n, vector<int>(n, 0));
        while(i<=j)
        {
            k=i;
            while(k<=j-1)
                ret[i][k++]=(++num);
            k=i;
            while(k<=j-1)
                ret[k++][j]=(++num);
            k=j;
            while(k>=i+1)
                ret[j][k--]=(++num);
            k=j;
            while(k>=i+1)
                ret[k--][i]=(++num);
            i++;
            j--;
        }
        if(n%2==1)
        {
            ret[(n-1)/2][(n-1)/2]=(++num);
        }
        return ret;
    }
};