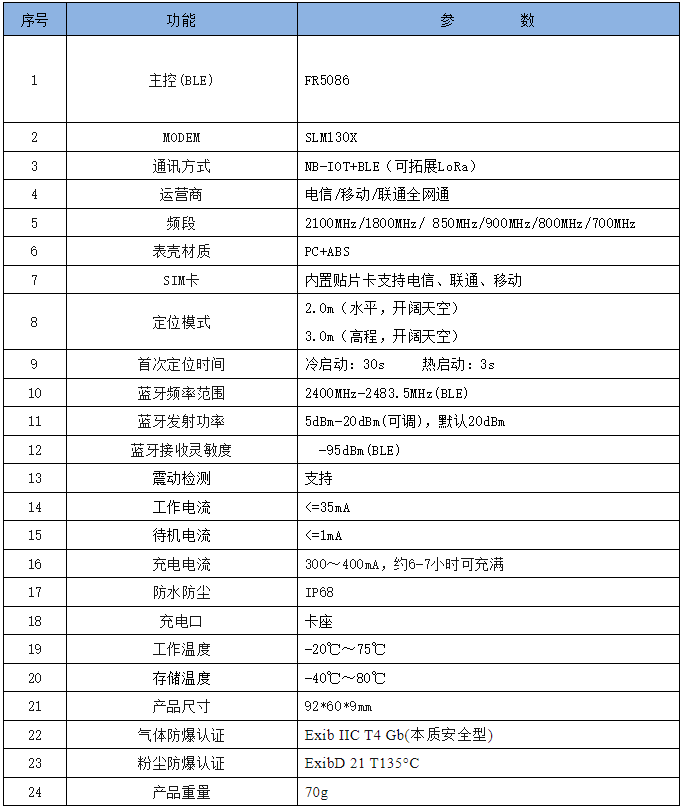
本系列文章主要是我在学习《数值优化》过程中的一些笔记和相关思考,主要的学习资料是深蓝学院的课程《机器人中的数值优化》和高立编著的《数值最优化方法》等,本系列文章篇数较多,不定期更新,上半部分介绍无约束优化,下半部分介绍带约束的优化,中间会穿插一些路径规划方面的应用实例
三、凸函数的性质
(1)凸函数满足Jensen不等式,如下所示:
f ( θ x + ( 1 − θ ) y ) ≤ θ f ( x ) + ( 1 − θ ) f ( y ) \begin{aligned}f(\theta x+(1-\theta)y)\leq\theta f(x)+(1-\theta)f(y)\end{aligned} f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)

此外,若 f ( θ x + ( 1 − θ ) y ) \begin{aligned}f(\text{}\theta x+(1-\theta)y)\\ \end{aligned} f(θx+(1−θ)y)均小于 θ f ( x ) + ( 1 − θ ) f ( y ) \begin{aligned}\theta f(x)+(1-\theta)f(y)\end{aligned} θf(x)+(1−θ)f(y),则称为严格凸函数,若在某些位置处取等号,则称为一般凸函数,,若将Jensen不等式中的小于号换成大于号,则为凹函数,同样分严格凹函数和一般凹函数,如下图所示:$$$$

(2)可借助上方图来判断是否为凸函数
上方图即函数上方的区域,若函数中任意两点连线均位于其上方图内,则该函数为凸函数,否则为凹函数,如下图所示:

(3)凸函数具有凸子水平集
如下面左图所示的函数f(x),取水平线y=α,f(x)<=α部分对应的x集合,称为该凸函数的子水平集,凸函数的子水平集也是凸的,下面右图给出了一个二维的例子,其子水平集是图中橙色区域所示的位置。

值得注意的是,非凸函数的子水平集也可能是凸的,下图中左图的函数是非凸的拟凸函数,而其子水平集是凸的

(4)任意多个凸函数的和或者加权相加依然是凸函数 ,多个拟凸函数的和不一定是拟凸函数。所有的的范数,如1范数、2范数、无穷范数等都是凸函数(因为范数必然满足三角不等式,则Jensen不等式成立,必为凸函数)

(5)凸函数的解集也是凸的
(6)凸函数经过仿射变换后依然是凸函数
仿射变换就是把x乘以一个矩阵A,再加上一个向量b,如下所示,凸函数经过仿射变换后依然是凸函数(可通过满足Jensen不等式来证明),凸函数经过仿射变换后其上方图也是凸的。
f ( x ) → f ( A x + b ) \begin{align*}f(x)&\quad\text{→}\quad f(Ax+b)\end{align*} f(x)→f(Ax+b)

(7)凸函数具有逐点最大保持凸性
若定义g(x)为几个凸函数中的最大值,则g(x)也是凸的
g ( x ) = max i f i ( x ) g(x)=\max\limits_i f_i(x) g(x)=imaxfi(x)
一些运算可以用max函数来表示,如绝对值、无穷范数、最大特征值等,如下所示,其也是凸函数。

以下四个函数均为凸函数:

(8)一个可微的凸函数一定位于其任意一点的线性近似的上方

(9)凸函数梯度等于0的点,是局部最小值,同时也是全局最小值

(10)若一个光滑函数的Hessian矩阵是半正定的,即 ∇ 2 f ( x ) \begin{aligned}\nabla^2f(x)\end{aligned} ∇2f(x)>=0,则该函数是凸函数。此外,对于一个非凸光滑函数而言,在其局部极小值处的Hessian矩阵也是半正定的。

若 f ( x ) = x T Q x > = 0 f(x)=x^{\text{T}}Qx>=0 f(x)=xTQx>=0,仅在x等于0处取等号,则其为严格凸函数,仅有一个最小值,若在x不等于0处也可以取等号,则其为一般凸函数,存在多个最小值,如下图所示:

(11)强凸性
强凸性代表着一个函数凸的程度,或者说强度,若凸函数满足以下表达式,则该函数具有强凸性,其中m大于0
f ( y ) ≥ f ( x ) + ( y − x ) T ∇ f ( x ) + m 2 ∥ y − x ∥ 2 \begin{aligned}f(y)\geq f(x)+(y-x)^T\nabla f(x)+\frac{m}{2}\|y-x\|^2\end{aligned} f(y)≥f(x)+(y−x)T∇f(x)+2m∥y−x∥2
由上述的性质(8)可知, f ( y ) ≥ f ( x ) + ( y − x ) T ∇ f ( x ) \begin{aligned}f(y)\geq f(x)+(y-x)^T\nabla f(x)\end{aligned} f(y)≥f(x)+(y−x)T∇f(x)对于任意一个凸函数必然成立,强凸性对凸函数提出了更高的要求,即在线性近似的基础上,又叠加了一个二次函数 m 2 ∥ y − x ∥ 2 \dfrac{m}{2}\left\|y-x\right\|^2 2m∥y−x∥2,即若某个凸函数位于下图中的绿色曲线上方,则可以认为该凸函数具备强凸性。

进一步,若该函数的Hessian存在时,则下式成立,其中 λ min \lambda_{\text{min}} λmin代表最小特征值

可以这样理解,若一个Hessian存在的凸函数,它的Hessian矩阵是严格正定的,并且它的最小奇异值也是正的,则这个函数就是一个强凸的函数。
(12)Lipschitz常数
Lipschitz常数M满足下式,直观上可以理解为任意两点的梯度的差值不会比它们距离的M倍更大
∥ ∇ f ( x ) − ∇ f ( y ) ∥ ≤ M ∥ y − x ∥ \|\nabla f(x)-\nabla f(y)\|\leq M\|y-x\| ∥∇f(x)−∇f(y)∥≤M∥y−x∥
上式成立,则可进一步得到下式:
f ( y ) ≤ f ( x ) + ( y − x ) T ∇ f ( x ) + M 2 ∥ y − x ∥ 2 f(y)\leq f(x)+(y-x)^T\nabla f(x)+\dfrac M2\|y-x\|^2 f(y)≤f(x)+(y−x)T∇f(x)+2M∥y−x∥2
在性质(11)中,若凸函数具有强凸性,则其必然位于强凸性曲线的上面,即其存在下届,若该函数的Lipschitz常数也存在,则又找到了一个上界,此时,该凸函数位于这两条曲线的之间,这样就可以把一个函数凸的程度刻画出来。
进一步,若x是局部极小值,则 ∇ f ( x ) \nabla f(x) ∇f(x)=0,此时,这两个不等式变为下式:,其中m和M可以用来判别一个函数的条件数
f ( y ) − f ( x ⋆ ) ≥ m 2 ∥ y − x ⋆ ∥ 2 f ( y ) − f ( x ⋆ ) ≤ M 2 ∥ y − x ⋆ ∥ 2 f(y)-f(x^{\star})\geq\dfrac{m}{2}\left\|y-x^{\star}\right\|^2\quad\quad f(y)-f(x^{\star})\leq\dfrac{M}{2}\left\|y-x^{\star}\right\|^2 f(y)−f(x⋆)≥2m∥y−x⋆∥2f(y)−f(x⋆)≤2M∥y−x⋆∥2
(13)凸函数的条件数
对光滑函数而言,若它的Hessian矩阵存在,则对其进行奇异值分解(SVD),最大得奇异值除以最小的奇异值就是条件数;对于可导,但是不一定具有Hessian矩阵到的凸函数,M/m即为条件数;对于一般的不可微的凸函数,在局部极小值中获取等高线,等高线构成图形(近似椭圆或椭球)的长轴/短轴,即为条件数

条件数决定了我们在优化算法里面是否要利用函数的高阶信息,有些算法对于条件数很小时,收敛很快,但是条件数很大时,不能收敛的很快,此时需要利用函数的曲率信息来更快的收敛到极小值
(14)次微分(次梯度)
为分析不可微的凸函数的收敛性和高阶信息引入次微分,次微分即在给定凸函数上任意取一点,寻找它的包络线,若在该点处,可微,包络线可取该点的切线,若在该点处连续但不可微,它的包络线可能有多个,可以取左导数形成的切线,也可以取右导数形成的切线,或者位于这两条切线之间的任意一条切线也可以。
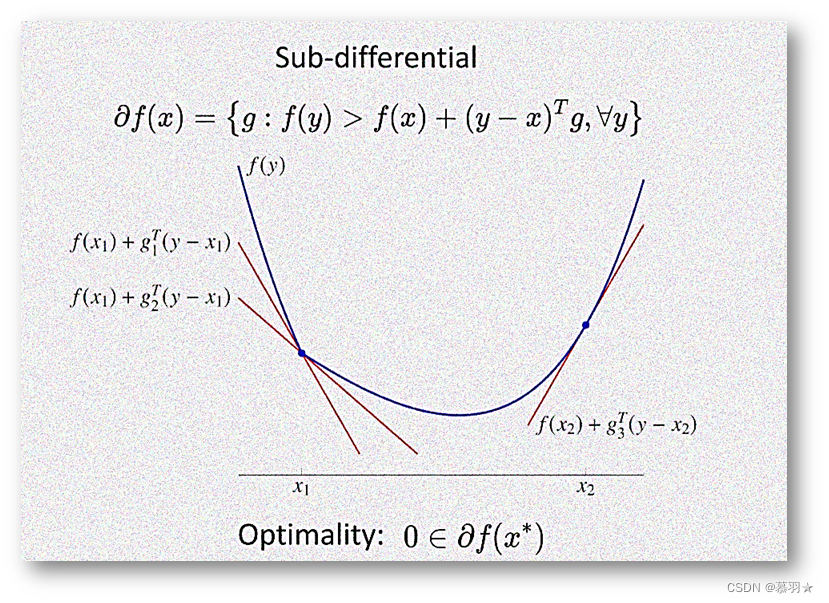
次微分(次梯度)就是包络的超平面,或者切线所构成的切平面所构成的斜率的集合。另外一种,我们可以定义一个函数的次梯度为方向导数的凸包,例如,凸函数在某点处不可导,左导数是g1,右导数是g2,则由g1和g2构成的凸包θ*g1+(1-θ)*g2称为函数在这个点处的次梯度。
函数的局部极小值处梯度为0,对于梯度不存在的点,判定一个点是否是最优的就是判断0是否属于这个点处次梯度的集合,如下图所示的绝对值函数在0点处微分不存在,其左导数是-1,右导数是1,则θ*-1+(1-θ)*1=1-2θ,其中θ属于0 ~ 1,则1-2θ的取值范围为-1 ~ 1,包含0,即绝对值函数在0这个点处的次梯度包含0元素,则0这个点是一个局部极小点,所以次微分的作用是用来判断一个点是否是不可微的凸函数一个极小值。

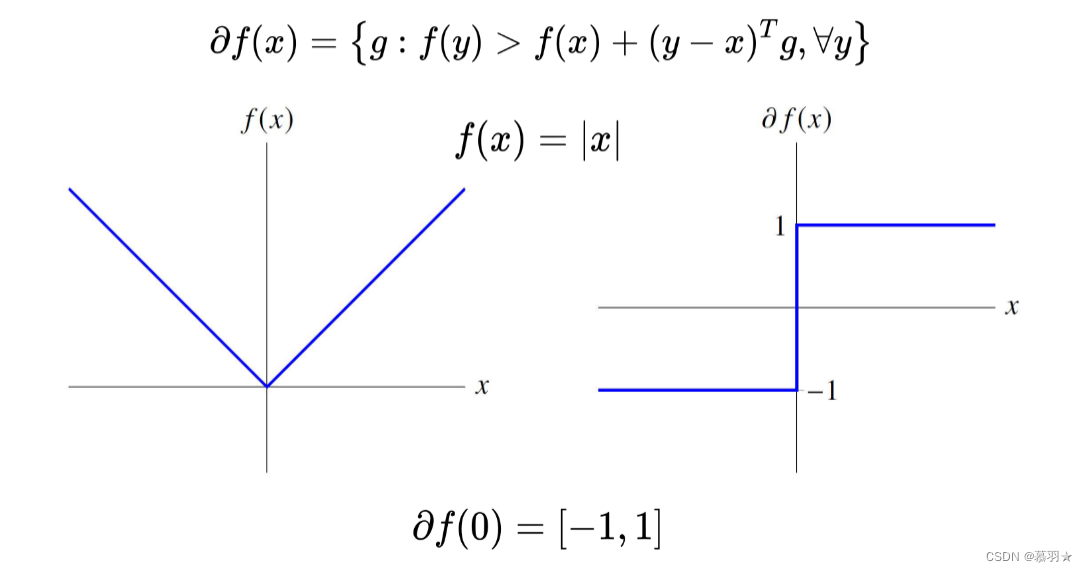
下图中第一个函数是凸的但不光滑的函数

下面的两个图分别对应上面两个图的俯视图,彩色线段是等高线,黑色箭头是沿着等高线的切线方向,在①处次微分是图中所绘制的三个红色向量的线性组合,包含0向量,因此,①处的点是一个局部极小点,在②处次微分是图中所绘制的两个红色向量的线性组合,不包含0向量,因此②处不是局部极小值点,同理可得,③处是局部极小值点,④处不是局部极小值点。

一般来说,如果一个函数是光滑的,沿着梯度的反方向走可以让函数值下降,但是对于一个非光滑的函数而言,并不是这样,沿着次微分(次梯度)的反方向走,不一定使得函数值下降,即负次微分方向不一定是下降方向 。
所以非光滑的函数对优化问题的求解带来一些困难,如果,我们知道我们求解问题的非光滑性来源于那些地方,大多数来源于拟合、max等,如果一个函数是分段光滑的,我们可以知道不光滑处位于分段的交界处。
对于非光滑的函数而言,最速下降的方向并不一定是梯度的反方向,因为,有时会不可微,不存在梯度,此时,最速下降方向一定是次梯度集合里面模长最小的那个向量的反方向。
(15)梯度单调性
对于凸函数而言,无论是可微。还是不可微,它们都有一种梯度单调性或者说,次梯度单调性的性质。任何凸函数的(次)梯度都是单调的。
对于可微的凸函数,梯度单调性表现为,任意两点y与x之差,以及它们在该处梯度之差的内积是大于等于0的,如下式所示:
⟨ y − x , ∇ f ( y ) − ∇ f ( x ) ⟩ ≥ 0 \langle y-x,\nabla f(y)-\nabla f(x)\rangle\geq0 ⟨y−x,∇f(y)−∇f(x)⟩≥0
同理,对于不可微的凸函数,则把上式中的梯度换成次梯度,如下式所示:
⟨ y − x , g y − g x ⟩ ≥ 0 , g x ∈ ∂ f ( x ) , g y ∈ ∂ f ( y ) \langle y-x,g_y-g_x\rangle\geq0,g_x\in\partial f(x),g_y\in\partial f(y) ⟨y−x,gy−gx⟩≥0,gx∈∂f(x),gy∈∂f(y)
参考资料:
1、机器人中的数值优化