2023/4/16周报

摘要

论文阅读

1、标题和现存问题

2、模型构建

3、方法实现

4、实验结果

5、扩展实验

深度学习

1、GNN特点

2、原理

3、GNN数据处理

总结

摘要

本周在论文阅读上，阅读了一篇基于图神经网络的技术识别链接预测方研究论文。通过融合了时间特征的专利IPC共现网络，训练图神经网络模型实现链接预测方法，为技术发现和知识供给提供参考。但文章模型对于运算成本和时间成本较其他模型需求更高，这是以后应当进行优化的方向。在深度学习上，复习了GNN的特点和原理，同时对GNN的数据集制作也进行了学习。

This week,in terms of thesis reading,perusaling a research paper on graph neural network-based technology for identifying link predictors.By using a patent IPC co-occurrence network that integrates temporal features, a graph neural network model is trained to implement link prediction methods, providing reference for technology discovery and knowledge supply.However, the article model has higher requirements for computational and time costs compared to other models, which should be optimized in the future.In deep learning,reviewing the characteristics and principles of GNN, as well as also learning about the production of GNN datasets.

论文阅读

1、标题和现存问题

标题：基于图神经网络的技术识别链接预测方研究

现存问题：现有的链接预测方法可以分为基于相似性和基于学习的方法。在基于相似性链接预测方法上存在依赖相似性度量、不适用于大规模网络、无法处理缺失数据等问题；在基于学习链接预测方法上存在需要大量数据和计算资源、可能存在过拟合问题、模型解释性较差等问题。

2、模型构建

GCN其卷积思想主要体现在节点之间的信息共享，每一层都共享卷积核参数，但是如果只有一阶共享，也就意味着节点只收到了它周围一阶邻居的影响，因此可以继续叠加K层图卷积层，从而扩大远方邻居的影响力，聚合函数公式：

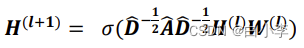
在GCN模型中，节点的属性信息和结构信息同时进行训练和学习的，二者具有良好的互补关系，能够协同影响节点的表示。但GCN本身是“直推式学习”，只能学习当前数据，无法做到灵活泛化，因此提出了 GraphSAGE（“归纳式学习”模型）来进行邻居采样和归纳式学习。其中包含2个步骤Sample（邻居采样）和 Aggregate（信息聚合）。在采样环节，先得到节点的K阶邻居集合，在对邻居采样时只均匀采样固定数量的邻居节点；在聚合环节，每次迭代搜索时只学习信息聚合函数，由远到近聚合邻居节点的信息。经过采样和聚合得到的节点嵌入向量再作为输入送入下游的其他任务。

文章将时间特征作为节点的属性纳入图神经网络训练，并参与到后续的邻居信息聚合当中，时间关注度是基于心理学领域遗忘曲线所表示的偏好保持，研究提出记忆和遗忘变化是呈指数形式的变化，且遗忘先快后慢。记忆量的保持函数：

IPC 的时间关注度公式：

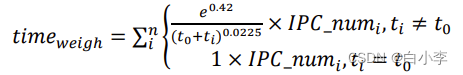
IPC 的时间稳定性公式（方差越小，稳定性越高，）：

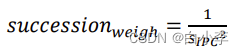
3、方法实现

文章的研究数据来自Incopat专利数据库

首先随机抽取数据集中已经存在的边，即IPC组合对，作为测试集中的正样本，之后负采样生成相同数量的负样本，将正负样本合并划分训练集和测试集，使得训练集和测试集中的正负样本比例为1:1，初始设置训练集80%，测试集10%，验证集10%。

在图神经网络的搭建过程中，主要有节点表示和链接表示两个模块。在进行节点表示时需要经历邻居采样和信息聚合两个阶段。在邻居采样过程中，设置超参数 K，即节点采样的K阶邻居，即定义K层GrapSAGE。当得到各个节点的表示之后就需要对两点之间的链接即组合来进行表示，该表示可以认为是两节点未来存在链接的概率得分。

在得到节点和链接的表示后设置激活函数、损失函数和优化器对链接预测模型进行训练，实验过程中在前向传播时选用ReLU为激活函数，采用Adam优化器，学习率设为0.01，以交叉熵作为损失函数进行反向传播训练。

文章采用AUC来评估基于GNN的链接预测模型效果。AUC指标常作为衡量二分类算法整体准确度的指标，它的含义是二分类中，给定正负两个样本，正样本判定为正比将负样本判定为正大的概率值。AUC指标结果越高，表明模型表现的效果越好。

4、实验结果

下面表示Dot_Predictor和MLP_Predictor采用mean、pool和lstm三种不同的信息聚合函数时在不同的节点表示维度上的实验效果。在相同的维度下，采用不同得分预测的函数情况下，均值聚合的效果总要优于池化聚合和LSTM聚合。相比来说，当在相同向量维度下，相同聚合函数采用MLP_Predictor预测得分的效果要显著优于Dot_Predictor得分预测函数，因此文章将采用12维向量表示IPC节点，在邻居信息聚合过程中使用均值函数计算目标节点的表示，最后采用自定义的 MLP_Predictor来对IPC节点组合之间的链接进行预测，并将其与其他模型进行对比分析。

文章选择的基线模型是在链接预测领域比较经典的基于节点相似性的计算方法，在以往的链接预测研究中应用甚广，分别为AA指标、CN指标、Jaccard系数、PA指标、RA指标，除此外，基线模型还包括学习节点路径特征的图游走算法Node2Vec。选择ANN作为Node2Vec的相对较优模型进行后续的对比分析。

选定相对较优后对各个模型的效果做整体比较分析，其中为了得到可信的实验结果，通过改变训练集的比例，即训练集分别占比60%、65%、70%、75%、80%、85%、90%进行多次实验来验证实验的效果，具体数值下表所示。

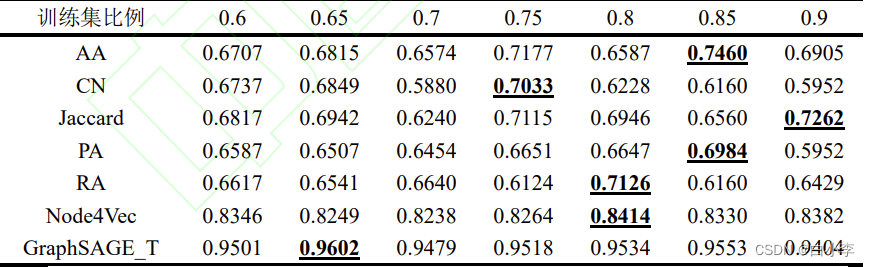
相对于各基线模型的最优实验结果，基于图神经网络的链接预测结果分别提升了28.71%、36.52%、32.22%、37.48%、34.75%、14.11%，证实了该方法的可用性。

训练集占比对耗时影响-基线模型：

训练集占比对耗时影响-基线模型和 GraphSAGE_T：

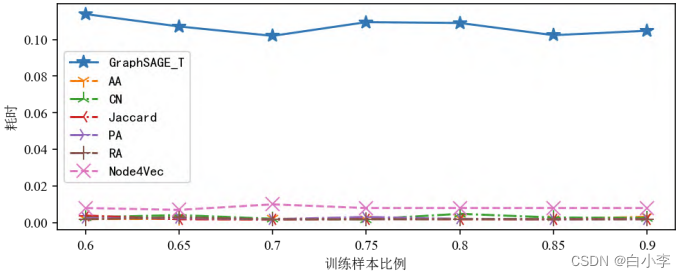
图神经网络的实验效果有明显优势，但其本质上是深度学习模型，在训练过程中涉及大量的数学运算，时间成本相对于其他模型也更高。在实际的链接预测任务当中，对于实时性要求不高的作业，图神经网络可以给出更加精确可信的结果，但对于实时性要求更强的任务则需要进行进一步的优化。

5、扩展实验

为了验证 GraphSAGE_T实验中的时间特征是否在节点表示和边预测的任务中都发挥了作用，本节采用此前实验的参数进行拓展实验，将仅剔除时间稳定性特征得到的模型记为GraphSAGE_ V1，将仅剔除时间关注度特征得到的模型记为 GraphSAGE_ V2，将仅剔除年份分布特征得到的模型记为GraphSAGE_ V3；将剔除所有时间特征得到的模型记为GraphSAGE_ V4。

可见当不考虑IPC的时间稳定性时，模型效果略有下降，相对于最优效果下降了 2.51%，当不考虑IPC的时间关注度时，下降 2.99%，当不考虑年份分布特征时，效果下降了 4.09%，当不考虑三个时间特征时，效果下降了 7.93%，较为明显，可见本文提出的在专利领域IPC的两个时间特征：时间关注度和时间稳定性会对其链接预测的效果产生一定的正向影响，同时专利IPC号的年度分布这一特征的重要性再一次得到了验证。

深度学习

1、GNN特点

特点：

图结构建模能力：GNN能够有效地处理图结构数据，包括节点之间的关系、图中的拓扑结构以及图中的属性信息。GNN可以对节点及其邻居的特征进行聚合和传递，从而能够在处理图数据时充分利用节点之间的关联信息。
上下文感知性：GNN可以通过节点之间的信息传递来捕捉节点的上下文信息。每个节点的表示是通过聚合其邻居节点的表示得到的，从而能够综合考虑节点的局部上下文。
可扩展性：GNN具有良好的可扩展性，可以应对大规模图数据。GNN通过局部聚合和信息传递的方式进行计算，可以在处理大型图数据时保持较低的计算和存储复杂度。
泛化能力：GNN可以对未见过的节点进行泛化，即在训练时学到的模型可以应用于未知的节点。这种泛化能力使得GNN在处理具有动态性和不完整性的图数据时具有优势

优点：

建模图结构能力强：GNN可以有效地处理图结构数据，包括节点之间的关系和属性信息，能够对图数据进行高效的表示学习和预测。
上下文感知性：GNN能够通过节点之间的信息传递捕捉节点的上下文信息，从而在处理图数据时能够考虑节点的局部上下文，具有较强的表征能力。
可扩展性：GNN在处理大规模图数据时具有较好的可扩展性，可以有效地处理复杂的图结构数据。
泛化能力：GNN在处理未见过的节点时具有泛化能力，即在训练时学到的模型可以应用于未知的节点，具有较强的适应性。

缺点：

计算复杂度高：GNN的计算复杂度通常较高，特别是对于大规模图数据和复杂的图结构，可能需要较大的计算资源。
超参数选择困难：GNN中包含一些超参数，如层数、隐藏单元数、学习率等，选择合适的超参数对于模型的性能至关重要，但选择合适的超参数可能会比较困难。
信息传递过程限制：GNN中的信息传递过程通常是局部的

GNN种类：

图卷积网络（Graph Convolutional Networks，GCN）: 是最早和最常见的GNN类型，采用卷积操作在图结构上进行信息传递和特征聚合，通过对节点和其邻居节点的特征进行卷积操作来生成节点的新特征表示。
图注意力网络（Graph Attention Networks，GAT）: 使用注意力机制（attention mechanism）来对节点的邻居节点进行加权聚合，从而使得节点能够更加灵活地选择邻居节点的信息，具有较强的自适应性。
图池化网络（Graph Pooling Networks）: 用于在处理图数据时进行图层间的下采样（downsampling）操作，通过对图中节点的聚合和采样来减少图的规模，从而降低计算复杂度。
图生成网络（Graph Generative Networks）: 用于生成新的图数据，包括图生成模型（Graph Generative Models）和图生成神经网络（Graph Generative Neural Networks），用于生成具有特定属性或拓扑结构的图。
时空图神经网络（Spatio-Temporal Graph Neural Networks）: 用于处理时空图数据，如时空社交网络、交通流量数据等，通过考虑图数据中的时序和空间关系来进行建模和预测。
异构图神经网络（Heterogeneous Graph Neural Networks）: 用于处理包含多种类型节点和边的异构图数据，如社交网络中的用户、商品和评论等不同类型节点的关系。
多层图神经网络（Multi-layer Graph Neural Networks）: 使用多层的GNN模型来进行多阶信息传递和特征抽取，从而能够对更复杂的图结构进行建模。

2、原理

主要原理可以概括为以下几个步骤：

图数据表示：GNN首先对图数据进行节点和边的表示。通常使用向量或矩阵来表示节点特征，例如节点的属性、标签或位置等信息。边通常用矩阵或张量表示，描述节点之间的关系、连接或权重。
信息传递：GNN通过在图结构上进行信息传递和特征聚合，从而将节点的特征信息与其邻居节点的特征信息进行交互。这通常通过局部聚合规则来实现，例如通过卷积、池化、注意力等操作，将节点自身的特征与邻居节点的特征进行融合。
特征更新：GNN通过信息传递和特征聚合操作更新节点的特征表示。通常，更新规则会根据节点自身的特征和邻居节点的特征来计算节点的新特征表示。这一过程可以进行多轮迭代，使节点的特征逐步演化。
输出预测：GNN可以在图中的节点或边上进行预测，例如节点分类、边预测、图分类等任务。通常，GNN会使用节点的最终特征表示作为输入，通过一个或多个全连接层或其他输出层来生成预测结果。

GNN的原理可以看作是在图结构上进行信息传递和特征聚合，从而实现对图数据的建模和预测。这种方式允许GNN在处理非结构化、异构性和动态性的图数据时具有灵活性和强大的建模能力，并在许多实际应用中取得了显著的成功。

节点更新公式：用于更新节点的特征表示，可以表示为：

其中，h_{v}^{(l)}表示节点v在第l层的特征表示，f表示一个非线性激活函数，aggregate表示聚合函数，用于聚合节点v的邻居节点u在第l层的特征表示，N(v)表示节点v的邻居节点集合。

边更新公式：用于更新边的特征表示，可以表示为：

其中，e_{vw}^{(l)}表示边v和w在第l层的特征表示，g表示一个非线性激活函数。

节点/边的初始化公式：用于初始化节点/边的特征表示，通常为随机初始化或根据输入数据进行初始化。

输出层公式：用于生成最终的预测结果，可以根据具体任务而定，例如节点分类、边预测或图分类等。

3、GNN数据处理

图数据加载：首先，需要加载图数据，包括节点和边的信息。通常，图数据可以表示为一个邻接矩阵或者一个节点和边的列表。
节点特征表示：对于每个节点，需要将其特征表示为一个向量或者矩阵，作为输入传递给GNN模型。节点特征可以包括节点自身的属性，如节点的数值属性、文本属性等，也可以包括节点的邻居信息，如邻居节点的属性、边的属性等。
边特征表示：对于每条边，也需要将其特征表示为一个向量或者矩阵，作为输入传递给GNN模型。边特征可以包括边的属性，如边的权重、边的类型等。
图数据预处理：对加载的图数据进行预处理，包括数据归一化、特征缩放、处理缺失值等。这一步骤旨在将图数据转换为适合输入GNN模型的格式，并且确保数据的一致性和合理性。
GNN模型输入构建：将节点特征和边特征组合成输入数据，构建GNN模型的输入。通常，输入可以表示为一个节点特征矩阵和一个边特征矩阵，或者通过邻接矩阵和节点特征矩阵表示。
GNN模型训练：使用构建好的输入数据，将其输入到GNN模型中进行训练。在训练过程中，GNN模型通过节点之间的信息传递和特征更新来学习节点的表示，并最终输出预测结果。
模型评估和调优：训练完成后，需要对GNN模型进行评估和调优，包括使用验证集和测试集进行性能评估，根据评估结果进行模型调优，如调整超参数、修改网络结构等。

图数据表示是将图中的节点和边表示成适合输入到图神经网络（GNN）模型的格式。一般来说，图数据表示需要将节点和边的特征表示为向量或矩阵形式，以便GNN模型能够对其进行处理。

节点特征表示：节点特征通常包括节点的属性特征，如节点的数值属性、文本属性等。节点特征可以表示为向量或矩阵，其中每个维度对应一个特征。例如，可以使用one-hot编码表示离散属性，使用实数向量表示连续属性。对于文本属性，可以使用词嵌入（word embeddings）或其他文本表示方法将文本转换成固定维度的向量表示。

边特征表示：边特征通常包括边的属性特征，如边的权重、边的类型等。边特征也可以表示为向量或矩阵，其中每个维度对应一个特征。例如，可以使用实数向量表示边的权重，使用二进制编码表示边的类型。

在图神经网络（GNN）中，邻接矩阵（Adjacency Matrix）是一种常用的表示图结构的方式。它是一个方阵，用于表示图中节点之间的连接关系。邻接矩阵的形式可以是二进制矩阵或带权重的矩阵，取决于图中节点之间的连接方式。对于无向图，邻接矩阵一般是对称矩阵，因为边没有方向；对于有向图，邻接矩阵则可能不是对称矩阵，因为边有方向。假设有 N 个节点的图，那么邻接矩阵 A 的维度为 N × N。其中 Ai 表示节点 i 到节点 j 之间是否存在边，或者边的权重（如果有权重的话）。通常情况下，Ai 的取值为 0 或 1，表示没有边或有边的存在。如果图中存在带权重的边，则 Ai 的取值可以是边的权重值。

import numpy as np

# 创建一个无向图的邻接矩阵
num_nodes = 5
adj_matrix = np.zeros((num_nodes, num_nodes), dtype=int)

# 添加边
edges = [(0, 1), (1, 2), (2, 3), (3, 4), (4, 0)]
for edge in edges:
    adj_matrix[edge[0]][edge[1]] = 1
    adj_matrix[edge[1]][edge[0]] = 1

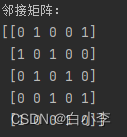
print("邻接矩阵：")
print(adj_matrix)

这段代码创建了一个包含 5 个节点的无向图，其中节点 0 到节点 1、节点 1 到节点 2、节点 2 到节点 3、节点 3 到节点 4、节点 4 到节点 0 都存在边连接。邻接矩阵 adj_matrix 就表示了这个图的连接关系，其中的 1 表示节点之间存在边的连接，0 表示节点之间没有边连接。