( “树” 之 BST) 669. 修剪二叉搜索树 —

( “树” 之 BST) 669. 修剪二叉搜索树 ——【Leetcode每日一题】

news2024/9/29 5:37:50

二叉查找树（BST）：根节点大于等于左子树所有节点，小于等于右子树所有节点。
二叉查找树中序遍历有序。

669. 修剪二叉搜索树

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。可以证明，存在 唯一的答案 。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

示例 1：

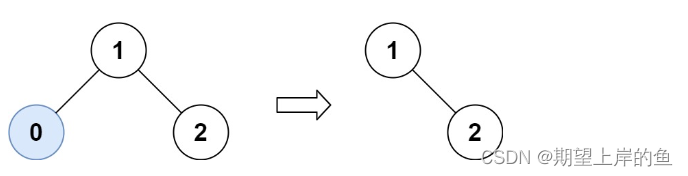
在这里插入图片描述

输入：root = [1,0,2], low = 1, high = 2
输出：[1,null,2]

示例 2：

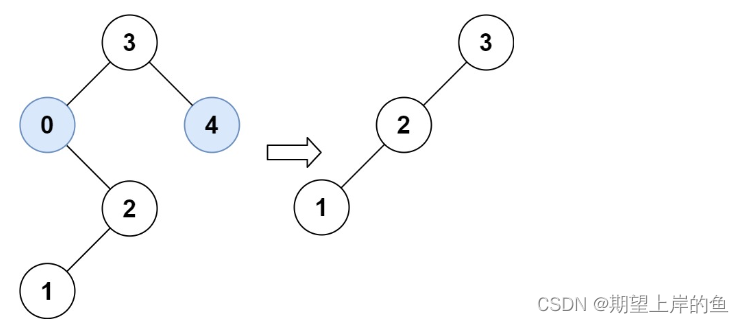
在这里插入图片描述

输入：root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出：[3,2,null,1]

提示：

树中节点数在范围 $1, 10^4]$ 内
$0 <= Node.val <= 10^4$
树中每个节点的值都是唯一的
题目数据保证输入是一棵有效的二叉搜索树
$0 <= low <= high <= 10^4$

思路：

法一：递归：

任意一个节点的val，对给定的范围只有三种可能，等于、小于、大于

等于：也就在给定的范围内，则保留，再分别判断该节点的左子树和右子树；
小于：当该节点小于给定范围的最小值时，要将该节点以及该节点的左子树都修剪掉，让该节点的父节点的左指针指向该节点的右子树，再进行判断；
大于：当该节点大于给定范围的最大值时，要将该节点以及该节点的右子树都修剪掉，让该节点的父节点的右指针指向该节点的左子树，再进行判断；

法二：迭代：

该题自然能够使用「迭代」进行求解：起始先从给定的 root 进行出发，找到第一个满足值符合 [low,high]范围的节点，该节点为最后要返回的真正的根节点 root。

然后分别处理root节点的左子树和右子树：

这里对左子树，只需修剪掉小于所给范围的节点；
- 若节点大于给定范围的最小值时，这该节点的右子树一定在范围内，不修剪，继续判断其左子树；
- 若节点小于给定范围的最小值时，要将该节点以及该节点的左子树都修剪掉，让该节点的父节点的左指针指向该节点的右子树，再进行判断。
而对右子树只需修剪掉大于所给范围的节点;
- 若节点小于给定范围的最大值时，这该节点的左子树一定在范围内，不修剪，继续判断其左子树；
- 若节点大于给定范围的最大值时，要将该节点以及该节点的右子树都修剪掉，让该节点的父节点的右指针指向该节点的左子树，再进行判断。

代码：(Java、C++)

法一：递归：
Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        if(root == null) return null;
        if(root.val >= low && root.val <= high){
            root.left = trimBST(root.left, low, high);
            root.right = trimBST(root.right, low, high);
        }else if(root.val < low){
            return trimBST(root.right, low, high);
        }else if(root.val > high){
            return trimBST(root.left, low, high);
        }
        return root;
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if(root == nullptr) return nullptr;
        if(root->val >= low && root->val <= high){
            root->left = trimBST(root->left, low, high);
            root->right = trimBST(root->right, low, high);
        }else if(root->val < low){
            return trimBST(root->right, low, high);
        }else if(root->val > high){
            return trimBST(root->left, low, high);
        }
        return root;
    }
};

法二：迭代：
Java

class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
       while(root != null && (root.val < low || root.val > high)){
           root = root.val < low ? root.right : root.left;
       }
       if(root == null) return null;
       TreeNode tem = root;
       while(tem.left != null){
           if(tem.left.val >= low){
               tem = tem.left;
           }else{
               tem.left = tem.left.right;
           }
       }
       tem = root;
       while(tem.right != null){
           if(tem.right.val <= high){
               tem = tem.right;
           }else{
               tem.right = tem.right.left;
           }
       }
       return root;
    }
}

C++

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        while(root != nullptr && (root->val < low || root->val > high)){
           root = root->val < low ? root->right : root->left;
       }
       if(root == nullptr) return nullptr;
       TreeNode* tem = root;
       while(tem->left != nullptr){
           if(tem->left->val >= low){
               tem = tem->left;
           }else{
               tem->left = tem->left->right;
           }
       }
       tem = root;
       while(tem->right != nullptr){
           if(tem->right->val <= high){
               tem = tem->right;
           }else{
               tem->right = tem->right->left;
           }
       }
       return root;
    }
};