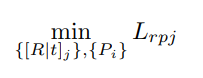问:已知三维空间中的两个样本点分别为(2,4,5)和(1,2,3),定义核函数表达式为:
试计算这两个样本点映射到十维空间后的
![]()
答:首先计算两个样本点的平方内积=2*1+4*2+5*3=25
然后代入核函数表达式:25*5+6=131
1.核函数把低维空间映射到高维空间
下面这张图位于第一、二象限内。我们关注红色的门,以及“北京四合院”这几个字下面的紫色的字母。我们把红色的门上的点看成是“+”数据,紫色字母上的点看成是“-”数据,它们的横、纵坐标是两个特征。显然,在这个二维空间内,“+”“-”两类数据不是线性可分的。

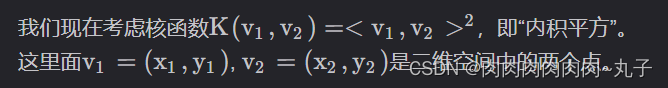
这个核函数对应着一个二维空间到三维空间的映射,它的表达式是:
在P这个映射下,原来二维空间中的图在三维空间中的像是这个样子: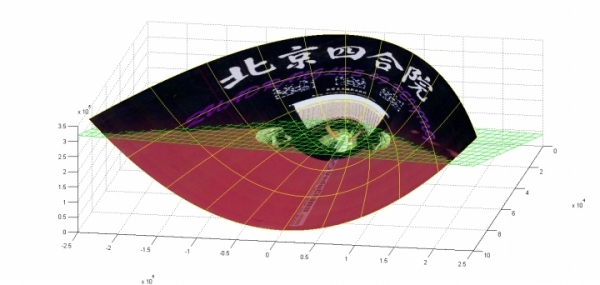
前后轴为x轴,左右轴为y轴,上下轴为z轴)
注意到绿色的平面可以完美地分割红色和紫色,也就是说,两类数据在三维空间中变成线性可分的了。
而三维中的这个判决边界,再映射回二维空间中是这样的:
这是一条双曲线,它不是线性的。
如上面的例子所说,核函数的作用就是隐含着一个从低维空间到高维空间的映射,而这个映射可以把低维空间中线性不可分的两类点变成线性可分的。当然,我举的这个具体例子强烈地依赖于数据在原始空间中的位置。事实中使用的核函数往往比这个例子复杂得多。它们对应的映射并不一定能够显式地表达出来;它们映射到的高维空间的维数也比我举的例子(三维)高得多,甚至是无穷维的。这样,就可以期待原来并不线性可分的两类点变成线性可分的了。
该映射的效果如下图所示:
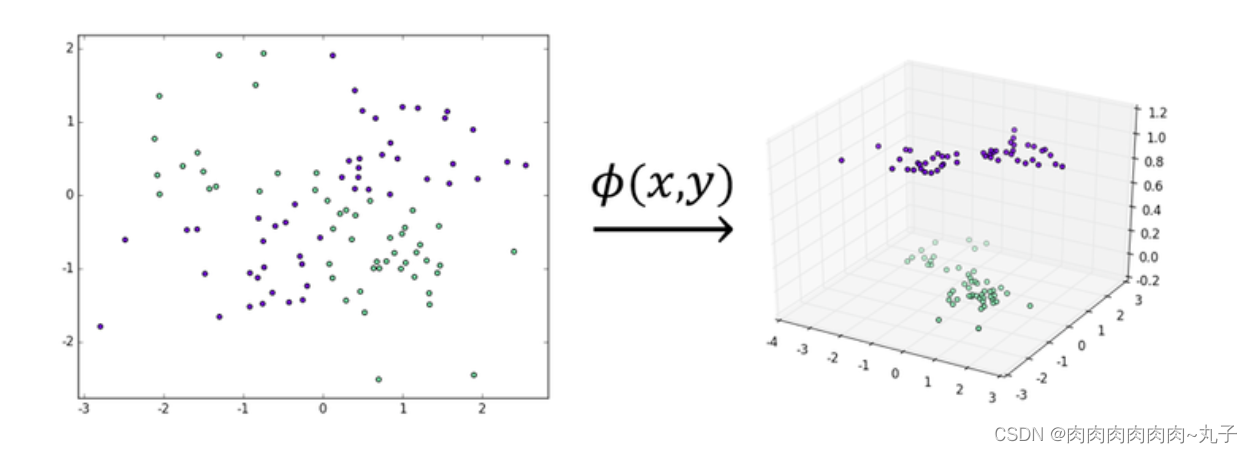

2.常见的核函数
在机器学习中常用的核函数,一般有这么几类,也就是LibSVM中自带的这几类:
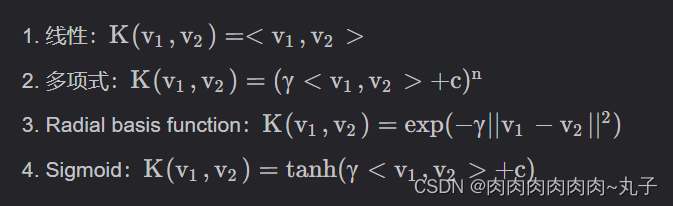
我举的例子是多项式核函数中γ=1, c = 0 n = 2 的情况。
3.核函数的性质
核函数只是满足某些必要条件的函数,其作用要与具体的算法结合才能显示出来。
我来简明说一下SVM中核技巧(kernel trick)的作用,一句话概括的话,就是降低计算的复杂度,甚至把不可能的计算变为可能。
核函数有如下一个性质:

4.核函数与SVM
求解SVM时,原始形式(这里我们假设已经对原始的输入做了变换,即输入模型的样本变成了ϕ ( x )

i = 1 , 2… N(N为样本个数)
这是个二次规划,因为未知量的个数是参数w的维度,而w的维度与样本的维度相等,即等于变换后ϕ ( x ) \phi(x)ϕ(x)的的维度,所以其求解复杂度与样本的维数正相关,这意味着,如果我们把原始样本从十维空间变换到一万维的空间,那么求解该问题的时间复杂度提升了1000倍或者更多,我们知道有些变换可以将样本换边到无穷维空间,那么这种变化之后直接是不可求解的。
上面的问题可以使用对偶 + 核技巧的组合来解决。
我们也知道,SVM原始形式的对偶问题是:

很明显,未知量α \alphaα的个数与样本的个数是相等的,那么这个对偶问题计算的时间复杂度是与训练样本的个数正相关的(这也是为啥样本个数太多的时候不推荐使用带核技巧的SVM的原因)。