标题
- 1 题目
- 2 实验原理
- 2.1 蒙特卡洛模拟的基本思想
- 2.2 电子散射的基本概念
- 3 代码
1 题目
扫描透射电镜(STEM)的基本原理是用极细的扫描电子束透射样品,透射电子直接被具有一定张角的接收器所接收,透射电流的强度直接反应了样品的质量厚度。
对于一定厚度的样品,采用蒙特卡洛方法模拟电子在样品中的散射过程,分析投射样品的电子的角度分布,计算散射角小于接收器张角的电子数目,电子透过率为 。
任务:扫描透射电子显微镜电子透过率的计算
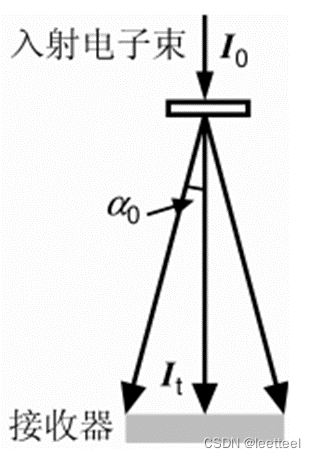
任务1:模拟电子在Al材料中的运动过程。
任务2:计算不同能量的入射电子穿透不同厚度后,一定接受角对应的电子透过率。
2 实验原理
2.1 蒙特卡洛模拟的基本思想
对求解问题本身就具有概率性和统计性的情况,例如中子在介质中传播,核衰变过程等,我们可以使用直接蒙特卡洛模拟方法。该方法是按照实际问题所遵循的概率规律统计规律,用电子计算机进行直接的抽样试验,然后计算其统计参数。直接蒙特卡洛模拟法最充分体现出蒙特卡洛方法无可比拟的特殊性和优越性,因为在物理学的各种各样问题中得到广泛的应用。该方法也就是通常所说的“计算机实验”。
2.2 电子散射的基本概念
一定能量的电子(大于数10eV)与材料原子发生相互作用所产生动量和能量变化的过程(俗称碰撞)。
电子散射可以分为两大类:弹性散射和非弹性散射,其区别在于散射过程中原电子的能量是否发生变化。
自由程:当一个电子在材料中运动时,会以一定的几率与材料原子发生散射。可以认为散射发生在一个点上,而在连续的两次散射之间,电子作自由(匀速直线运动)。其中电子在连续两次散射之间运动的路程为自由程。
3 代码
E0=300;
alpha=0.1;
alpha1=0.05;
I0 = 50000;
i = 0;
y = zeros(1,16);
y1 = zeros(1,16);
H = 0*10^-6:1*10^-6:15*10^-6;
for h=0*10^-6:1*10^-6:15*10^-6
i = i+1;
number=calc(E0,alpha,h,I0);
y(i)=number/I0;
number1=calc(E0,alpha1,h,I0);
y1(i)=number1/I0;
end
semilogy(H,y,'-r',Marker="square");
hold on;
semilogy(H,y1,'-g',Marker='o');
xlabel('材料厚度(m)')
ylabel('I/I0')
text(10*10^-6,0.45,'100mrad')
text(10*10^-6,0.2,'45mrad')
clc
clear
d=5*10^-6; %厚度设置为5微米
alpha=0.1;%角度
alpha1=0.045;
I0 = 20000;%总发射电子数
y_r = [];
y1_r = [];
for E0=100:20:500 %入射电子能量范围
number=calc(E0,alpha,d,I0);%100mrad
y=number/I0; %透过率
number1=calc(E0,alpha1,d,I0);%45mrad
y1=number1/I0; %计算不同张角下的透过率
y_r = [y_r,y];
y1_r = [y1_r,y1];
end
E0=100:20:500;
semilogy(E0,y_r,'-r',Marker="square");
hold on;
semilogy(E0,y1_r,'-g',Marker='o');
xlim([0 500])
xlabel('电子能量(keV)')
ylabel('I/I0')
text(250,0.6,'100mrad')
text(250,0.25,'50mrad')
function [It]=calc(E0,alpha,T,I0)
%E0电子入射能量,alpha角度,T厚度
keV = 1.6*10^-16;%能量,千电子伏,与E0相乘得到初始能量
eV = 1.6*10^-19;%电子电量
Z = 13;%原子序数
h = 6.626*10^-34;%普朗克常量
c = 3*10^8;%光速
a0 = 0.0529*10^-9;%波尔半径
m0 = 9.11*10^-31;%电子质量
%N = 7.5*10^28;%材料电子密度
N = 6*10^28;%单位体积靶原子个数
%T = 100*10^-6;%材料厚度(m)
phi0 = 0.117*Z^(1/3)/(E0)^0.5;
nuR = h/(2*m0*eV*(1+eV/(2*m0*c^2)))^0.5;
sigma = nuR^4*Z^2/(16*pi^3*a0^2*(phi0/2)^2*(1+(phi0/2)^2));
nu = 1/(N*sigma);%平均自由程
nu = nu+556*10^-9;%实际上应该是这个数量级
%I0 = 100;%总发射电子数
It = 0;%接收区内电子数
RAD = alpha;%接收角度
for i=1:1:I0%总运算次数(发射电子个数)
r0 = [0,0,0];%初始位置(前一时刻)
n0 = [0,0,1];%初始方向
r1 = [0,0,0];%后一时刻
n1 = [0,0,0];
rad = 0;
for j=1:1:10000%计算单个粒子,单次计算最多10000步
if r0(3)>T%材料厚度,大于厚度就算打穿,进入角度判定
if rad<=RAD
It = It+1;
end
break;
elseif r0(3)<0%小于0了,就视为反射出材料
break;
end
%初始方向计算两个角度
cos_k1=n0(3);
sin_k1 = sqrt(1-cos_k1^2);
if sin_k1==0
sin_kk1 = 0;
else
sin_kk1 = n0(2)/sin_k1;
end
cos_kk1 = sqrt(1-sin_kk1^2);
%散射角
r = rand(1);
cos_k = 1-(r*phi0^2)/2/(1+phi0^2/4-r);
sin_k = sqrt(1-cos_k^2);
%方位角
rr = rand(1);
kk = 2*pi*rr;
cos_kk=cos(kk);
sin_kk=sin(kk);
%单程s
rrr = rand(1);
s = -nu*log(rrr);
%新的运动方向
nn = [cos_k1*cos_kk1,-sin_kk1,sin_k1*cos_kk1;
cos_k1*sin_kk1,cos_kk1,sin_k1*sin_kk1;
-sin_k1,0,cos_k1];
n2 = [sin_k*cos_kk,sin_k*sin_kk,cos_k];
n1 = (nn*n2')';
n0 = n1;
%电子行进
r1 = r0+s*n1;
r0 = r1;
rad=(n1(1)^2+n1(2)^2)^0.5/(n1(1)^2+n1(2)^2+n1(3)^2)^0.5;%小角度近似,计算方向角度
end
end
end