​作者：小妮无语
专栏：一日一题

🚶‍♀️✌️道阻且长，不要放弃✌️🏃‍♀️

今天来更前几天做的，怕忘记了hh

并查集

​​​​

题目描述(集合合并)

一共有n个数，编号是1~n，最开始每个数各自在一个集合中。

现在要进行m个操作，操作共有两种：

“M a b”，将编号为a和b的两个数所在的集合合并，如果两个数已经在同一个集合中，则忽略这个操作；
“Q a b”，询问编号为a和b的两个数是否在同一个集合中；

输入格式
第一行输入整数n和m。

接下来m行，每行包含一个操作指令，指令为“M a b”或“Q a b”中的一种。

输出格式
对于每个询问指令”Q a b”，都要输出一个结果，如果a和b在同一集合内，则输出“Yes”，否则输出“No”。

每个结果占一行。

数据范围
1≤n,m≤105
输入样例：

4 5
M 1 2
M 3 4
Q 1 2
Q 1 3
Q 3 4

输出样例：

Yes
No
Yes

代码

#include<iostream>
using namespace std;
const int N=1e5+10;

int dis[N];
int n,m;

int find(int x)//查找根节点，根节点的特征就是父节点是自己
{
    while(x!=dis[x]) dis[x]=find(dis[x]);
    return dis[x];
    //这里实现了路径压缩的优化，每个节点的父节点都变成了根节点
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++) dis[i]=i;
    //把每个结点的父节点都先初始化成自己
    //但是到最后只有根节点的父节点是自己
    
    char a[2];//可以过滤空格
    int x,y;
    
    while(m--)
    {
        cin>>a;
        cin>>x>>y;
        if(a[0]=='M')//集合合并
        {
            dis[y]=find(x);
            //将其中一个集合本来的根节点的父节点指向另一个集合的根节点
        }
        else
        {
            if(find(x)!=find(y))
            //如果节点的根节点不同说明不在一个集合，以为根节点编号就是集合编号 
                puts("No");
            else
                puts("Yes");
        }
    }
    return 0;
}

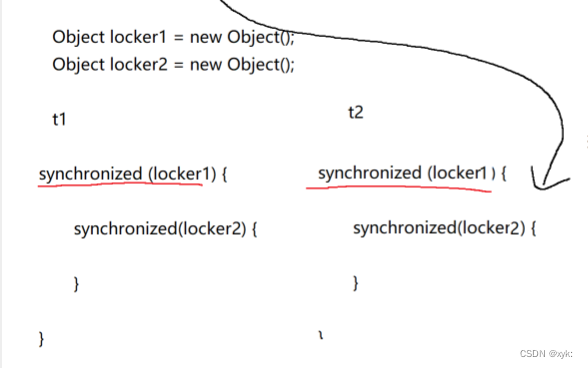
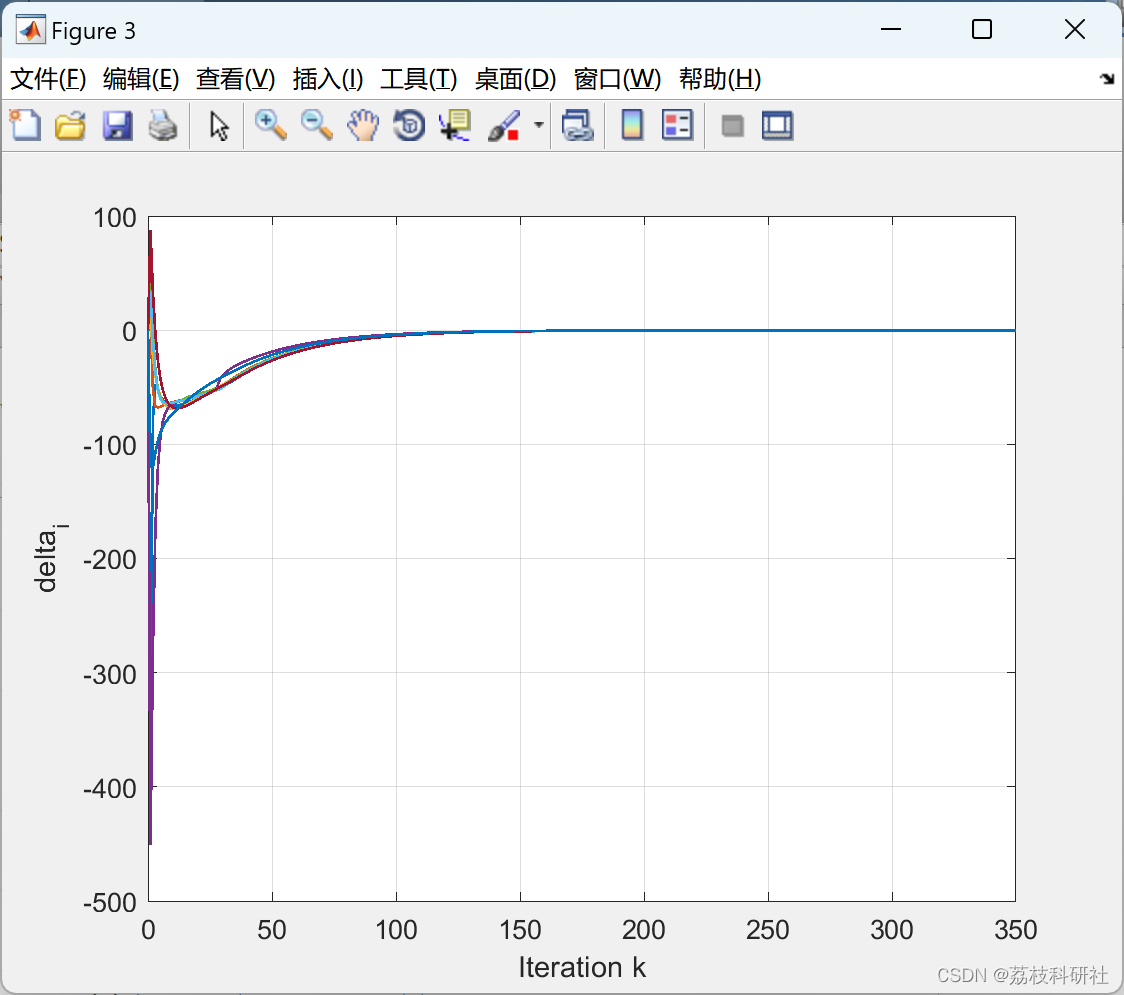
对路径压缩的解释

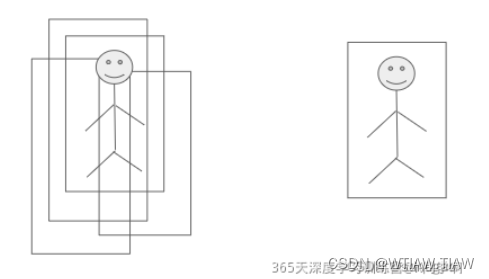
这里刚开始我不明白哪里优化了？不是路径压缩了吗？没看出来
其实在 find 函数里面是采用的递归，当你找到根节点以后，就会往上层弹出，然后dis[x]就会被更新为它前一层的dis[x]的值，dis[x]最终就是根节点的编号，所以所有的被递归过的节点的父节点都变成了根节点
缺点：不得不说它破坏了，本身树的结构
偷个图让大家看看，我感觉这个图非常(๑•̀ㅂ•́)و✧

二叉树遍历

题目描述

编写一个程序，读入用户输入的一串先序遍历字符串，根据此字符串建立一个二叉树（以指针方式存储）。

例如如下的先序遍历字符串： abc##de#g##f### 其中 # 表示的是空格，空格字符代表空树。

建立起此二叉树以后，再对二叉树进行中序遍历，输出遍历结果。

输入格式
共一行，包含一个字符串，表示先序遍历字符串。

输出格式
共一行，输出将输入字符串建立二叉树后中序遍历的序列，字符之间用空格隔开。

注意，输出中不用包含 #。

数据范围
输入字符串长度不超过 100，且只包含小写字母和 #。

输入样例：

abc##de#g##f###

输出样例：

c b e g d f a

代码

#include<iostream>
using namespace std;
string s;
int idx;

void dfs()
{
    if(s[idx]=='#')
    {
        idx++;
        return;
    }
    char a=s[idx++];//记录本层的根节点
    
    dfs();//遍历左子树
    cout<<a<<' ';//被弹回来了，就输出本层的根节点
    dfs();//然后看看右子树，如果被弹回来，就直接从上次的左子树遍历的dfs(),弹出来了
    //到本层的上一层，然后输出本层上层的根节点,然后继续遍历本层上层的右子树
}
int main()
{
    cin>>s;
    dfs();
    return 0;
}

这个超有趣，其实你细品，cout 放哪里，你就对于什么排序，cout 放在左子树遍历前，它就是先序遍历，放中，就是中序遍历，放后就是后序，它对应根的输出位置

         == 欢迎来到一日一题的小菜鸟频道，睡不着就看看吧！==

                        ==  跟着小张刷题吧！==