1.什么是伯努利分布？

伯努利分布是一种二元随机变量的概率分布，其中一个结果的概率为p，另一个结果的概率为1-p。伯努利分布通常用于模拟二项分布，其中n个独立的伯努利试验被执行，每个试验有两个可能的结果（成功或失败），且每个试验成功的概率是p。当n=1时，伯努利分布退化成了一个简单的二元随机变量的概率分布。

我们可以在python中很容易的实现它，代码如下：

import numpy as np
import matplotlib.pyplot as plt

p = 0.7  # 成功的概率
size = 1000  # 样本数量

# 生成伯努利分布样本
samples = np.random.binomial(n=1, p=p, size=size)

# 统计样本中 0 和 1 的数量
counts = np.bincount(samples)

# 绘制伯努利分布图
plt.bar(x=[0, 1], height=counts, width=0.5, align='center')

# 设置图表标题和轴标签
plt.title("Bernoulli Distribution")
plt.xlabel("Sample Values")
plt.ylabel("Counts")

# 设置 x 轴的刻度标签
plt.xticks([0, 1], ["0", "1"])

# 显示图表
plt.show()

显示的图表效果如下

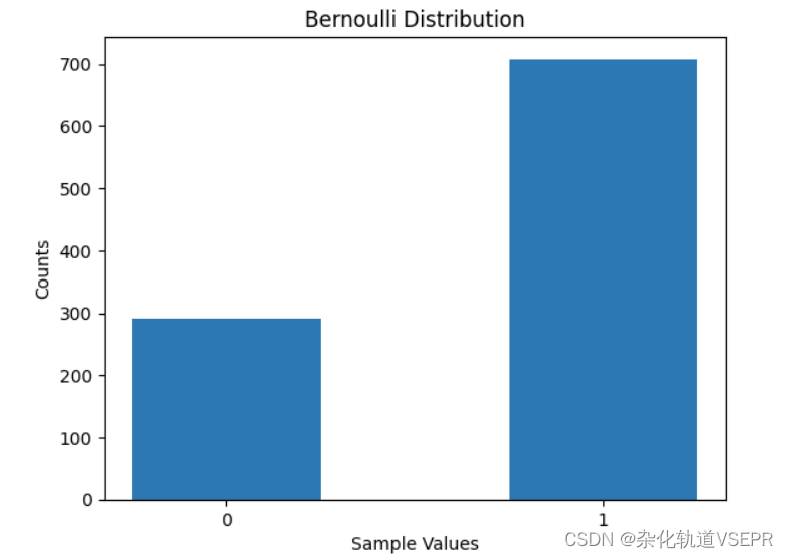
如果需要大量实验来复盘结果，修改一下size的值就可以了

2.什么是二项式分布？

二项分布是一种离散概率分布，描述了在n次独立的伯努利试验中成功k次的概率，其中每次试验成功的概率为p。如果每次试验成功的概率为p，失败的概率为1-p，则二项分布的概率质量函数为：

$P(X=k)=\left(\genfrac{}{}{0ex}{}{n}{k}\right)p^k(1-p{)}^{n-k}$

其中，$\left(\genfrac{}{}{0ex}{}{n}{k}\right)$ 表示组合数，表示从n个元素中选择k个元素的组合数量。

在Python中，可以使用 SciPy 库中的 binom 函数来计算二项分布的概率密度和分布函数，以及生成随机样本。下面是一个使用 binom 函数计算二项分布概率密度和绘制概率质量函数图的示例代码：

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom

n = 10  # 试验次数
p = 0.5  # 成功的概率

# 计算二项分布的概率密度
k = np.arange(0, n+1)  # 成功次数
pdf = binom.pmf(k, n, p)  # 概率密度函数

# 绘制概率质量函数图
plt.stem(k, pdf, use_line_collection=True)

# 设置图表标题和轴标签
plt.title("Binomial Distribution (n=10, p=0.5)")
plt.xlabel("Number of Successes")
plt.ylabel("Probability Density")

# 显示图表
plt.show()

显示效果如下：

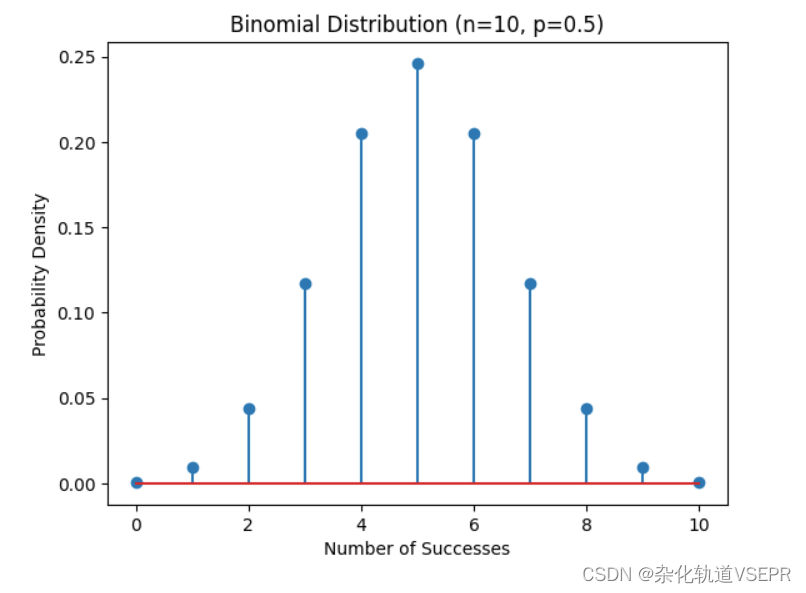
3.泊松分布是指在一定时间内，某一时间发生的次数在概率图上面的分布。泊松分布在日常事件里的特点是可以预估事件发生的总次数，但是不能估计事件发生的时间节点，它的python实现如下：

#Q 写一段泊松分布的代码

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson

mu = 10  # 平均值

# 计算泊松分布的概率质量
k = np.arange(0, 30)  # 成功次数
pmf = poisson.pmf(k, mu)  # 概率质量函数

# 绘制概率质量函数图
plt.stem(k, pmf, use_line_collection=True)

# 设置图表标题和轴标签
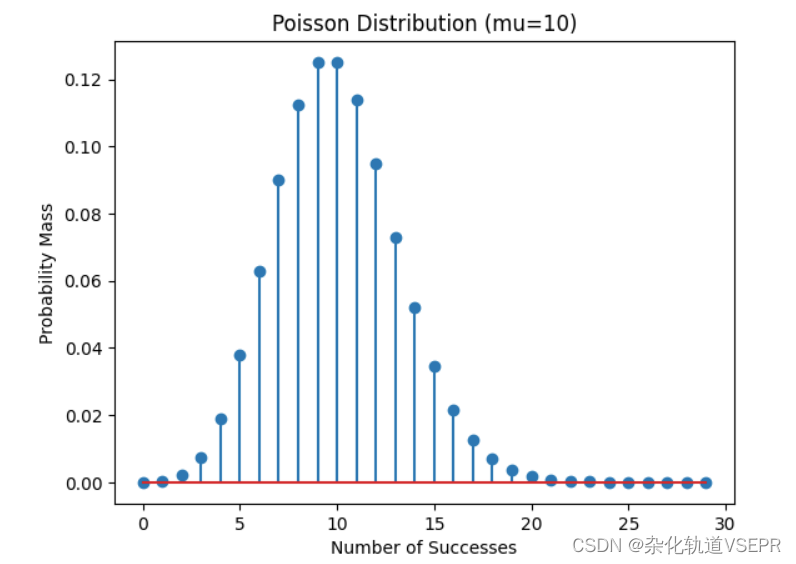
plt.title("Poisson Distribution (mu=10)")
plt.xlabel("Number of Successes")
plt.ylabel("Probability Mass")

# 显示图表
plt.show()

它的图像如下：