树上差分一般有两种类型的题目,一种是对边进行差分,另一种就是对点进行差分。
对应的操作也有两种,对边进行差分的对应操作就是给定一对节点(u,v),让我们把u到v之间路径上的边权都加val,对点进行差分的对应操作就是给定一对节点(u,v),让我们把u到v之间路径上所经过的点的点权都加val,这两种操作是类似的,但又不完全一样,下面分别讲解一下这两种问题应该如何处理。
首先先来说一下将u到v之间路径上的边权都加val应该怎么处理。
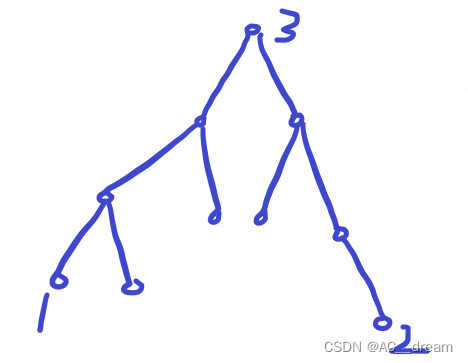
以这个图为例子,我们假如要将1到2之间路径上的边权都加val,那么我们可以将边权唯一地对应到点权上,什么意思呢?因为对于树上的任意一个节点都有其对应的深度,那么对于同一条边所连接的两个节点的深度又是不同的,所以我们可以定义一条边权为以其连接的两个节点中的深度较大的节点为根的子树中所有节点的点权和,这样我们就可以唯一地确定每条边的边权。
那么我们要是想要把1到2之间路径上的边权都加val,我们可以把1号节点和2号节点的点权都加上val,这样凡是子树中包含节点1或2的节点的权值都会对应地加上val,我们只需要回溯的过程中更新一下以每个节点为根的子树中的节点点权之和即可,但是我们可以发现1和2的最近公共祖先3点权加了2*val,但是3号节点的点权是3号节点与其父节点之间的边权,不属于1和2之间路径的边权,所以我们应该将1和2的最近公共祖先点权减少2*val。这样就完成了更新。
还有一种常见操作就是点差分,还是以上面那个图为例,我们现在要将1到2的路径上的所有节点的权值加val,那么我们定义点权和上面边差分类似,定义一个节点的点权为以节点为根的子树中所有节点的点权和,那么我们现在要想将1到2的路径上的所有节点的权值加val,我们依旧可以先将节点1、2的点权+val,然后同理我们可以发现1和2的公共祖先3的点权相当于+2*val,但由于3号节点也属于1到2的路径上的节点之一,所以我们只需要减去val即可,但是这还不算结束,因为3号节点的父亲节点不属于1到2的路径上的节点之一,但是因为3号节点的点权加了val,而3号节点又是3号节点的子树中的节点,所以我们还应该把其父亲节点的权值减去val,这样才算是操作结束。
下面给出一道对应习题及其代码:
题目连接:P3128 [USACO15DEC]Max Flow P - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

样例输入:
5 10
3 4
1 5
4 2
5 4
5 4
5 4
3 5
4 3
4 3
1 3
3 5
5 4
1 5
3 4样例输出:
9代码:
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
const int N=2e5+10;
int h[N],e[N],ne[N],idx;
int f[N][25],d[N],s[N];
void add(int x,int y)
{
e[idx]=y;
ne[idx]=h[x];
h[x]=idx++;
}
void dfs(int x,int fa,int dd)
{
d[x]=dd;
f[x][0]=fa;
for(int i=1;i<=20;i++)
f[x][i]=f[f[x][i-1]][i-1];
for(int i=h[x];i!=-1;i=ne[i])
{
int j=e[i];
if(j==fa) continue;
dfs(j,x,dd+1);
}
}
int lca(int x,int y)
{
if(d[x]<d[y]) swap(x,y);
for(int i=20;i>=0;i--)
if(d[f[x][i]]>=d[y]) x=f[x][i];
if(x==y) return x;
for(int i=20;i>=0;i--)
if(f[x][i]!=f[y][i])
{
x=f[x][i];
y=f[y][i];
}
return f[x][0];
}
void update(int x,int fa,int &ans)
{
for(int i=h[x];i!=-1;i=ne[i])
{
int j=e[i];
if(j==fa) continue;
update(j,x,ans);
s[x]+=s[j];
}
ans=max(ans,s[x]);
}
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
h[i]=-1;
for(int i=1;i<n;i++)
{
int x,y;
scanf("%d%d",&x,&y);
add(x,y);add(y,x);
}
dfs(1,0,1);
for(int i=1;i<=m;i++)
{
int x,y;
scanf("%d%d",&x,&y);
int t=lca(x,y);
s[x]++;s[y]++;
s[t]--;
s[f[t][0]]--;
}
int ans=0;
update(1,0,ans);
printf("%d",ans);
return 0;
}