目录

1、二叉树的( )遍历相当于广度优先遍历，( )遍历相当于深度优先遍历

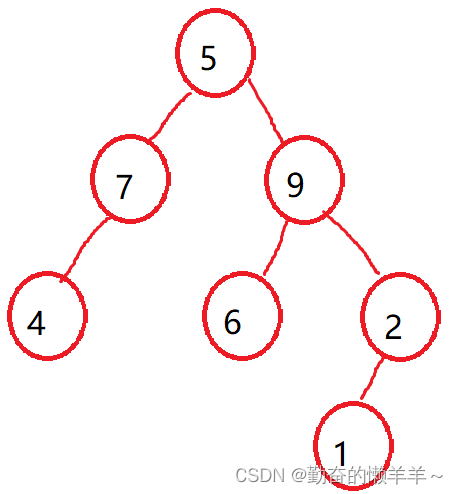
2、已知某二叉树的前序遍历序列为5 7 4 9 6 2 1，中序遍历序列为4 7 5 6 9 1 2，则其后序遍历序列为（ ）

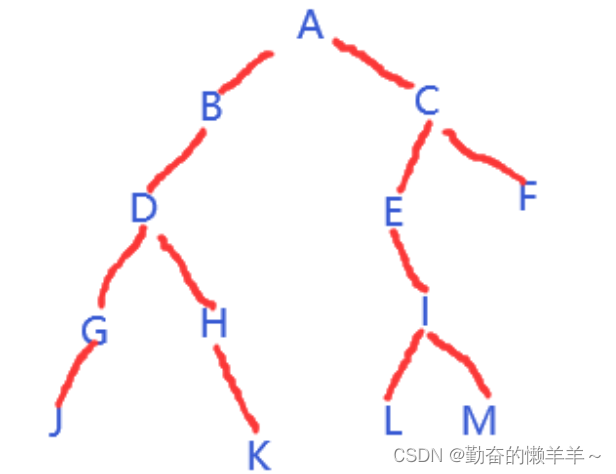
3、已知某二叉树的中序遍历序列为JGDHKBAELIMCF，后序遍历序列为JGKHDBLMIEFCA，则其前序遍历序列为（ ）

4、如果一颗二叉树的前序遍历的结果是ABCD，则满足条件的不同的二叉树有（ ）种。

---

1、二叉树的( )遍历相当于广度优先遍历，( )遍历相当于深度优先遍历

A.前序 中序

B.中序 前序

C.层序 后序

D.层序 前序

答案：C

2、已知某二叉树的前序遍历序列为5 7 4 9 6 2 1，中序遍历序列为4 7 5 6 9 1 2，则其后序遍历序列为（ ）

A.4 2 5 7 6 9 1

B.4 2 7 5 6 9 1

C.4 7 6 1 2 9 5

D.4 7 2 9 5 6 1

答案：C

解析：首先，根据前序序列可知，根节点为5，7只能是5的左结点或右结点，

又因为在中序遍历中，根节点左边的一定是左子树，根节点右边的一定是右子树，

7在5左边，所以7是5的左节点。

再把7看成根，根据中序序列，它的左子树只有结点4，

再把4看成根，根据中序序列，4的左边已经没有结点了，

因时，5的左子树就排好了。

此时，根据前序序列，9一定是5的右结点，把9看成根，

根据中序序列，9的左边只有6了，所以6一定是9的左子树，

再根据前序序列，2是9的右子树，把2看成根

根据中序序列，2的左边还剩1，所以1是2的左子树。

此时，5的右子树也排好了。

简洁版：根为： 5

5的左子树：4 7   5的右子树： 6 9  1  2

5的左子树的根为: 7  5的右子树的根为：9

7的左子树: 4 7的右：空  9的左子树：6  9的右子树：2

3、已知某二叉树的中序遍历序列为JGDHKBAELIMCF，后序遍历序列为JGKHDBLMIEFCA，则其前序遍历序列为（ ）

A.ABDGHJKCEFILM

B.ABDGJHKCEILMF

C.ABDHKGJCEILMF

D.ABDGJHKCEIMLF

答案：B

解析：由后序遍历确定子树的根，后序遍历从后向前看，最后一个元素为根，和前序遍历刚好相反，从后向前看后序遍历，应该是根，右，左，根据中序遍历确定子树的左右区间

故：根为: A

A的左子树：JGDHKB       A的右子树：ELIMCF

A的左子树的根：B        A的右子树的根：C

B的左子树：JGDHK  B的右子树：空  C的左子树：ELIM C的右子树：F

B的左子树的根：D         C的左子树根：E

D的左子树的根：G D的右子树的根：H  E的右子树的根:I

故树的结构为：

4、如果一颗二叉树的前序遍历的结果是ABCD，则满足条件的不同的二叉树有（ ）种。

首先，树的高度一定为3-4层。

三层：

A(B(C,D),()), A((),B(C,D)), A(B(C,()),D), A(B((),C),D),

A(B,C(D,())), A(B,C((),D))

四层：

如果为四层，就是单边树，每一层只有一个节点，除过根节点，其他节点都有两种选择，在上层节点的左边还是右边，所以2*2*2共8种

答案：总共为14种。