c++算法初级8——递推

递推

递推思想：

根据已有的东西一点点地推出未知的东西。

使用递推解题三步骤：

• 数学建模
• 找出递推式和初始条件
• 写出代码。

张爽的青蛙（斐波那契）问题：地上有n个石头从左到右排成一排，张爽同学养的青蛙要从第一个石头跳到最后一个石头上，每次可以选择向右跳一格或者跳两格，问总共有多少种不同的走法？

递推表达式：设跳到第i格有$f(i)$个跳法，则$f(i)=f(i-1)+f(i-2)$
初始条件：f[1] = f[2] = 1。因为从1走到1只有一种方案（呆在原地不动），从1走到2也只有一种方案（走一格）；
代码：

# include "bits/stdc++.h"
using namespace std;
const int MOD = 998244353; // 答案对998244353取模。
int k, f[1000010];

int main()
{
    cin >> k;
    f[1] = 1;
    f[2] = 1;
    for (int i = 3; i <= k; i++)
    {
        f[i] = (f[i - 1] + f[i - 2]) % MOD;
    }
    cout << f[k] << endl;
    return 0;
}

卡特兰数问题：由n对括号组成的括号序列，有多少种是合法的括号序列？答案对998244353取模。

什么是合法的括号序列？其定义如下：

空序列是合法的括号序列
如果A是合法的括号序列，那么(A)是合法的括号序列
如果A和B是合法的括号序列，那么AB也是合法的括号序列

简单通俗地讲，合法的括号序列就是：任何一个左括号都必须有与之对应的右括号，任何一个右括号都必须有与之对应的左括号。

比如：

()(()(()))是合法的括号序列
)(不是合法的括号序列，因为第一个右括号没有与之对应的左括号
(()))不是合法的括号序列，因为最后一个右括号没有与之对应的左括号

类似的，如果我们想用递推解决问题，我们就要找到递推式。首先开一个数组int f[n]，用f[i]来表示i对括号能够组成多少种合法的括号序列。那么，怎么根据f[0], f[1], f[2], …, f[k-1]的值推出f[k]的值呢？

我们继续使用分类讨论的思想：由于合法括号序列的最后一个字符一定是右括号，不妨假设最终的括号序列长成这个样子：A(B)。其中，A和B都是合法括号序列（注意A和B可以是空序列）。

我们把最终的序列分成k种：

A由0对括号组成，B由k-1对括号组成，这样的序列有f[0] * f[k-1]种
A由1对括号组成，B由k-2对括号组成，这样的序列有f[1] * f[k-2]种
A由2对括号组成，B由k-3对括号组成，这样的序列有f[2] * f[k-3]种
……
A由m对括号组成，B由k-1-m对括号组成，这样的序列有f[m] * f[k-1-m]种
……
A由k-1对括号组成，B由0对括号组成，这样的序列有f[k-1] * f[0]种

由此，就得到了递推式

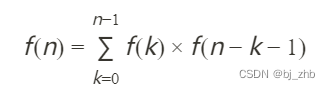
初始条件：
f(0)=1，，因为0对括号只能组成一种括号序列（空序列）
代码

# include"bits/stdc++.h"
using namespace std;
const int MOD = 998244353;
int n, f[100010];

int main() {
    cin >> n;
    f[0] = 1;
    for (int i = 1; i <= n; i++) {
        for (int j = 0; j < i; j++) {
            f[i] = (f[i] + 1ll * f[j] * f[i - j - 1]%MOD) % MOD;
        }
    }
    cout << f[n] << endl;
    return 0;
}

时间复杂度$O(n^2)$

递推思想的运用

错位排序

错位排列

有n个信封和n个信件，第i个信件属于第i个信封，我们想知道，有多少种不同的方法，使得没有任何一个信件被装入正确的信封中？答案对998244353取模。
下图中，2号信件装入了2号信封中，因此方案不合法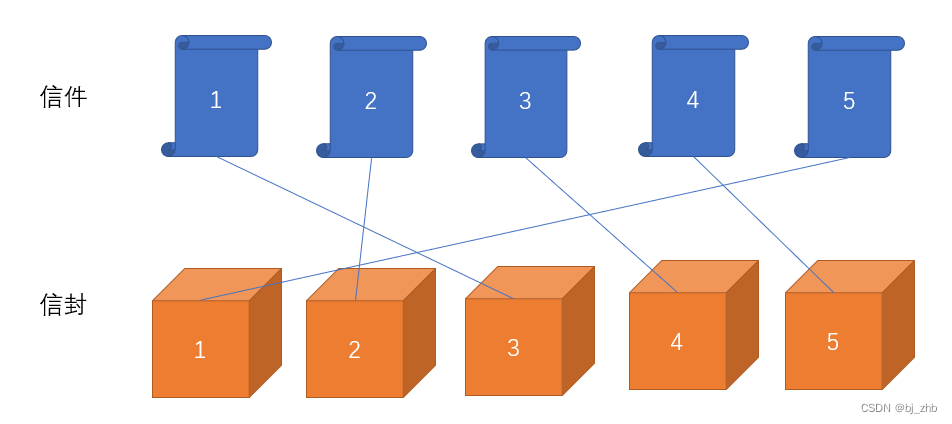
而下图，就满足“任何一个信件都没有被装入正确的信封中”，因此是合法方案：

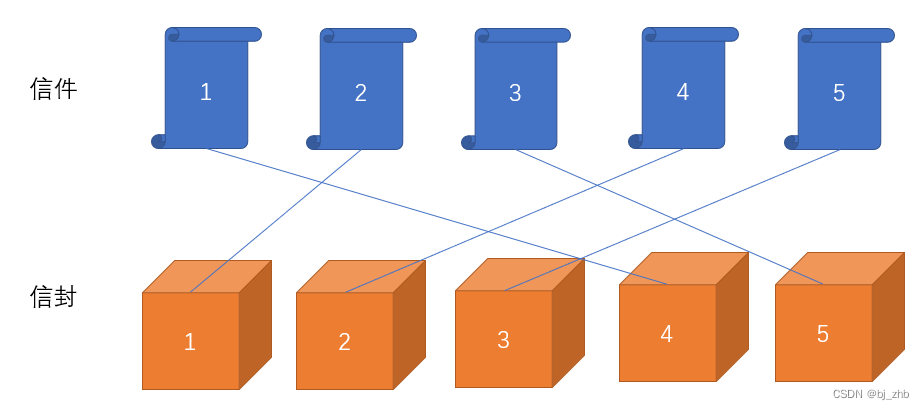
我们开一个数组int f[n];，其中f[i]表示当信封和信件数量为i的时候，总方案数是多少。接下来，我们应该如何寻找递推式呢？

f(1)=0, f(2)=1是初始条件
考虑1号信件，它不能被装入1号信封，不妨假设它被装入了x号信封。这里为了方便，我们假设x = 3。
那么x号信件可以装入哪个信封呢？这里又存在两种情况。

第一种情况：x号信件装入了1号信封：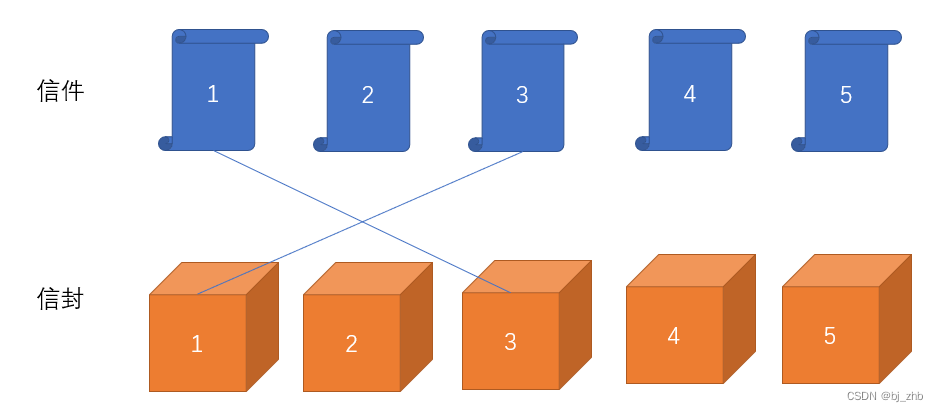
在这种情况下，我们可以去掉1号和x号，就变成了完全独立的子问题：n-2个信件和信封的错位排列问题。

第二种情况：x号信件没有装入1号信封。这个时候，如果我们去掉1号信件和x号信封，情况就会变成下图：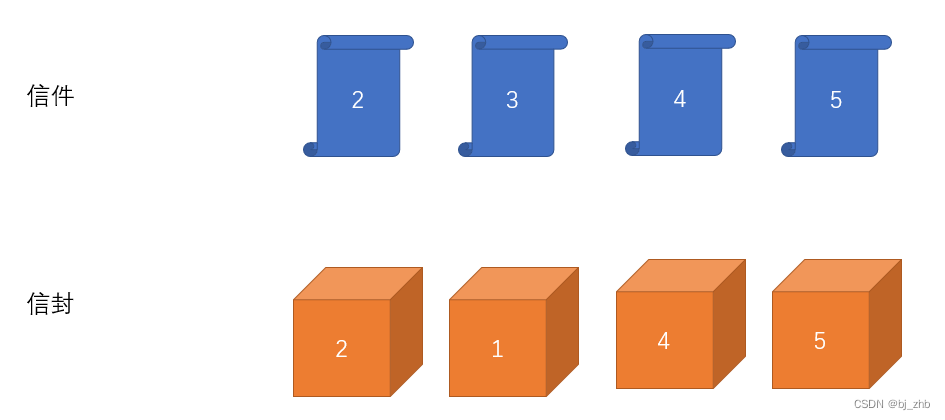
2号、4号、5号信件不能装入对应的信封中，而x号信件不能装入1号信封中，这其实也是一个大小为n-1的错位排列问题。
因此，当1号信件装入x号信封的时候，总共会有两种情况：

• x号信件装入1号信封，有f[n-2]种方案
• x号信件不装入1号信封，有f[n-1]种方案

而x的选择有n-1种（除了1都可以），因此我们得到了递推式f[n] = (n-1)(f[n-1] + f[n-2])。

代码

/*有n个信封和n个信件，第i个信件属于第i个信封，我们想知道，有多少种不同的方法，
使得没有任何一个信件被装入正确的信封中？答案对998244353取模。*/
# include<bits/stdc++.h>
using namespace std;

const int mod = 998244353;
const int maxn = 100000 + 10;
//递推算法f(n) = (n-1) * (f(n-1) + f(n-2))
int main()
{
    int n;
    cin >> n;
    int f1 = 0, f2 = 1;
    int ans = 1;
    for(int i = 3; i <= n; i++)
    {
        ans = (1LL * (i - 1) * (f1 + f2) ) % mod;
        f1 = f2;
        f2 = ans;
    }
    cout << ans << endl;
}

杨辉三角（二维递推）

事实上，我们也会经常遇到不止一维的递推，比如我们接下来要介绍的杨辉三角问题。

比如，当k=4时，你需要输出如下矩阵：

1 0 0 0 0
1 1 0 0 0
1 2 1 0 0
1 3 3 1 0
1 4 6 4 1
其中第4行第2列的数字为6（注意行和列从0开始标号），表示从4个不同的物品中选2个有6种方法。
假设这4个物品分别叫A、B、C、D，那么这6种方法分别是：

AB
AC
AD
BC
BD
CD

类似的，我们开一个二维数组int f[k][k];，其中f[i][j]表示从i个物品中选j个的方案数，接下来，我们要做的就是寻找递推式。

怎么尝试寻找递推式呢？分类讨论吗？对的！我们继续使用分类讨论来寻找递推式。绝大多数简单的递推问题都可以用分类讨论的方法找到一个合理的递推式。

假设我们现在要求的值是f[i][j]，即，从i个物品中选j个的方案数，我们不妨把i个物品从1到i标上号。
现在考虑1号物品，我们尝试对1号物品进行分类讨论。怎么分类呢？无非就是两类：选1号物品，还是不选1号物品。

选1号物品：由于1号物品是一定要选进来的，因此我们还剩i-1个物品，我们要从中选出j-1个物品，方案数是f[i-1][j-1]。
不选1号物品：我们还剩i-1个物品，但是1号一定不选，因此我们还要从剩下的i-1个物品中选出j个物品，方案数是f[i-1][j]。
结束了吗？其实这样就结束了。因为我们已经不重复不遗漏地考虑到了所有可能出现的情况。

所以我们就得到了递推式：f[i][j] = f[i-1][j-1] + f[i-1][j]。

边界条件：
接下来，我们发现样例矩阵的第一列和对角线全都是1，这也是容易推理出的：第一列的所有元素都是f[x][0]，从x个物品中选取0个物品，显然只有一种方案：什么都不选；而对角线的所有元素都是f[x][x]，从x个物品中选出x个物品，也只有一种方案：全部都选上。

除此之外还有其他的边界条件吗？

没有了。

因为我们的递推式f[i][j] = f[i-1][j-1] + f[i-1][j]告诉我们，如果我们想要计算任何一个数字f[i][j]，只需要知道它“上面”的数字f[i-1][j]和“左上方”的数字f[i-1][j-1]即可。观察矩阵，我们发现，对于任何一个数字，我们都可以用已知的初始条件推出，因此我们不需要更多的边界条件了。

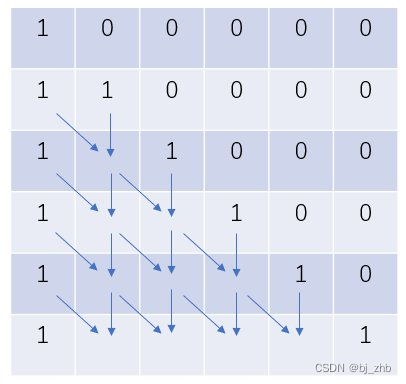
除此之外还有什么需要注意的么？有的！我们还需要特别注意递推的顺序！二维递推不同于一维递推，二维的数据可能存在莫名其妙的依赖关系，因此我们在写二维递推的时候，需要特别注意二维递推的顺序。

比如杨辉三角，我们可以从递推式和上图看出，f[i]这一行的值全部由f[i-1]这一行的值推出，因此我们只需要按照行数从小到大的顺序递推即可。而其他形式的二维递推可能就需要用其他顺序进行循环，比如下面这种递推形式。

搞定了递推式、初始条件、递推顺序之后，我们的代码就呼之欲出了。

同时，递推出单个元素的复杂度是O(1)，整个表格一共有O(n²)个元素，因此该算法的总时间复杂度是O(n²)。

// 杨辉三角递推
# include <bits/stdc++.h>
using namespace std;

int main()
{
    int n;
    cin >> n;
    vector<vector<int>> dp(n + 1, vector<int>(n + 1, 0));
    
    //dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
    //初始条件dp[i][0]=1,dp[i][i]=1，设置初始条件
    for(int i = 0; i <= n; i++)
    {
        dp[i][0] = 1;
        dp[i][i] = 1;
    }
    //递推
    for(int i = 2; i <= n; i++)
    {
        for(int j = 1; j <= i; j++)
        {
            dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
        }
    }
    //输出
    for(int i = 0; i <= n; i++)
    {
        for(int j = 0; j <= n; j++)
        {
            cout << dp[i][j] << " ";
        }
        cout << endl;
    }
}