一、概述

k-近邻算法（k-Nearest Neighbour algorithm），又称为KNN算法，是数据挖掘技术中原理最简单的算法。

KNN的工作原理：给定一个已知标签类别的训练数据集，输入没有标签的新数据后，在训练数据集中找到与新数据最邻近的k个实例，如果这k个实例的多数属于某个类别，那么新数据就属于这个类别。可以简单理解为：由那些离X最近的k个点来投票决定X归为哪一类。

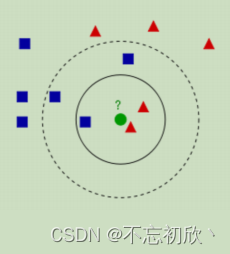
在这里插入图片描述
上图有红色三角和蓝色方块两种类别，我们现在需要判断绿色圆点属于哪种类别，我们会发现：
当k=3时，绿色圆点属于红色三角这种类别；
当k=5时，绿色圆点属于蓝色方块这种类别。

二、代码实现

# 使用sklearn中的knn算法接口实现
from sklearn.neighbors import KNeighborsClassifier 

clf = KNeighborsClassifier(n_neighbors=k)          #实例化
clf = clf.fit(X_train,y_train)                     #用训练集数据训练模型
result = clf.score(X_test,y_test)                  #导入测试集，从接口中调用需要的信息

三、K值的选择

K值的选择对KNN算法效果影响比较大，如果K太小，则最近邻分类器容易受到由于训练数据中的噪声而产生的过分拟合的影响；相反，当K值更大的时候，错误率会更高。这也很好理解，比如说你一共就35个样本，当你K增大到30的时候，KNN基本上就没意义了。一般我们使用学习曲线来判断K的取值，以下以sklearn中自带的手写体数据为例：

from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
#探索数据集
data = load_digits()
X = data.data
y = data.target
Xtrain,Xtest,Ytrain,Ytest = train_test_split(X,y              #特征和标签
                                           ,test_size=0.2    #测试集所占的比例
                                           ,random_state=1)
# 绘制学习曲线
score = [] #用来存放模型预测结果
krange = range(1,20)

for i in krange:
   clf = KNeighborsClassifier(n_neighbors=i)
   clf = clf.fit(Xtrain,Ytrain)
   score.append(clf.score(Xtest,Ytest))
print(score)
bestK = krange[score.index(max(score))]
print(bestK)
print(max(score))

plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']

plt.figure(figsize=(6,4),dpi=80)  #dpi是像素值
plt.plot(krange,score)

plt.title('K值学习曲线',fontsize=15)
plt.xlabel('K值',fontsize=12)
plt.ylabel('预测准确率',fontsize=12)
plt.xticks(krange[::3])  # x轴刻度
plt.show()

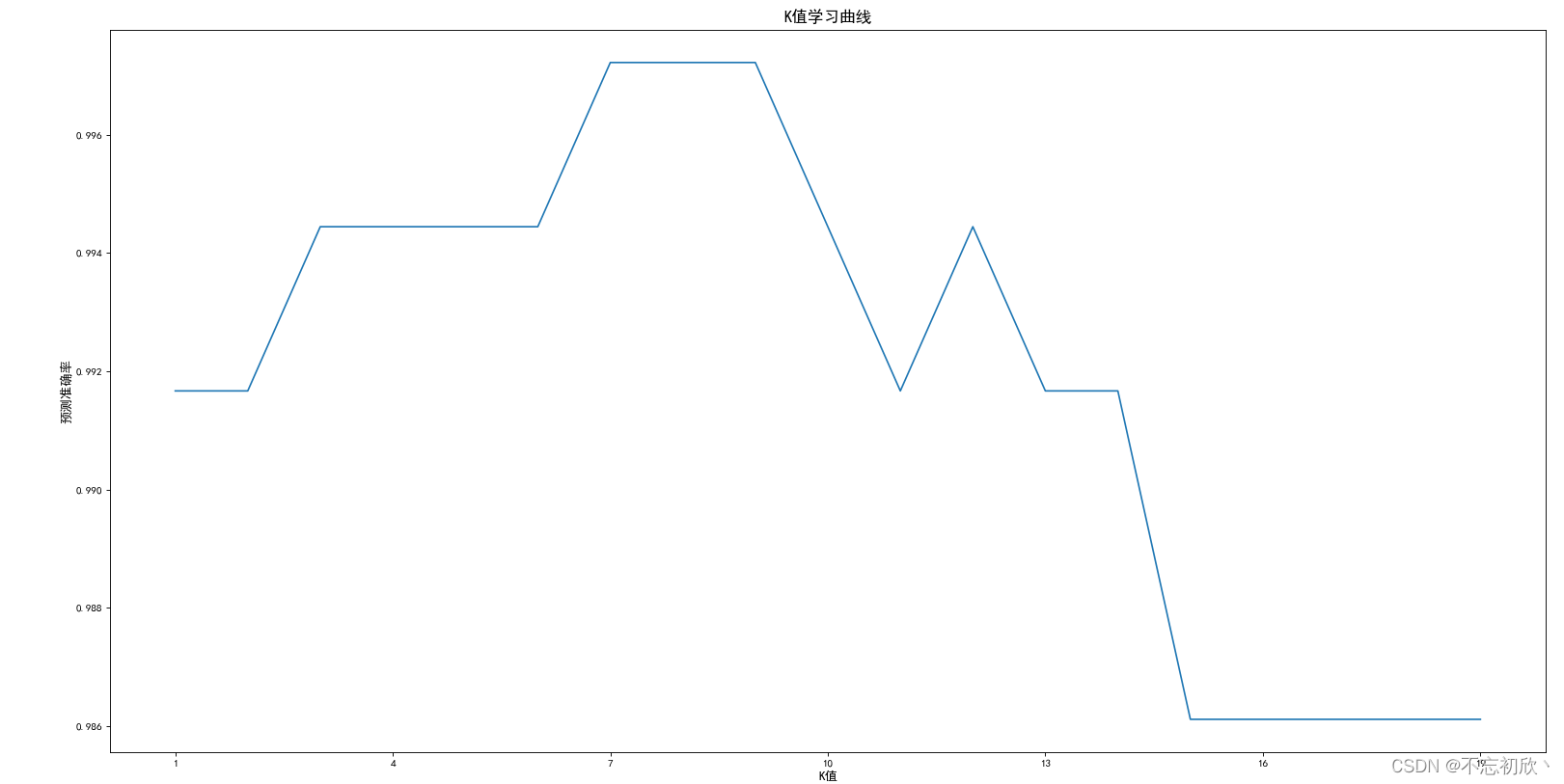
在这里插入图片描述
从学习曲线可以看出，当K=7时，得分最高为0.9972222222222222

四、距离计算

KNN属于距离类模型，原因在于它的样本之间的远近是靠数据距离来衡量的。欧几里得距离、曼哈顿距离、切比雪夫距离、闵可夫斯基距离等都是很常见的距离衡量方法。KNN中默认使用的是欧氏距离（也就是欧几里得距离）。

数据集中有的特征数值很大，有的特征数值很小，量纲不一致，在使用欧式距离计算的时候，距离容易受到量纲大的数据的影响，比如人的身高和体重，身高178cm，体重60Kg，因此对数据归一化来统一量纲，常用的数据归一化的处理方法有很多种，比如0-1标准化、最大最小归一化、Z-score标准化、Sigmoid压缩法等等

五、总结

1. K-近邻算法

算法功能	分类、回归
算法类型	有监督学习 - 惰性学习，距离类模型
数据输入	包含数据标签y，且特征空间中至少包含k个训练样本（k>=1) 特征空间中各个特征的量纲需统一，若不统一则需要进行归一化处理自定义的超参数k (k>=1)
模型输出	在KNN分类中，输出是标签中的某个类别在KNN回归中，输出是对象的属性值，该值是距离输入的数据最近的k个训练样本标签的平均值