LeetCode算法小抄-- 图的遍历
- 图
- 基本概念
- 遍历
- 广度优先算法(BFS)
- 框架
- [111. 二叉树的最小深度](https://leetcode.cn/problems/minimum-depth-of-binary-tree/)
- [752. 打开转盘锁](https://leetcode.cn/problems/open-the-lock/)
- [773. 滑动谜题](https://leetcode.cn/problems/sliding-puzzle/)
- 双向BFS
- 深度优先算法(DFS)
- [797. 所有可能的路径](https://leetcode.cn/problems/all-paths-from-source-to-target/)
⚠申明: 未经许可,禁止以任何形式转载,若要引用,请标注链接地址。 全文共计10038字,阅读大概需要3分钟
🌈更多学习内容, 欢迎👏关注👀【文末】我的个人微信公众号:不懂开发的程序猿
个人网站:https://jerry-jy.co/
图
基本概念
一幅图是由节点和边构成的,逻辑结构如下
/* 图节点的逻辑结构 */
class Vertex {
int id;
Vertex[] neighbors;
}
对比多叉树
/* 基本的 N 叉树节点 */
class TreeNode {
int val;
TreeNode[] children;
}
图的本质就是多叉树
用邻接表和邻接矩阵的存储方式如下
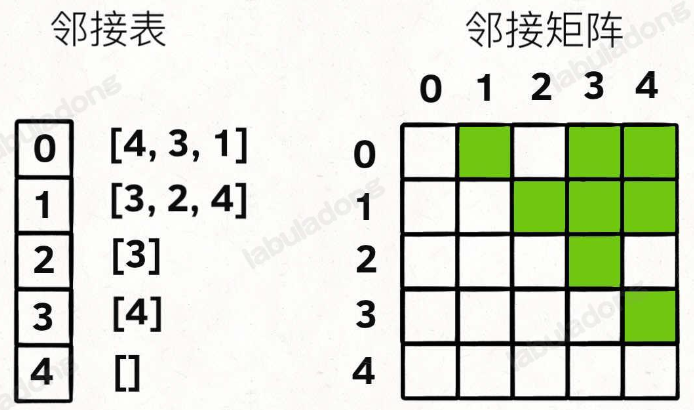
邻接表很直观,我把每个节点 x 的邻居都存到一个列表里,然后把 x 和这个列表关联起来,这样就可以通过一个节点 x 找到它的所有相邻节点。
邻接矩阵则是一个二维布尔数组,我们权且称为 matrix,如果节点 x 和 y 是相连的,那么就把 matrix[x][y] 设为 true(上图中绿色的方格代表 true)。如果想找节点 x 的邻居,去扫一圈 matrix[x][..] 就行了。
// 邻接表
// graph[x] 存储 x 的所有邻居节点
List<Integer>[] graph;
// 邻接矩阵
// matrix[x][y] 记录 x 是否有一条指向 y 的边
boolean[][] matrix;
对于邻接表,好处是占用的空间少。但是,邻接表无法快速判断两个节点是否相邻。各有优劣
度(degree)
在无向图中,「度」就是每个节点相连的边的条数。
由于有向图的边有方向,所以有向图中每个节点「度」被细分为入度(indegree)和出度(outdegree)
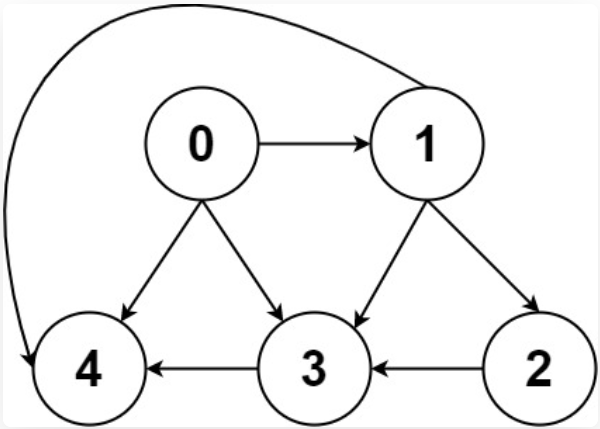
有向无权图
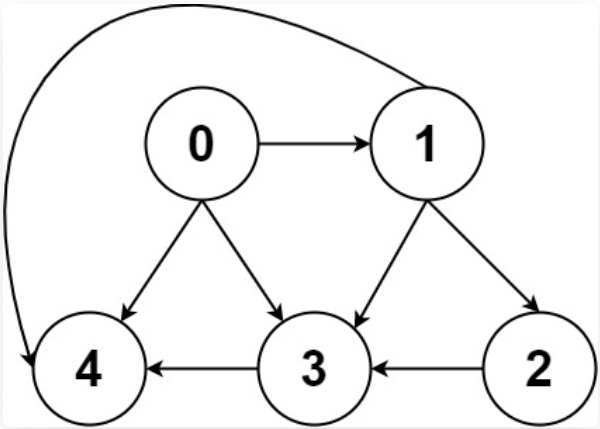
其中节点 3 的入度为 3(有三条边指向它),出度为 1(它有 1 条边指向别的节点)
有向加权图
如果是邻接表,我们不仅仅存储某个节点 x 的所有邻居节点,还存储 x 到每个邻居的权重,不就实现加权有向图了吗?
如果是邻接矩阵,matrix[x][y] 不再是布尔值,而是一个 int 值,0 表示没有连接,其他值表示权重,不就变成加权有向图了吗?
代码实现
// 邻接表
// graph[x] 存储 x 的所有邻居节点以及对应的权重
List<int[]>[] graph;
// 邻接矩阵
// matrix[x][y] 记录 x 指向 y 的边的权重,0 表示不相邻
int[][] matrix;
无向图怎么实现?也很简单,所谓的「无向」,等同于「双向」
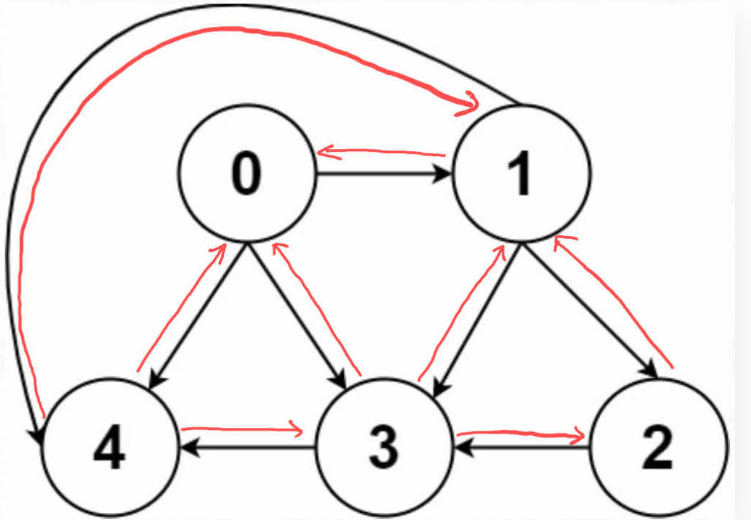
如果连接无向图中的节点 x 和 y,把 matrix[x][y] 和 matrix[y][x] 都变成 true 不就行了;邻接表也是类似的操作,在 x 的邻居列表里添加 y,同时在 y 的邻居列表里添加 x。
遍历
图怎么遍历?还是那句话,参考多叉树
多叉树的 DFS 遍历框架如下:
/* 多叉树遍历框架 */
void traverse(TreeNode root) {
if (root == null) return;
// 前序位置
for (TreeNode child : root.children) {
traverse(child);
}
// 后序位置
}
图和多叉树最大的区别是:图是可能包含环的,你从图的某一个节点开始遍历,有可能走了一圈又回到这个节点,而树不会出现这种情况,从某个节点出发必然走到叶子节点,绝不可能回到它自身。
所以,如果图包含环,遍历框架就要一个 visited 数组进行辅助
// 记录被遍历过的节点
boolean[] visited;
// 记录从起点到当前节点的路径
boolean[] onPath;
/* 图遍历框架 */
void traverse(Graph graph, int s) {
if (visited[s]) return;
// 经过节点 s,标记为已遍历
visited[s] = true;
// 做选择:标记节点 s 在路径上
onPath[s] = true;
for (int neighbor : graph.neighbors(s)) {
traverse(graph, neighbor);
}
// 撤销选择:节点 s 离开路径
onPath[s] = false;
}
广度优先算法(BFS)
BFS 的核心思想应该不难理解的,就是把一些问题抽象成图,从一个点开始,向四周开始扩散。一般来说,我们写 BFS 算法都是用「队列」这种数据结构,每次将一个节点周围的所有节点加入队列
BFS 相对 DFS 的最主要的区别是:BFS 找到的路径一定是最短的,但代价就是空间复杂度可能比 DFS 大很多
框架
// 计算从起点 start 到终点 target 的最近距离
int BFS(Node start, Node target) {
Queue<Node> q; // 核心数据结构
Set<Node> visited; // 避免走回头路
q.offer(start); // 将起点加入队列
visited.add(start);
int step = 0; // 记录扩散的步数
while (q not empty) {
int sz = q.size();
/* 将当前队列中的所有节点向四周扩散 */
for (int i = 0; i < sz; i++) {
Node cur = q.poll();
/* 划重点:这里判断是否到达终点 */
if (cur is target)
return step;
/* 将 cur 的相邻节点加入队列 */
for (Node x : cur.adj()) {
if (x not in visited) {
q.offer(x);
visited.add(x);
}
}
}
/* 划重点:更新步数在这里 */
step++;
}
}
cur.adj() 泛指 cur 相邻的节点,比如说二维数组中,cur 上下左右四面的位置就是相邻节点;visited 的主要作用是防止走回头路,大部分时候都是必须的,但是像一般的二叉树结构,没有子节点到父节点的指针,不会走回头路就不需要 visited。
111. 二叉树的最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
class Solution {
public int minDepth(TreeNode root) {
if (root == null) return 0;
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
// root 本身就是一层,depth 初始化为 1
int depth = 1;
while (!q.isEmpty()) {
int sz = q.size();
/* 将当前队列中的所有节点向四周扩散 */
for (int i = 0; i < sz; i++) {
TreeNode cur = q.poll();
/* 判断是否到达终点 */
if (cur.left == null && cur.right == null)
return depth;
/* 将 cur 的相邻节点加入队列 */
if (cur.left != null)
q.offer(cur.left);
if (cur.right != null)
q.offer(cur.right);
}
/* 这里增加步数 */
depth++;
}
return depth;
}
}
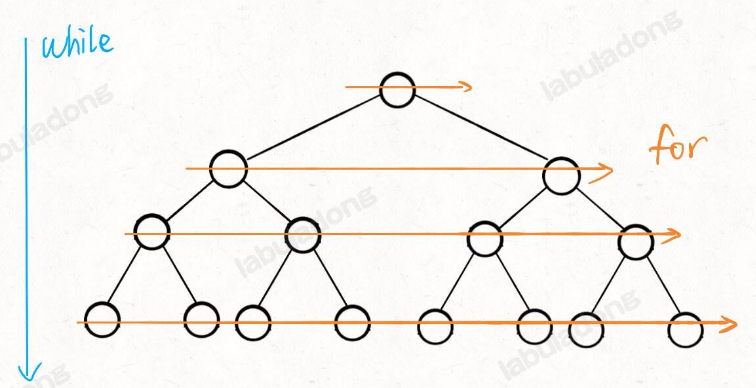
注意这个 while 循环和 for 循环的配合,while 循环控制一层一层往下走,for 循环利用 sz 变量控制从左到右遍历每一层二叉树节点:
752. 打开转盘锁
你有一个带有四个圆形拨轮的转盘锁。每个拨轮都有10个数字: '0', '1', '2', '3', '4', '5', '6', '7', '8', '9' 。每个拨轮可以自由旋转:例如把 '9' 变为 '0','0' 变为 '9' 。每次旋转都只能旋转一个拨轮的一位数字。
锁的初始数字为 '0000' ,一个代表四个拨轮的数字的字符串。
列表 deadends 包含了一组死亡数字,一旦拨轮的数字和列表里的任何一个元素相同,这个锁将会被永久锁定,无法再被旋转。
字符串 target 代表可以解锁的数字,你需要给出解锁需要的最小旋转次数,如果无论如何不能解锁,返回 -1
思路:
1、先穷举所有可能的密码组合了
// 将 s[j] 向上拨动一次
String plusOne(String s, int j) {
char[] ch = s.toCharArray();
if (ch[j] == '9')
ch[j] = '0';
else
ch[j] += 1;
return new String(ch);
}
// 将 s[i] 向下拨动一次
String minusOne(String s, int j) {
char[] ch = s.toCharArray();
if (ch[j] == '0')
ch[j] = '9';
else
ch[j] -= 1;
return new String(ch);
}
// BFS 框架,打印出所有可能的密码
void BFS(String target) {
Queue<String> q = new LinkedList<>();
q.offer("0000");
while (!q.isEmpty()) {
int sz = q.size();
/* 将当前队列中的所有节点向周围扩散 */
for (int i = 0; i < sz; i++) {
String cur = q.poll();
/* 判断是否到达终点 */
System.out.println(cur);
/* 将一个节点的相邻节点加入队列 */
for (int j = 0; j < 4; j++) {
String up = plusOne(cur, j);
String down = minusOne(cur, j);
q.offer(up);
q.offer(down);
}
}
/* 在这里增加步数 */
}
return;
}
有如下问题需要解决:
1、会走回头路。比如说我们从 "0000" 拨到 "1000",但是等从队列拿出 "1000" 时,还会拨出一个 "0000",这样的话会产生死循环。
2、没有终止条件,按照题目要求,我们找到 target 就应该结束并返回拨动的次数。
3、没有对 deadends 的处理,按道理这些「死亡密码」是不能出现的,也就是说你遇到这些密码的时候需要跳过。
class Solution {
public int openLock(String[] deadends, String target) {
// 记录需要跳过的死亡密码
Set<String> deads = new HashSet<>();
for (String s : deadends) deads.add(s);
// 记录已经穷举过的密码,防止走回头路
Set<String> visited = new HashSet<>();
Queue<String> q = new LinkedList<>();
// 从起点开始启动广度优先搜索
int step = 0;
q.offer("0000");
visited.add("0000");
while (!q.isEmpty()) {
int sz = q.size();
/* 将当前队列中的所有节点向周围扩散 */
for (int i = 0; i < sz; i++) {
String cur = q.poll();
/* 判断是否到达终点 */
if (deads.contains(cur))
continue;
if (cur.equals(target))
return step;
/* 将一个节点的未遍历相邻节点加入队列 */
for (int j = 0; j < 4; j++) {
String up = plusOne(cur, j);
if (!visited.contains(up)) {
q.offer(up);
visited.add(up);
}
String down = minusOne(cur, j);
if (!visited.contains(down)) {
q.offer(down);
visited.add(down);
}
}
}
/* 在这里增加步数 */
step++;
}
// 如果穷举完都没找到目标密码,那就是找不到了
return -1;
}
// 将 s[j] 向上拨动一次
private String plusOne(String s, int j) {
char[] ch = s.toCharArray();
if (ch[j] == '9')
ch[j] = '0';
else
ch[j] += 1;
return new String(ch);
}
// 将 s[i] 向下拨动一次
private String minusOne(String s, int j) {
char[] ch = s.toCharArray();
if (ch[j] == '0')
ch[j] = '9';
else
ch[j] -= 1;
return new String(ch);
}
}
773. 滑动谜题
在一个 2 x 3 的板上(board)有 5 块砖瓦,用数字 1~5 来表示, 以及一块空缺用 0 来表示。一次 移动 定义为选择 0 与一个相邻的数字(上下左右)进行交换.
最终当板 board 的结果是 [[1,2,3],[4,5,0]] 谜板被解开。
给出一个谜板的初始状态 board ,返回最少可以通过多少次移动解开谜板,如果不能解开谜板,则返回 -1 。
思考:
1、一般的 BFS 算法,是从一个起点 start 开始,向终点 target 进行寻路,但是拼图问题不是在寻路,而是在不断交换数字,这应该怎么转化成 BFS 算法问题呢?
2、即便这个问题能够转化成 BFS 问题,如何处理起点 start 和终点 target?它们都是数组,把数组放进队列,套 BFS 框架,想想就比较麻烦且低效。
第一个问题,BFS 算法并不只是一个寻路算法,而是一种暴力搜索算法,只要涉及暴力穷举的问题,BFS 就可以用,而且可以最快地找到答案。
我们的问题就转化成了:如何穷举出 board 当前局面下可能衍生出的所有局面?这就简单了,看数字 0 的位置,和上下左右的数字进行交换就行了:
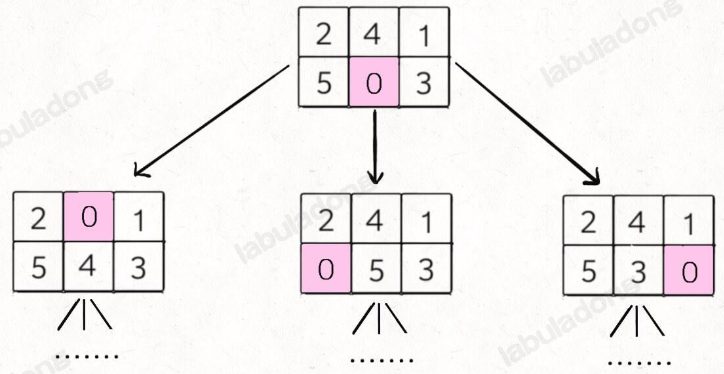
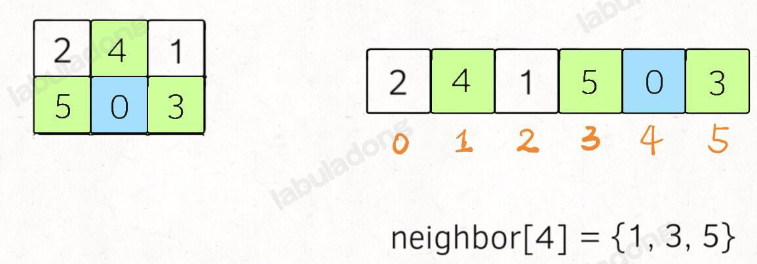
对于第二个问题,我们这里的 board 仅仅是 2x3 的二维数组,所以可以压缩成一个一维字符串。其中比较有技巧性的点在于,二维数组有「上下左右」的概念,压缩成一维后,如何得到某一个索引上下左右的索引?
比如看这个相邻的「下标索引」映射
// 记录一维字符串的相邻索引
int[][] neighbor = new int[][]{
{1, 3},
{0, 4, 2},
{1, 5},
{0, 4},
{3, 1, 5},
{4, 2}
};
含义就是,在一维字符串中,索引 i 在二维数组中的的相邻索引为 neighbor[i]:
class Solution {
public int slidingPuzzle(int[][] board) {
int m = 2, n = 3;
StringBuilder sb = new StringBuilder();
String target = "123450";
// 将 2x3 的数组转化成字符串作为 BFS 的起点
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
sb.append(board[i][j]);
}
}
String start = sb.toString();
// 记录一维字符串的相邻索引
int[][] neighbor = new int[][]{
{1, 3},
{0, 4, 2},
{1, 5},
{0, 4},
{3, 1, 5},
{4, 2}
};
/******* BFS 算法框架开始 *******/
Queue<String> q = new LinkedList<>();
HashSet<String> visited = new HashSet<>();
// 从起点开始 BFS 搜索
q.offer(start);
visited.add(start);
int step = 0;
while (!q.isEmpty()) {
int sz = q.size();
for (int i = 0; i < sz; i++) {
String cur = q.poll();
// 判断是否达到目标局面
if (target.equals(cur)) {
return step;
}
// 找到数字 0 的索引
int idx = 0;
for (; cur.charAt(idx) != '0'; idx++) ;
// 将数字 0 和相邻的数字交换位置
for (int adj : neighbor[idx]) {
String new_board = swap(cur.toCharArray(), adj, idx);
// 防止走回头路
if (!visited.contains(new_board)) {
q.offer(new_board);
visited.add(new_board);
}
}
}
step++;
}
/******* BFS 算法框架结束 *******/
return -1;
}
private String swap(char[] chars, int i, int j) {
char temp = chars[i];
chars[i] = chars[j];
chars[j] = temp;
return new String(chars);
}
}
双向BFS
区别:传统的 BFS 框架就是从起点开始向四周扩散,遇到终点时停止;而双向 BFS 则是从起点和终点同时开始扩散,当两边有交集的时候停止
它俩的最坏复杂度都是 O(N)
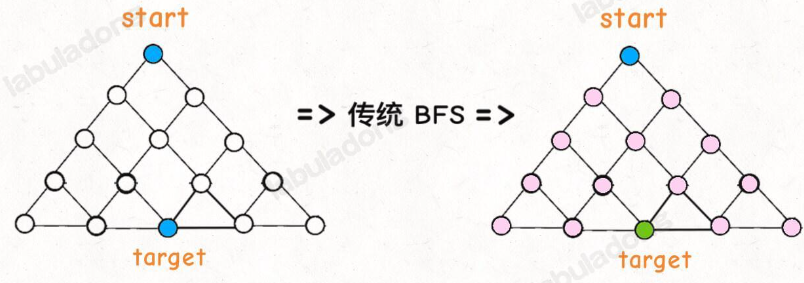
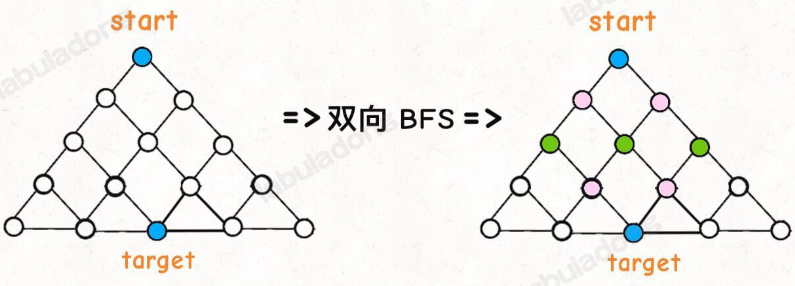
图示中的树形结构,如果终点在最底部,按照传统 BFS 算法的策略,会把整棵树的节点都搜索一遍,最后找到 target;而双向 BFS 其实只遍历了半棵树就出现了交集,也就是找到了最短距离。
不过,双向 BFS 也有局限,因为你必须知道终点在哪里。比如我们刚才讨论的二叉树最小高度的问题,你一开始根本就不知道终点在哪里,也就无法使用双向 BFS;但是第二个密码锁的问题,是可以使用双向 BFS 算法来提高效率的
双向BFS优化
int openLock(String[] deadends, String target) {
Set<String> deads = new HashSet<>();
for (String s : deadends) deads.add(s);
// 用集合不用队列,可以快速判断元素是否存在
Set<String> q1 = new HashSet<>();
Set<String> q2 = new HashSet<>();
Set<String> visited = new HashSet<>();
int step = 0;
q1.add("0000");
q2.add(target);
while (!q1.isEmpty() && !q2.isEmpty()) {
// 哈希集合在遍历的过程中不能修改,用 temp 存储扩散结果
Set<String> temp = new HashSet<>();
/* 将 q1 中的所有节点向周围扩散 */
for (String cur : q1) {
/* 判断是否到达终点 */
if (deads.contains(cur))
continue;
if (q2.contains(cur))
return step;
visited.add(cur);
/* 将一个节点的未遍历相邻节点加入集合 */
for (int j = 0; j < 4; j++) {
String up = plusOne(cur, j);
if (!visited.contains(up))
temp.add(up);
String down = minusOne(cur, j);
if (!visited.contains(down))
temp.add(down);
}
}
/* 在这里增加步数 */
step++;
// temp 相当于 q1
// 这里交换 q1 q2,下一轮 while 就是扩散 q2
q1 = q2;
q2 = temp;
}
return -1;
}
双向 BFS 还是遵循 BFS 算法框架的,只是不再使用队列,而是使用 HashSet 方便快速判断两个集合是否有交集。
另外的一个技巧点就是 while 循环的最后交换 q1 和 q2 的内容,所以只要默认扩散 q1 就相当于轮流扩散 q1 和 q2。
其实双向 BFS 还有一个优化,就是在 while 循环开始时做一个判断
深度优先算法(DFS)
其实 DFS 算法就是回溯算法
回溯算法和 DFS 算法的细微差别是:回溯算法是在遍历「树枝」,DFS 算法是在遍历「节点」
797. 所有可能的路径
给你一个有 n 个节点的 有向无环图(DAG),请你找出所有从节点 0 到节点 n-1 的路径并输出(不要求按特定顺序)
graph[i] 是一个从节点 i 可以访问的所有节点的列表(即从节点 i 到节点 graph[i][j]存在一条有向边)。
解法很简单,以 0 为起点遍历图,同时记录遍历过的路径,当遍历到终点时将路径记录下来即可。
既然输入的图是无环的,我们就不需要 visited 数组辅助了,直接套用图的遍历框架
class Solution {
// 记录所有路径
List<List<Integer>> res = new LinkedList<>();
public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
// 维护递归过程中经过的路径
LinkedList<Integer> path = new LinkedList<>();
traverse(graph, 0, path);
return res;
}
/* 图的遍历框架 */
private void traverse(int[][] graph, int s, LinkedList<Integer> path) {
// 添加节点 s 到路径
path.addLast(s);
int n = graph.length;
if (s == n - 1){
// 到达终点
res.add(new LinkedList<>(path));
// 可以在这直接 return,但要 removeLast 正确维护 path
// path.removeLast();
// return;
// 不 return 也可以,因为图中不包含环,不会出现无限递归
}
// 递归每个相邻节点
for (int v : graph[s]) {
traverse(graph, v, path);
}
// 从路径移出节点 s
path.removeLast();
}
}
–end–