1.加法原理:

完成一个工程可以有n类办法，a[i](1<=i<=n) 代表第i类方法的数目。

那么完成这件事共有  S = a[1]+a[2]+...+a[n]种不同的方法。 

2.乘法原理:

完成一个工程需要分n个步骤，a[i](1<=i<=n) 代表第i个步骤的不同方法数目。

那么完成这件事共有 S = a[1]*a[2]*...*a[n]种不同的方法。 

3.两个原理的区别:

加法原理：分类完成，每个方法是独立的。

乘法原理：分步完成，步与步是连续地，依次相继完成。

  

   4、捆绑与插空:

    例题：4人排成一队，甲和乙必须相邻，有多少种排队方法？

    【答案与分析】把甲乙捆绑，和另外两人排列。P(3,3)*2=12。

     例题：某人射击8枪，命中4枪，恰好有3枪连续命中，有多少种不同的情况？

    【答案与分析】20。

分析：因为连续命中的三枪与单独命中的一枪不能相邻，因而这是一个插空问题。另外没有命中的之间没有区别，不必计数。即在四发空枪之间形成的5个空中选出2个的排列，即 P(5,2)。

    5、环形排列

    n 个人围成一圈，不同的排列方式有P(n-1,n-1)种。

  对于可以翻转的环形排列，还应该除以2.

 

组合

同样还是颁奖，这次我们颁的不是金、银、铜牌，而是 3 个一模一样的可乐瓶，所以给谁先颁奖后颁奖，结果都是一样的，Alice 先颁发到一个可乐瓶、Bob 后拿到，跟 Bob先拿到一个可乐瓶、Alice后拿到，两种结果都是一样的。

那么在 8 个人当中选 3 个人颁发一样的可乐瓶，有多少种颁发方法呢？

所以，我们只需要把「上一步排列获得的结果」除以「不同颁发顺序的总数」，得到的就是可乐瓶颁发方法的总数。

不同颁发顺序的总数有 3！种

所以，总共有这么多种：

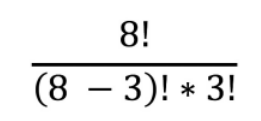
如果要想在 n 个物品中，选择 k 个物品出来，选择的顺序无所谓，那么选择的方式总共有这么多种：

排列称为 P。组合称为 C。

P 和 C 的本质区别在于：决策的顺序对结果有没有影响。

下面举例说明

现在有8个人，他们的名字分别为：

 Alice

Bob

Catherine

Donald

Elizabeth

Floria

Gates

00008. Hinton

现在有 3 个奖杯，本别为 Golden 金牌，Silver 银牌，Bronze 铜牌。

我们的任务是：将这 3 个奖牌颁发给 8 个人中的 3 个，先颁发金牌，再颁发银牌，再颁发铜牌。这是一个排列的问题，因为把金牌先颁给 Alice，再把银牌颁给 Bob，跟把金牌先颁给 Bob，再把银牌颁给 Alice 这是两种不同的颁奖方式。

好了，现在假设我们先把金牌颁发给 Alice，再把银牌颁发给 Bob，再把铜牌颁发给 Catherine：

第一步：颁发金牌 ️，可以在8个人中任选一个，有8种选择。A可以被替换为 B C D E F G H中的任何一个。

第二步：颁发银牌 ，可以在除去已经获得金牌的人之外的7个人中任选一个，有7种选择。

第三步：颁发铜牌 ，在已经获得金牌、银牌的两个人之外的6个人中任选一个，有6种选择。

那么很明显，总共的颁奖方式有

8 * 7 * 6 种

以此类推，假如我们现在要颁发 8 个奖牌给 8个人，那么我们会按照上述方法，每次颁发一种奖牌，直到奖牌被颁发完为止，这样，颁发奖牌的方式总共有：

8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 种

但是，我们只颁发 3 个奖牌就不颁发了，所以等于

也就是：

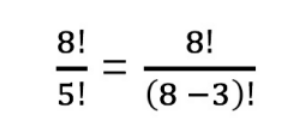
如果我们现在有 n 个运动员，要按顺序地颁发 k 个奖牌，有多少不同的颁奖方式呢？答案是：

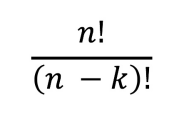
如果要想在 n 个物品中，按顺序的选择 k 个物品，那么选择的方式总共有这么多种：